Unterstützt JavaScript trigonometrische Funktionen?

JavaScript unterstützt trigonometrische Funktionen. Trigonometrische Funktionen in js sind alle statische Methoden und müssen mit Mathe aufgerufen werden, daher ist das Syntaxformat „Math.sin(x)“, „Math.cos(x)“, „Math.tan(x)“.

Die Betriebsumgebung dieses Tutorials: Windows 7-System, JavaScript-Version 1.8.5, Dell G3-Computer.

JavaScript unterstützt trigonometrische Funktionen. Sie sind: „Math.sin(x)“, „Math.cos(x)“, „Math.tan(x)“.

Werfen wir einen Blick auf die JavaScript-Unterstützung für trigonometrische Funktionen.

Lassen Sie uns zunächst die Grundkenntnisse der trigonometrischen Funktionen überprüfen, die wir in der High School gelernt haben. Die erste ist die Sin-Funktion, die zweite ist die Cos-Funktion und die dritte ist die Tan Die Funktion „Vier“ oder „Vier“ ist in der Mathematik der Wert, den man durch den Vergleich der gegenüberliegenden Seiten eines Dreiecks mit der Hypotenuse erhält.

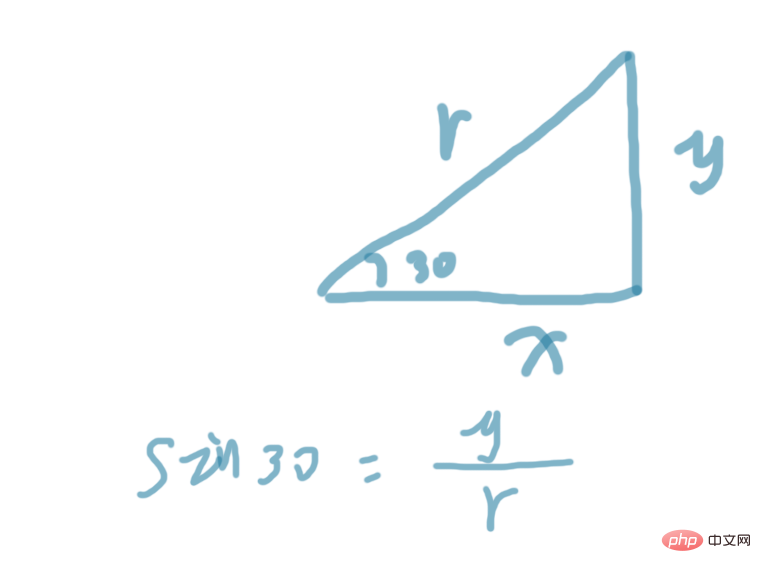
x/r code>, die cos-Funktion ist das Verhältnis der gegenüberliegenden Seite zur oberen Seite, tan30=y/x, und die tan-Funktion ist das Verhältnis der gegenüberliegenden Seite zur oberen Seite Durch diese Formeln können wir leicht die Werte dieser trigonometrischen Funktion erhalten und diese Werte dann verwenden, um interessante Dinge zu tun! ! cos30=x/r，cos函数是临边比上斜边，tan30=y/x，tan函数则是对边比上临边，通过这些公式，我们可以很容易的得到这个三角函数的值，然后就阔以拿这些值去做有意思的事情啦！！

那么我们在javascript里面的三角函数和数学中的三角函数其实有一点区别外，第一是写发上不一样，js里面三角函数都是静态方法，必须使用Math来调用，三个函数分别是Math.sin()，Math.cos()，Math.tan()。

这个很容易理解咯，那么第二个不同就是数学里面的三角函数使用接受的参数是角度，但是在js里面所接受的参数是弧度，有的朋友可能晕了，弧度角度什么玩意？？？不要着急，这里简单介绍一下，我们首先来看一个圆

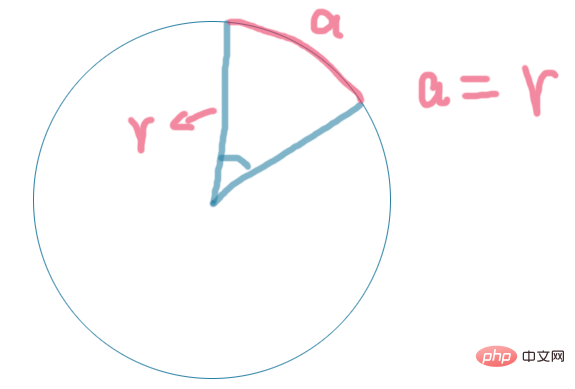
如果一个圆的一段边的长度等于这个圆的半径长度，那么这段边就代表一弧度，正如图中红色部分，就代表一弧度，这个其实仅仅就是一个概念，我们真正要使用的是吧我们想要的角度转化成弧度，这里直接套用数学公公式  1角度=π/180  那么10个角度就等于10*π/180啦

那我们要用js的Math.sin()算出30度角等于多少，那么就应该写成Math.sin(30*Math.PI/180)，这里注意一下js里面的π是Math.PI

Dann gibt es tatsächlich einige Unterschiede zwischen unseren trigonometrischen Funktionen in JavaScript und den trigonometrischen Funktionen in der Mathematik. Der erste besteht darin, dass die trigonometrischen Funktionen in js alle statische Methoden sind und mit Mathe aufgerufen werden müssen Es ist Math.sin(), Math.cos(), Math.tan().

Der zweite Unterschied besteht darin, dass die von trigonometrischen Funktionen in der Mathematik akzeptierten Parameter das Bogenmaß sind. Einige Freunde sind möglicherweise verwirrt. ? ? Keine Sorge, hier ist eine kurze Einführung. Schauen wir uns zunächst einen Kreis an. alt=" "/>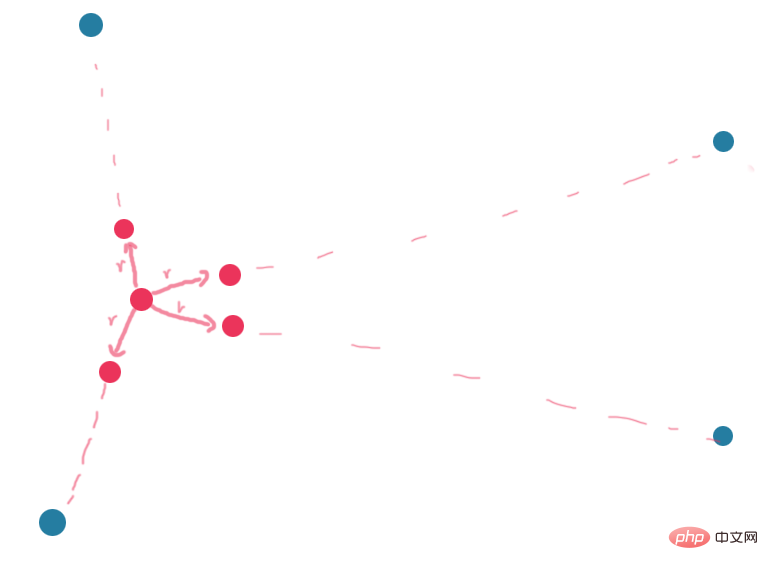

Wenn die Länge einer Seite eines Kreises gleich dem Radius des Kreises ist, stellt diese Seite genau wie der rote Teil im Bild ein Bogenmaß dar nur ein Konzept. Was wir wirklich wollen, ist, den gewünschten Winkel in Bogenmaß umzurechnen. Hier wenden wir direkt die mathematische Formel 1 Winkel=π/180 an. Dann sind 10 Winkel gleich 10*π/180 La

Dann müssen wir Math.sin() von js verwenden, um den Winkel von 30 Grad zu berechnen, dann sollte er als Math.sin geschrieben werden (30*Math.PI/180), bitte beachten Sie hier, dass π in js Math.PI ist. Ich glaube, dass hier jeder ein gewisses Verständnis für die trigonometrischen Funktionen von js haben muss. Schauen wir uns also ein kleines praktisches Beispiel an.

　Zuallererst gibt es einen Bedarf. Auf der Seite befindet sich eine kleine Kugel. Ich möchte, dass sich meine Maus dorthin bewegt, wenn sie auf der Seite platziert wird. Der Ball bewegt sich nicht an die entsprechende Position, sondern an die entsprechende Position. Es ist nicht einfach, die URL hier zu posten.

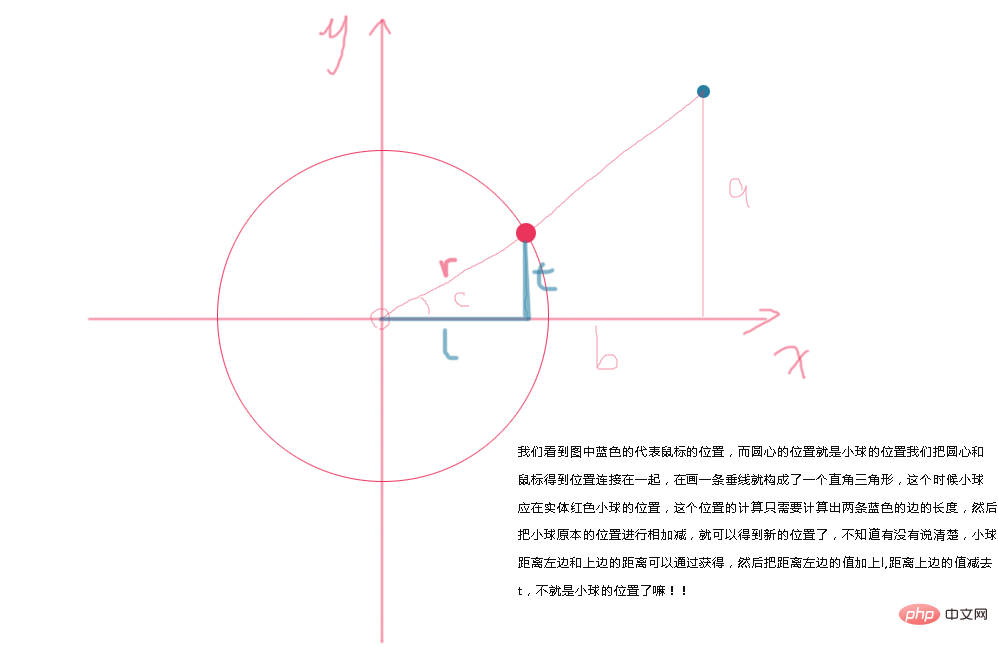
Unter ihnen stellt der rote Ball einen Maulkorb dar. Der blaue Ball stellt die Position der Maus dar. Wenn die Maus an verschiedenen Positionen auf der Seite platziert wird, bewegt sich der rote Ball in den entsprechenden Winkel, aber wir sehen auch, dass es ein r gibt, das den Bereich der Ebene anzeigt , die Reichweite, die sich der rote Ball bewegen kann, entspricht tatsächlich dem Radius eines Kreises. Je größer r ist, desto größer ist die Reichweite, die sich der Ball bewegen kann! ! (Für diejenigen, die es nicht verstehen, kopieren Sie einfach das folgende Beispiel und führen Sie es zuerst aus.)

Die Implementierung dieser Funktion erfordert, dass wir trigonometrische Funktionen verwenden, um die Position der Maus zu erkennen und sie in einem 360-Grad-Bereich zu erkennen. Hier müssen wir den Abstand nach links und den Abstand zur Spitze des roten Balls durch den Winkel berechnen und sie dann dem Ball zuordnen! ! Schauen wir uns ein weiteres Bild an

🎜Das Folgende ist der Code dieses Falls, Freunde, die interessiert sind, können einen Blick darauf werfen! 🎜🎜

/***********例子来了*************/
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd">
<html>
<head>
<meta http-equiv="Content-Type" content="text/html;charset=UTF-8">
<title>Document</title>
<style>
#box{width:30px;height:30px;background:red;position:absolute;top:400px;left:400px;border-radius:15px;}
</style>
</head>
<body>
<p id="box"></p>
</body>
<script>
var obox = document.getElementById(&#39;box&#39;);
var r=50;
document.onmousemove=function(ev){
var oev = ev||event;
var x = Math.abs(oev.clientX-obox.offsetLeft);
var y = Math.abs(oev.clientY-obox.offsetTop);
var angle = Math.atan(y/x);
var cx=0;
var cy=0;
if(oev.clientX>=obox.offsetLeft && oev.clientY<=obox.offsetTop){
cx = Math.cos(angle)*r;
cy = Math.sin(angle)*-r;
}
if(oev.clientX<obox.offsetLeft && oev.clientY<obox.offsetTop){
cx = Math.cos(angle)*-r;
cy = Math.sin(angle)*-r;
}
if(oev.clientX<obox.offsetLeft && oev.clientY>obox.offsetTop){
cx = Math.cos(angle)*-r;
cy = Math.sin(angle)*r;
}
if(oev.clientX>obox.offsetLeft && oev.clientY>obox.offsetTop){
cx = Math.cos(angle)*r;
cy = Math.sin(angle)*r;
}
    obox.style.top = 400+cy+&#39;px&#39;;
obox.style.left = 400+cx+&#39;px&#39;;
}
</script>
</html>

🎜【Empfohlenes Lernen: 🎜Javascript-Tutorial für Fortgeschrittene🎜】🎜

Das obige ist der detaillierte Inhalt vonUnterstützt JavaScript trigonometrische Funktionen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!