Verstehen Sie endlich, dass der MySQL-Index B+tree verwenden muss und dass er so schnell ist

In der Spalte „MySQL-Tutorial“ wird der B+Baum zum Verständnis von Indizes vorgestellt.

Kostenlose Empfehlung:

MySQL-Tutorial(Video)Vorwort

Wenn Sie auf ein langsames SQL stoßen und es optimieren müssen, sollten Sie dies sofort tun Welche Optimierungsmethoden fallen Ihnen ein?

Die erste Reaktion der meisten Leute könnte sein,

einen Index hinzuzufügenSQL 需要进行优化时，你第一时间能想到的优化手段是什么？

大部分人第一反应可能都是添加索引，在大多数情况下面，索引能够将一条 SQL 语句的查询效率提高几个数量级。

索引的本质：用于快速查找记录的一种数据结构。

索引的常用数据结构：

1. 二叉树
2. 红黑树
3. Hash 表
4. B-tree （B树，并不叫什么B减树）
5. B+tree

数据结构图形化网址：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

索引查询

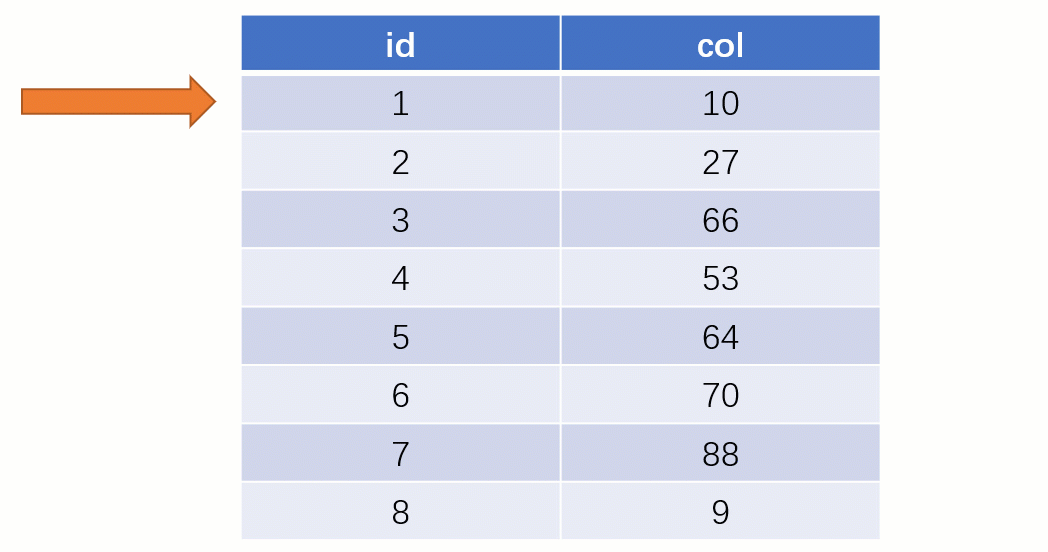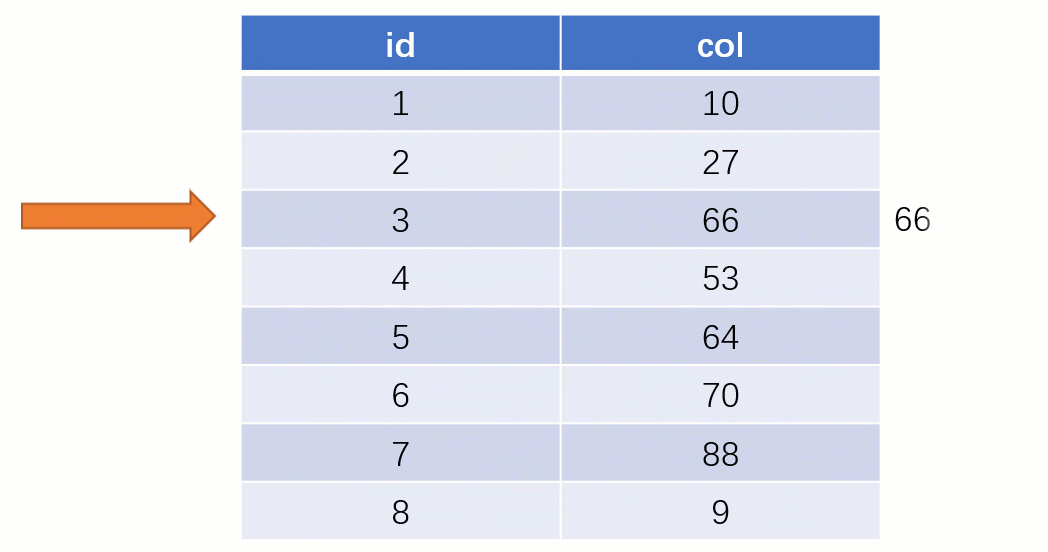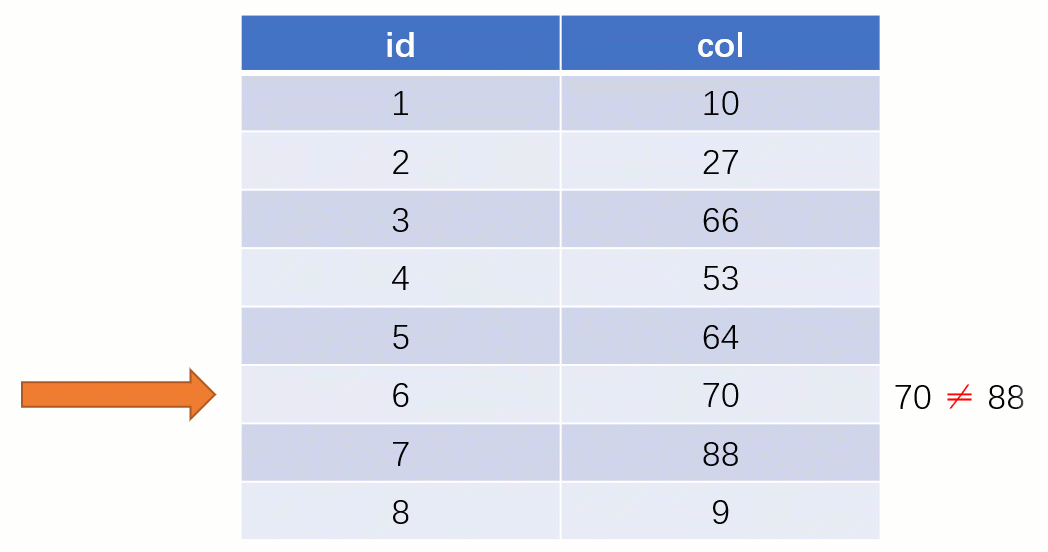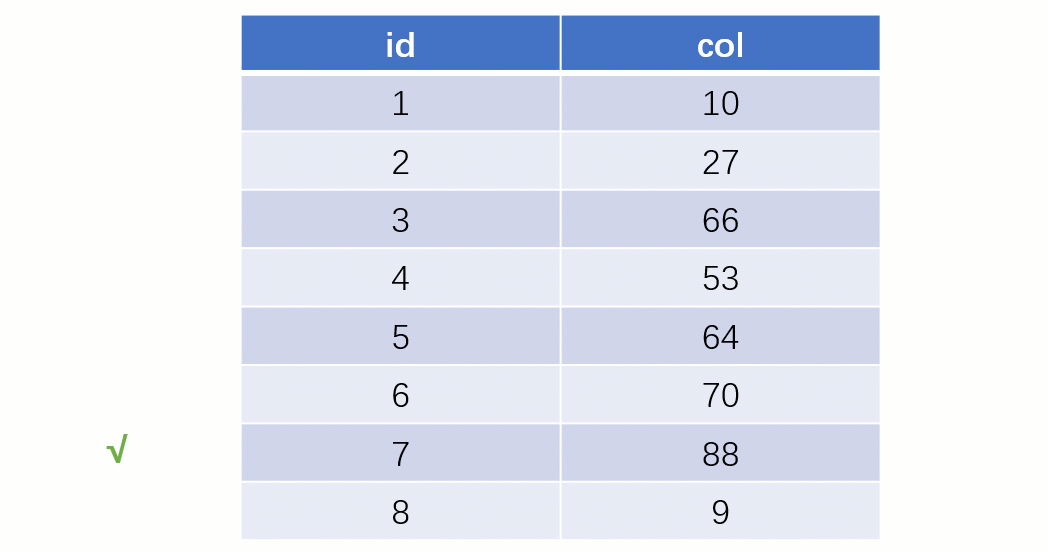
大家知道 select * from t where col = 88 这么一条 SQL 语句如果不走索引进行查找的话，正常地查就是全表扫描：从表的第一行记录开始逐行找，把每一行的 col 字段的值和 88 进行对比，这明显效率是很低的。

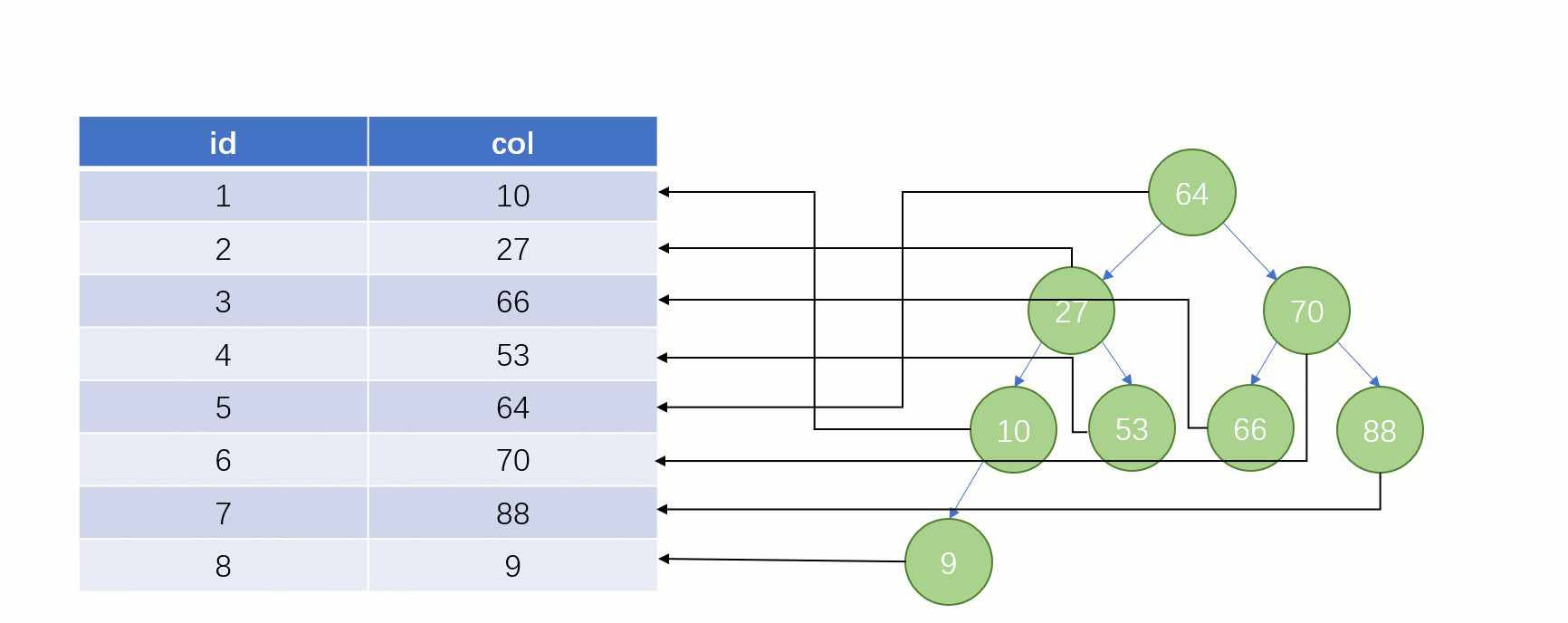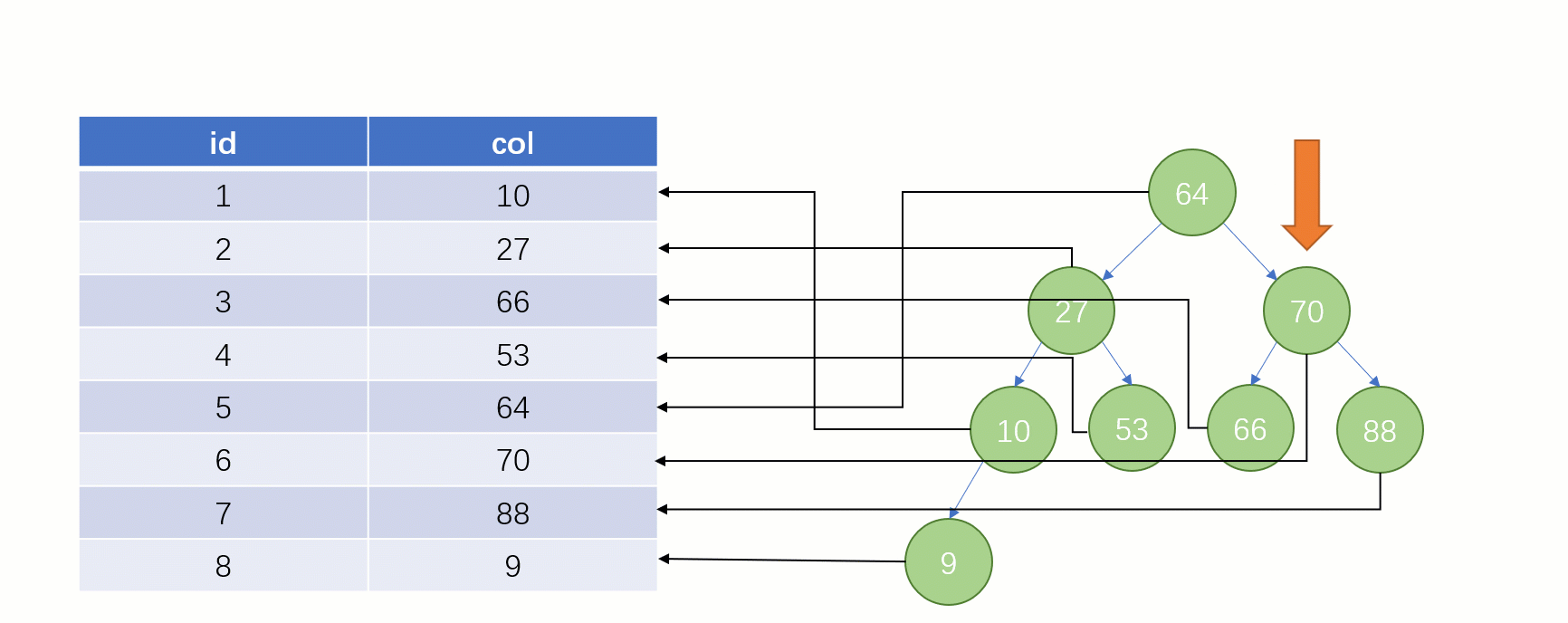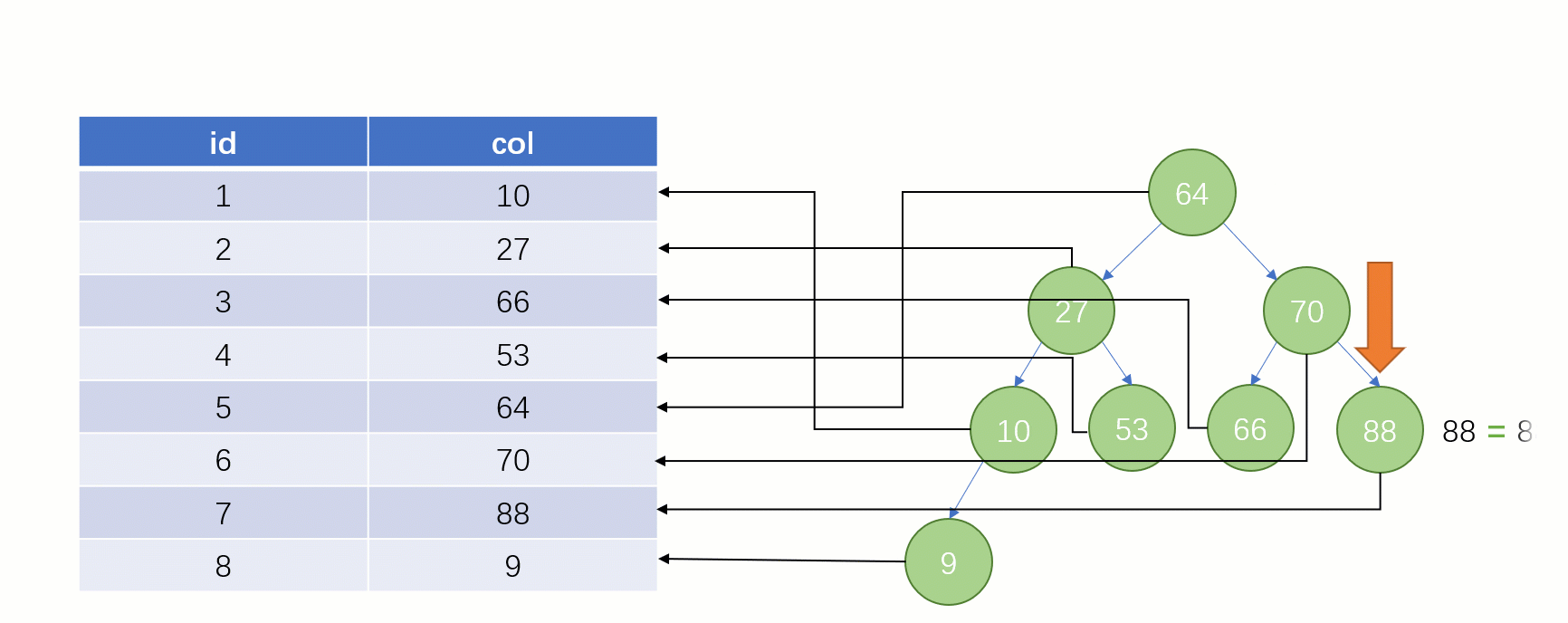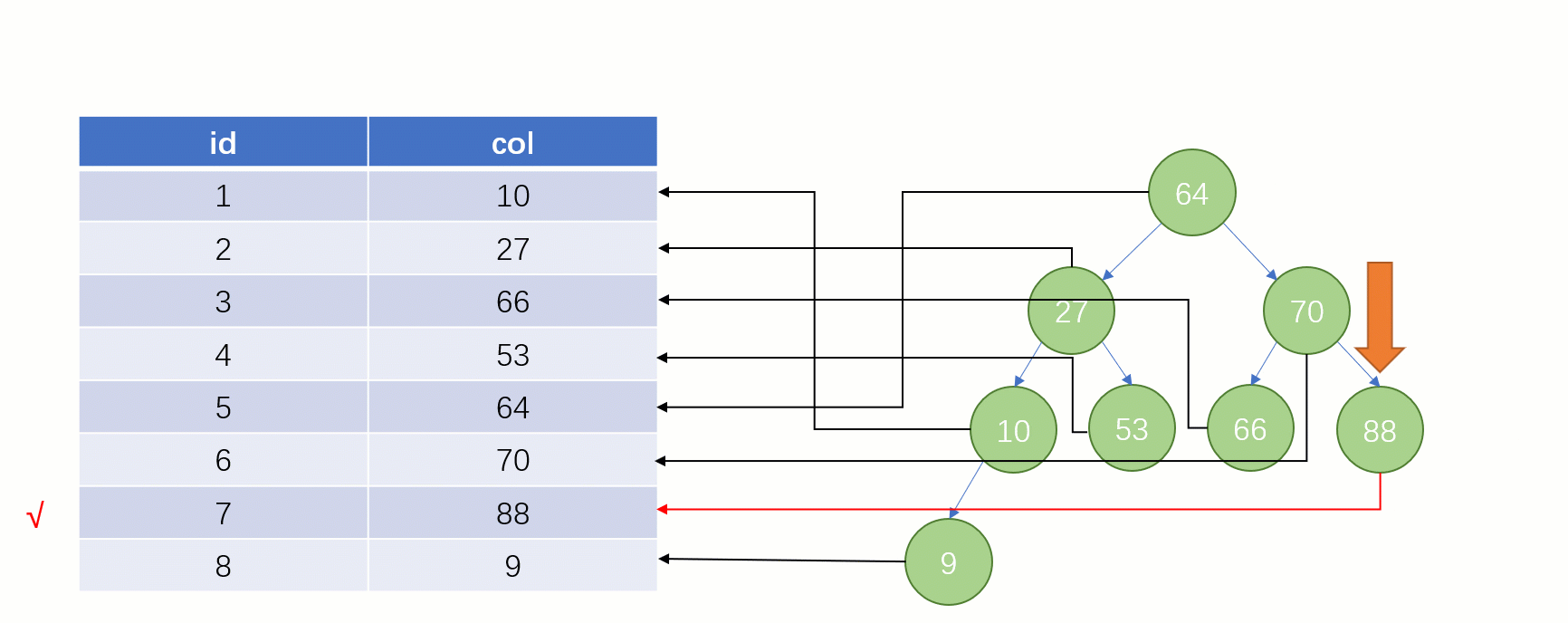
而如果走索引的话，查询的流程就完全不一样了（假设现在用一棵平衡二叉树数据结构存储我们的索引列）

此时该二叉树的存储结构（Key - Value）：Key 就是索引字段的数据，Value 就是索引所在行的磁盘文件地址。

当最后找到了 88 的时候，就可以把它的 Value 对应的磁盘文件地址拿出来，然后就直接去磁盘上去找这一行的数据，这时候的速度就会比全表扫描要快很多。

但实际上 MySQL 底层并没有用二叉树来存储索引数据，是用的 B+tree（B+树）。

为什么不采用二叉树

假设此时用普通二叉树记录 id 索引列，我们在每插入一行记录的同时还要维护二叉树索引字段。

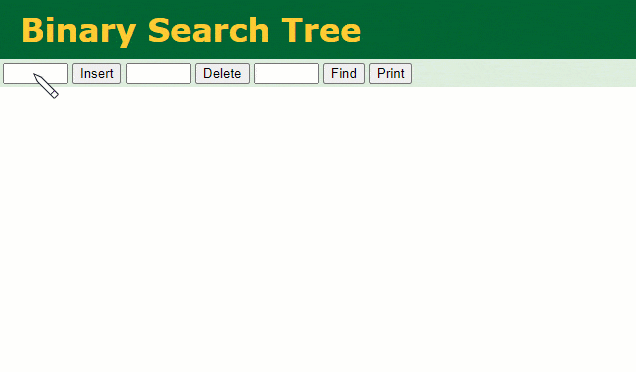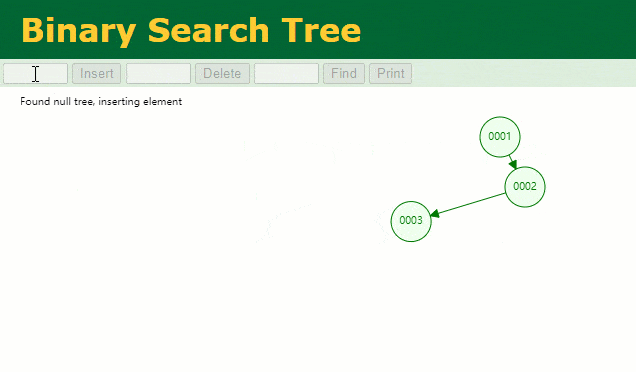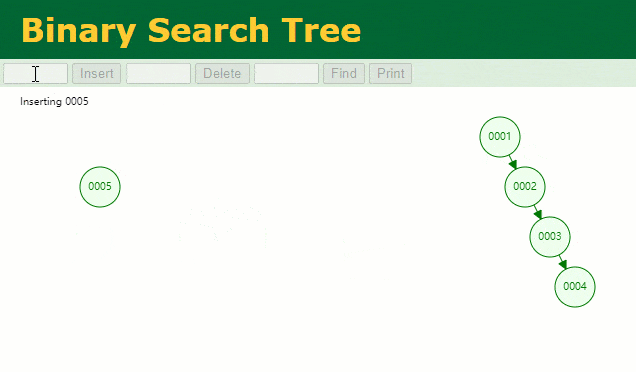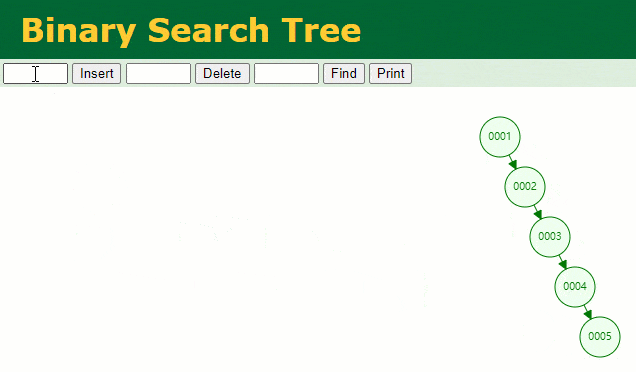
此时当我要找 id = 7 的那条数据时，它的查找过程如下：

此时找 id = 7 这一行记录时找了 7 次，和我们全表扫描也没什么很大区别。显而易见，二叉树对于这种依次递增的数据列其实是不适合作为索引的数据结构。

为什么不采用 Hash 表

Hash 表：一个快速搜索的数据结构，搜索的时间复杂度 O(1)

Hash 函数：将一个任意类型的 key，可以转换成一个 int 类型的下标

假设此时用 Hash 表记录 id 索引列，我们在每插入一行记录的同时还要维护 Hash 表索引字段。

这时候开始查找 id = 7 的树节点仅找了 1 次，效率非常高了。

但 MySQL In den meisten Fällen kann Index die Abfrageeffizienz einer SQL-Anweisung um mehrere Größenordnungen verbessern. Das Wesen eines Index: eine

Datenstruktur

, die zum schnellen Auffinden von Datensätzen verwendet wird.

Häufig verwendete

Datenstrukturen

für Indizes:

1. Binärbaum
2. Rot-Schwarz-Baum
3. Hash-Tabelle
4. B-Baum (B-Baum wird nicht B-subtrahierter Baum genannt)
5. B+Baum

🎜Grafische Datenstruktur🎜 Website: https://www.cs.usfca.edu/~galles/visualization/Algorithms.html🎜

Indexabfrage🎜🎜Jeder weiß esselect * from t where col = 88 Wenn eine solche SQL-Anweisung ohne Verwendung eines Index durchsucht wird, ist die normale Suche ein 🎜vollständiger Tabellenscan🎜: Beginnend mit der ersten Zeile der Tabelle, Suche Zeile für Zeile, und das Durchsuchen des col jeder Zeile mit 🎜88🎜, das ist offensichtlich sehr ineffizient. 🎜🎜🎜🎜Wenn Sie einen Index verwenden, ist der Abfrageprozess völlig anders (vorausgesetzt, dass eine 🎜ausgeglichene Binärbaum-Datenstruktur zum Speichern unserer Indexspalten verwendet wird)🎜🎜Dies Speicherstruktur des Binärbaums (Schlüssel – Wert): Schlüssel sind die Daten des Indexfelds und Wert ist die Festplattendateiadresse der Zeile, in der sich der Index befindet. 🎜🎜Wenn Sie endlich 🎜88🎜 finden, können Sie die dem Wert entsprechende Festplattendateiadresse herausnehmen und dann direkt zur Festplatte gehen, um diese Datenzeile zu finden. Zu diesem Zeitpunkt ist die Geschwindigkeit schneller als bei einer vollständigen Tabelle scanne viel. 🎜🎜Warum nicht einen Binärbaum verwenden? 🎜🎜 Angenommen, ein normaler Binärbaum wird zum Aufzeichnen der Indexspalte id verwendet Index beim Einfügen einer Zeile mit Datensätzen. 🎜🎜🎜🎜Wenn ich die Daten mit id = 7 finden möchte, ist der Suchvorgang wie folgt: 🎜🎜🎜🎜Zu diesem Zeitpunkt haben wir 🎜7🎜 Mal nach dem Zeilendatensatz id = 7 gesucht, was sich nicht wesentlich von unserem vollständigen Tabellenscan unterscheidet. Offensichtlich ist der Binärbaum tatsächlich 🎜 nicht geeignet 🎜 als Indexdatenstruktur für diese Art von 🎜zunehmend 🎜Datenspalten. 🎜

Warum nicht die Hash-Tabelle verwenden🎜🎜🎜Hash-Tabelle: eine Datenstruktur für die schnelle Suche, die Komplexität der Suchzeit beträgt O(1)🎜🎜Hash-Funktion: Konvertieren eines Schlüssels eines beliebigen Typs , kann in einen Index vom Typ int konvertiert werden 🎜

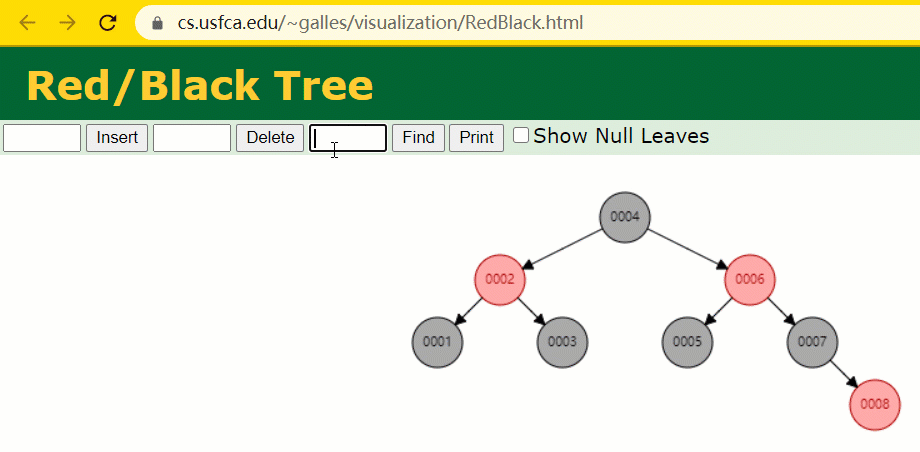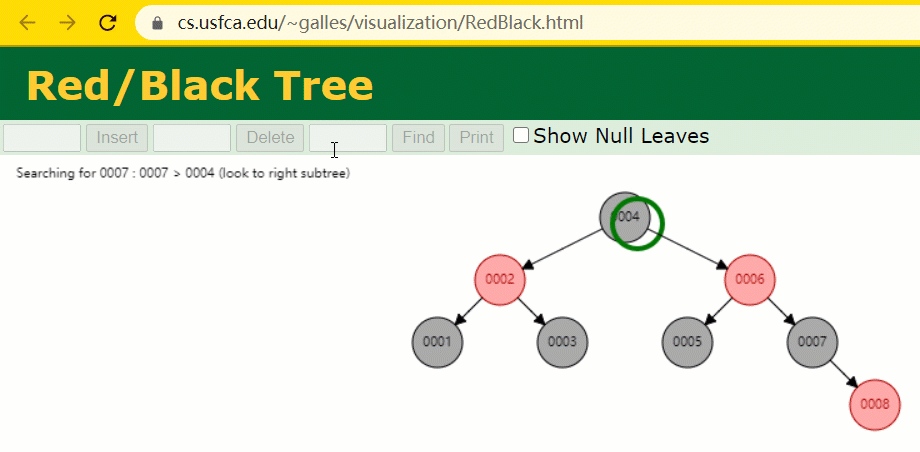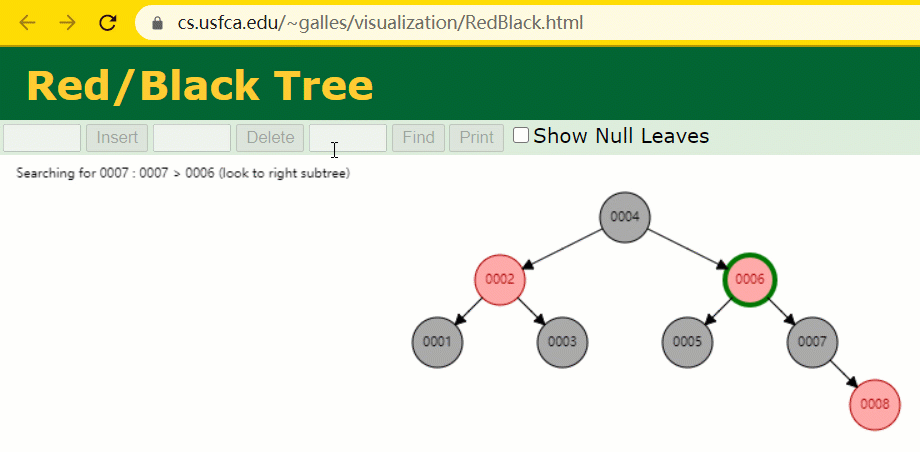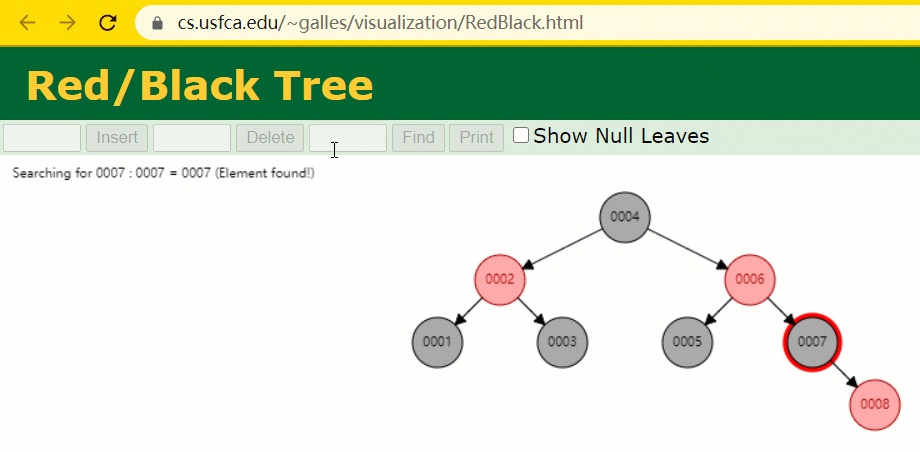
🎜 Unter der Annahme, dass die Hash-Tabelle zum Aufzeichnen der Indexspalte id verwendet wird, müssen wir das Indexfeld der Hash-Tabelle beibehalten, während wir eine Zeile mit Datensätzen einfügen . . 🎜🎜🎜🎜Zu diesem Zeitpunkt wurde der Baumknoten mit id = 7 nur 🎜1🎜 Mal durchsucht, was sehr effizient ist. 🎜🎜🎜🎜Aber der Index von MySQL 🎜verwendet immer noch nicht die 🎜Hash-Tabelle🎜, die genau positioniert werden kann. Weil es 🎜 nicht auf 🎜 Bereichsabfragen 🎜 zutrifft 🎜. 🎜🎜Warum nicht den Rot-Schwarz-Baum verwenden? Der Rot-Schwarz-Baum ist ein spezialisierter AVL-Baum (Balanced Binary Tree), der bestimmte Operationen verwendet, um das Gleichgewicht des binären Suchbaums während Einfüge- und Löschvorgängen aufrechtzuerhalten Wenn ein binärer Suchbaum ein rot-schwarzer Baum ist, muss jeder seiner Teilbäume ein rot-schwarzer Baum sein. 🎜

Unter der Annahme, dass die Indexspalte id zu diesem Zeitpunkt mithilfe eines rot-schwarzen Baums aufgezeichnet wird, müssen wir das Indexfeld des rot-schwarzen Baums beibehalten, während wir eine Zeile mit Datensätzen einfügen. id 索引列，我们在每插入一行记录的同时还要维护红黑树索引字段。

插入过程中会发现它与普通二叉树不同的是当一棵树的左右子树高度差 > 1 时，它会进行自旋操作，保持树的平衡。

这时候开始查找 id = 7 的树节点只找了 3 次，比所谓的普通二叉树还是要更快的。

但 MySQL 的索引依然不采用能够精确定位和范围查询都优秀的红黑树。

因为当 MySQL 数据量很大的时候，索引的体积也会很大，可能内存放不下，所以需要从磁盘上进行相关读写，如果树的层级太高，则读写磁盘的次数（I/O交互）就会越多，性能就会越差。

B-tree

红黑树目前的唯一不足点就是树的高度不可控，所以现在我们的切入点就是树的高度。

目前一个节点是只分配了一个存储 1 个元素，如果要控制高度，我们就可以把一个节点分配的空间更大一点，让它横向存储多个元素，这个时候高度就可控了。这么个改造过程，就变成了 B-tree。

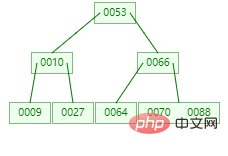
B-tree 是一颗绝对平衡的多路树。它的结构中还有两个概念

度（Degree）：一个节点拥有的子节点（子树）的数量。（有的地方是以度来说明 B-tree 的，这里解释一下）

阶（order）：一个节点的子节点的最大个数。（通常用 m 表示）

关键字：数据索引。

一棵 m 阶 B-tree

1. Während des Einfügevorgangs werden Sie feststellen, dass es sich von gewöhnlichen Binärbäumen dadurch unterscheidet, dass, wenn der Höhenunterschied zwischen dem linken und rechten Teilbaum eines Baums > 1 ist, Es dreht sich, um den Baum im Gleichgewicht zu halten.

   Zu diesem Zeitpunkt wurde der Baumknoten mit id = 7 nur 3 Mal durchsucht, was immer noch schneller ist als der sogenannte gewöhnliche Binärbaum. $$MySQL verwendet immer noch nicht Rot und Schwarz, was eine hervorragende Genauigkeit bietet Positionierungs- und Bereichsabfragebaum. Denn wenn MySQL über eine große Datenmenge verfügt, ist auch die Indexgröße sehr groß und wird möglicherweise nicht im Speicher gespeichert, sodass entsprechende Lese- und Schreibvorgänge von der Festplatte durchgeführt werden müssen Die Ebene des Baums ist zu hoch. Je öfter Sie auf die Festplatte lesen und schreiben (E/A-Interaktionen), desto schlechter wird die Leistung.

   B-Baum

   Der einzige Nachteil des rot-schwarzen Baumes besteht darin, dass die Höhe des Baumes nicht kontrollierbar ist, also jetzt unser Eintrag PunktEs ist die Höhe des Baumes. Derzeit ist einem Knoten nur die Speicherung eines Elements zugewiesen. Wenn wir die Höhe steuern möchten, können wir einem Knoten einen größeren Platz zuweisen und ihn zu diesem Zeitpunkt horizontal speichern Höhe ist steuerbar. Durch diesen Transformationsprozess wurde es zum B-Baum. B-tree ist ein absolut ausgewogener Mehrwegebaum. In seiner Struktur gibt es zwei Konzepte

   Grad: Die Anzahl der untergeordneten Knoten (Teilbäume), die ein Knoten hat. (An manchen Stellen wird B-Baum in Bezug auf Grad erklärt, erklären Sie es hier)

   Ordnung: die maximale Anzahl untergeordneter Knoten eines Knotens. (Normalerweise dargestellt durch m) Schlüsselwort: Datenindex.
   🎜🎜🎜 🎜🎜🎜m 🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜⌉🎜🎜🎜🎜🎜 untergeordneter Knoten; 🎜

   $lceil dfrac{m}{2}rceil$ ist m/2 Runden Sie dann auf

2. Die Anzahl der in jedem Nicht-Root-Knoten enthaltenen Schlüsselwörter j erfüllt: l ceil dfrac{ m }{2}rceil${\displaystyle \frac{}{\mathrm{}}}$2Rudolf Bayer und Ed M. McCreight im Jahr 1972 B-tree wurden während ihrer Arbeit bei Boeing Research Labs erfunden , aber sie erklärten nicht, wofür das B stand (wenn überhaupt).

   Douglas Comer erklärt: Keiner der beiden Autoren hat jemals die ursprüngliche Bedeutung von B-tree erklärt. Wir denken vielleicht, dass eine ausgewogene, breite oder buschige Sorte geeignet sein könnte. Andere meinten, der Buchstabe B stünde für Boeing. Aufgrund seines Sponsorings erscheint es jedoch angemessener, B-Baum als Bayer-Baum zu betrachten.
3. Donald Knuth spekulierte in seinem im Mai 1980 veröffentlichten Artikel mit dem Titel „CS144C-Klassenzimmervorlesung über Festplattenspeicher und B-Trees“ über die Bedeutung des Namens B-tree und deutete an, dass B Boeing oder Bayer bedeuten könnte Name.

   Suchen

B-Baum Die Suche ist tatsächlich einem Binärbaum sehr ähnlich:

4. Ein Binärbaum hat ein Schlüsselwort und jeweils zwei Zweige Knoten: Jeder Knoten im B-Baum hat k Schlüsselwörter und (k + 1) Zweige.

Bei der binären Baumsuche wird nur berücksichtigt, ob nach links oder rechts gegangen werden soll, während B-Baum durch mehrere Zweige bestimmt werden muss.

Die Suche nach B-tree gliedert sich in zwei Schritte:

1. Erste Suche nach Knoten. Da B-tree normalerweise auf der Festplatte gespeichert ist, ist für diesen Schritt ein <strong>Festplatten-IO</strong>-Vorgang erforderlich. <code>B-tree 通常是在磁盘上存储的所以这步需要进行磁盘IO操作；
2. 查找关键字，当找到某个节点后将该节点读入内存中然后通过顺序或者折半查找来查找关键字。若没有找到关键字，则需要判断大小来找到合适的分支继续查找。

操作流程

现在需要查找元素：88

第一次：磁盘IO

第二次：磁盘IO

第三次：磁盘IO

然后这有一次内存比对，分别跟 70 与 88 比对，最后找到 88。

从查找过程中发现，B-tree 比对次数和磁盘IO的次数其实和二叉树相差不了多少，这么看来并没有什么优势。

但是仔细一看会发现，比对是在内存中完成中，不涉及到磁盘IO，耗时可以忽略不计。

另外 B-tree 中一个节点中可以存放很多的关键字（个数由阶决定），相同数量的关键字在 B-tree 中生成的节点要远远少于二叉树中的节点，相差的节点数量就等同于磁盘IO的次数。这样到达一定数量后，性能的差异就显现出来了。

插入

当 B-tree 要进行插入关键字时，都是直接找到叶子节点进行操作。

1. 根据要插入的关键字查找到待插入的叶子节点；
2. 因为一个节点的子节点的最大个数（阶）为 m，所以需要判断当前节点关键字的个数是否小于 (m - 1)。
   • 是：直接插入
   • 否：发生节点分裂，以节点的中间的关键字将该节点分为左右两部分，中间的关键字放到父节点中即可。

操作流程

比如我们现在需要在 Max Degree（阶）为 3 的 B-tree 插入元素：72

1. 查找待插入的叶子节点

   

2. 节点分裂：本来应该和 [70,88] 在同一个磁盘块上，但是当一个节点有 3 个关键字的时候，它就有可能有 4 个子节点，就超过了我们所定义限制的最大度数 3，所以此时必须进行分裂：以中间关键字为界将节点一分为二，产生一个新节点，并把中间关键字上移到父节点中。

Tip : 当中间关键字有两个时，通常将左关键字进行上移分裂。

删除

删除操作就会比查找和插入要麻烦一些，因为要被删除的关键字可能在叶子节点上，也可能不在，而且删除后还可能导致 B-treeSuchen Sie nach dem Suchen nach Schlüsselwörtern einen Knoten, lesen Sie den Knoten in den Speicher und finden Sie dann das Schlüsselwort durch sequentielle oder binäre Suche. Wenn das Schlüsselwort nicht gefunden wird, müssen Sie die Größe beurteilen, um einen geeigneten Zweig zu finden und mit der Suche fortzufahren.

Operationsprozess

Jetzt müssen Sie das Element finden: 88

Erstes Mal: ​​Festplatten-IO🎜🎜🎜 🎜Zweites Mal: ​​Disk IO🎜🎜🎜🎜Das dritte Mal: ​​Disk IO🎜🎜Dann gibt es einen Speichervergleich, der mit 70 bzw. 88 verglichen wird und schließlich 88 findet. 🎜🎜🎜🎜Beim Suchvorgang haben wir festgestellt, dass sich die Anzahl der Vergleiche und die Anzahl der Festplatten-IOs von B-tree tatsächlich nicht wesentlich von denen von Binärbäumen unterscheiden. Es scheint, dass es keinen Vorteil gibt. 🎜🎜Aber wenn Sie genauer hinschauen, werden Sie feststellen, dass der Vergleich im Speicher abgeschlossen wird, keine Festplatten-E/A erfordert und der Zeitverbrauch vernachlässigbar ist. 🎜🎜Darüber hinaus kann ein Knoten im B-tree viele Schlüsselwörter (die Anzahl wird durch die Reihenfolge bestimmt) und die gleiche Anzahl Schlüsselwörter strong> Die im B-tree generierten Knoten sind weitaus kleiner als die Knoten im Binärbaum, und der Unterschied in der Anzahl der Knoten entspricht der Anzahl der Festplatten-E/As. Ab einer bestimmten Zahl macht sich der Leistungsunterschied bemerkbar. 🎜

Einfügen

🎜Wenn B-tree Schlüsselwörter einfügen möchte, findet es direkt den Blattknoten und führt die Operation aus. 🎜🎜🎜Suchen Sie den einzufügenden Blattknoten anhand des einzufügenden Schlüsselworts🎜Da die maximale Anzahl (Reihenfolge) der untergeordneten Knoten eines Knotens m ist, müssen Sie diese bestimmen der aktuelle Knoten Ob die Anzahl der Schlüsselwörter kleiner als (m - 1) ist.

🎜Ja: direktes Einfügen🎜Nein: Es erfolgt eine Knotenaufteilung. Der Knoten wird basierend auf dem mittleren Schlüsselwort des Knotens in einen linken und einen rechten Teil unterteilt und das mittlere Schlüsselwort wird platziert Klicken Sie einfach auf den übergeordneten Knoten.

Operationsprozess

🎜Zum Beispiel müssen wir jetzt B-Baum Element einfügen: 72🎜🎜🎜🎜Finden Sie den einzufügenden Blattknoten🎜🎜🎜🎜🎜Knotenaufteilung: Es hätte in der sein sollen Gleiche Stelle wie [70,88] Auf einem Festplattenblock, aber wenn ein Knoten 3 Schlüsselwörter hat, kann er 4 untergeordnete Knoten haben, was den maximalen Grad 3 des von uns definierten Grenzwerts überschreitet, also muss aufgeteilt werden Zu diesem Zeitpunkt ausführen >: Teilen Sie den Knoten in zwei Teile, indem Sie das mittlere Schlüsselwort als Grenze verwenden, generieren Sie einen neuen Knoten und verschieben Sie das mittlere Schlüsselwort nach oben zum übergeordneten Knoten. 🎜🎜🎜🎜Tipp: Wenn es zwei mittlere Schlüsselwörter gibt, wird das linke Schlüsselwort normalerweise nach oben verschoben. Verschieben und Teilt. 🎜

Löschen

🎜Der Löschvorgang ist problematischer als das Suchen und Einfügen, da sich das zu löschende Schlüsselwort möglicherweise auf dem Blattknoten befindet und nicht Am Ende kann es auch zu einem Ungleichgewicht des B-Baums kommen und Vorgänge wie Zusammenführen und Drehen sind erforderlich, um das Gleichgewicht des gesamten Baums aufrechtzuerhalten. 🎜🎜Nehmen Sie einfach einen Baum (Level 5) als Beispiel 🎜

Das obige ist der detaillierte Inhalt vonVerstehen Sie endlich, dass der MySQL-Index B+tree verwenden muss und dass er so schnell ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!