Heim >häufiges Problem >Was ist die Breitendurchquerung eines Graphen ähnlich einem Binärbaum?
Was ist die Breitendurchquerung eines Graphen ähnlich einem Binärbaum?
- 青灯夜游Original
- 2020-08-29 16:44:3222608Durchsuche
Die Breitendurchquerung eines Diagramms ist eine horizontale Durchquerung, ähnlich der schichtweisen Durchquerung eines Binärbaums. Die Breitendurchquerung durchsucht und durchläuft die Breite des Baums ausgehend vom Wurzelknoten, d. h. jede Schicht wird nacheinander von oben nach unten und in jeder Schicht von links nach rechts (oder rechts) durchlaufen nach links) Um auf Knoten zuzugreifen, gehen Sie nach dem Zugriff auf eine Ebene zur nächsten Ebene über, bis kein Knoten mehr erreichbar ist.

1. Einführung
Ähnlich wie bei der Baumdurchquerung beginnt auch die Diagrammdurchquerung an einem bestimmten Punkt im Diagramm und besucht dann alle Scheitelpunkte im Diagramm gemäß einer bestimmten Methode und besucht sie nur einmal.
Aber das Durchqueren von Graphen ist komplizierter als das Durchqueren von Bäumen. Da jeder Scheitelpunkt im Diagramm an andere Scheitelpunkte angrenzen kann, müssen die besuchten Scheitelpunkte während der Diagrammdurchquerung aufgezeichnet werden, um wiederholte Besuche zu vermeiden.
Je nach unterschiedlichen Suchpfaden können wir die Methoden der Graphendurchquerung in zwei Typen unterteilen: Breitensuche und Tiefensuche.
2. Grundkonzepte von Graphen
2.1. Ungerichtete Graphen und ungerichtete Graphen
Das Scheitelpunktpaar (u, v) ist ungeordnet, das heißt, (u, v) und (v, u) sind die gleiche Kante. Wird normalerweise durch ein Klammerpaar ausgedrückt.
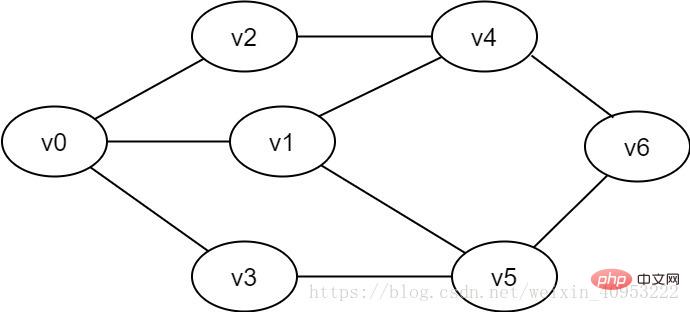
Abbildung 2-1-1 Beispiel eines ungerichteten Graphen
Das Scheitelpunktpaar
2.3. Verbundene Graphen und nicht verbundene Graphen
Unzusammenhängender Graph: Wenn es im ungerichteten Graphen G eine Trennung zwischen v und v' gibt, dann wird G als unzusammenhängender Graph bezeichnet.
Abbildung 2-3 Beispiel eines nicht zusammenhängenden Diagramms
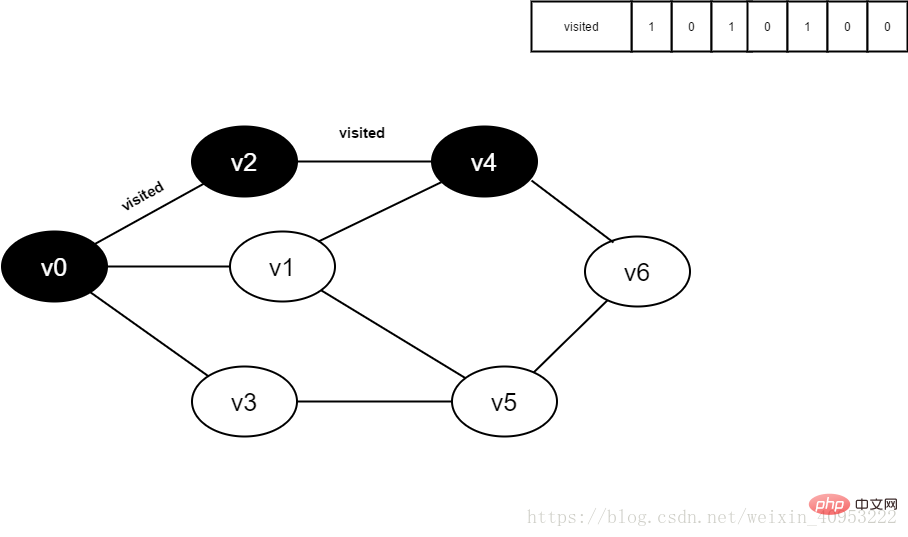
3. Breitensuche3.1. Die Breitensuche ähnelt der hierarchischer Durchlaufprozess eines Baumes. Es muss mithilfe einer Warteschlange implementiert werden. Wie in Abbildung 2-1-1 gezeigt, können wir, wenn wir jeden Scheitelpunkt von v0 bis v6 durchlaufen möchten, v0 als erste Ebene, v1, v2 und v3 als zweite Ebene und v4 und v5 als dritte Ebene festlegen. und v6 Für die vierte Schicht wird jeder Scheitelpunkt jeder Schicht einzeln durchlaufen.
Der spezifische Prozess ist wie folgt:
1. Erstellen Sie ein besuchtes Array, um die besuchten Eckpunkte aufzuzeichnen. Erstellen Sie eine Warteschlange, um die Eckpunkte jeder Ebene zu initialisieren. 
2. Starten Sie den Besuch ab v0 im Bild, setzen Sie den Wert des besuchten Arrays[v0] auf true und fügen Sie v0 zur Warteschlange hinzu.
3. Solange die Warteschlange nicht leer ist, wiederholen Sie die folgenden Vorgänge: (1) Klicken Sie oben im Team auf u, um die Warteschlange zu verlassen.
(2) Überprüfen Sie nacheinander alle benachbarten Scheitelpunkte w von u. Wenn der Wert von „visited[w]“ falsch ist, besuchen Sie w, setzen Sie „visited[w]“ auf „true“ und fügen Sie w zur Warteschlange hinzu. 3.2. Algorithmus-Implementierungsprozess
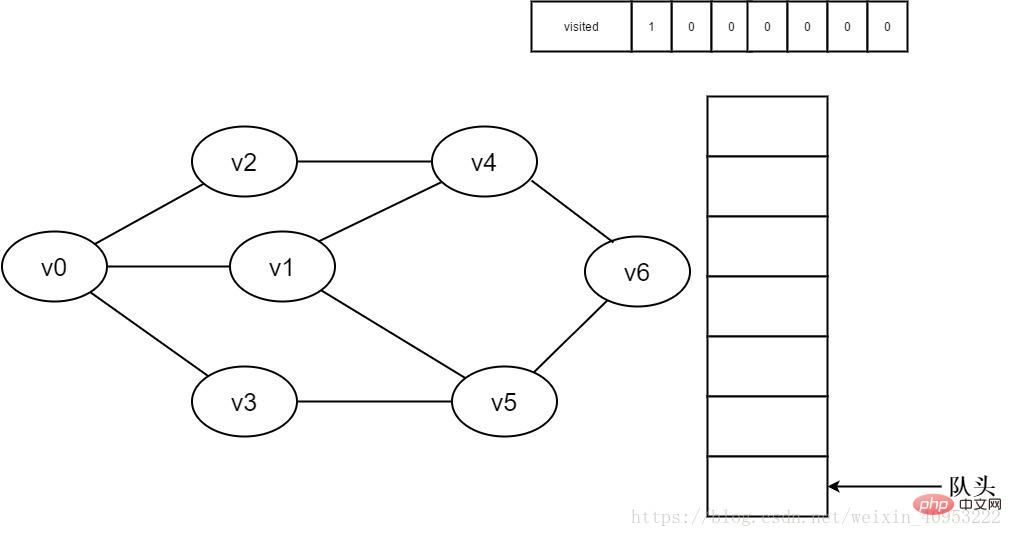
Weiß bedeutet nicht besucht, grau bedeutet bald besucht und schwarz bedeutet besucht. visited-Array: 0 bedeutet nicht besucht, 1 bedeutet besucht. Warteschlange: Elemente kommen am Anfang der Warteschlange heraus und Elemente kommen am Ende hinzu. 1. Zunächst wurden nicht alle Scheitelpunkte besucht, das besuchte Array ist auf 0 initialisiert und es befinden sich keine Elemente in der Warteschlange.
Abbildung 3-2-1
2 wird bald besucht.
Abbildung 3-2-2
 3. Besuchen Sie den Scheitelpunkt v0, setzen Sie den Wert von besuchte[0] auf 1 und fügen Sie v0 zur Warteschlange hinzu.
3. Besuchen Sie den Scheitelpunkt v0, setzen Sie den Wert von besuchte[0] auf 1 und fügen Sie v0 zur Warteschlange hinzu.
Bild 3-2-3
4. Entfernen Sie v0 aus der Warteschlange und besuchen Sie den benachbarten Punkt v2. Bestimmen Sie besucht [2], da der Wert von besucht [2] 0 ist, besuchen Sie v2.
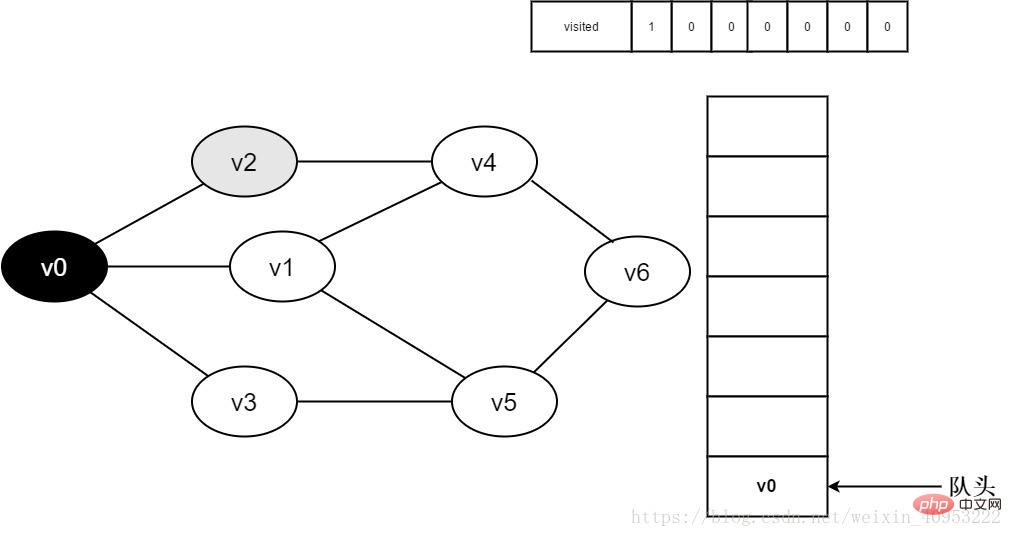
Abbildung 3-2-4
5. Setzen Sie „besucht“[2] auf 1 und fügen Sie v2 zur Warteschlange hinzu.
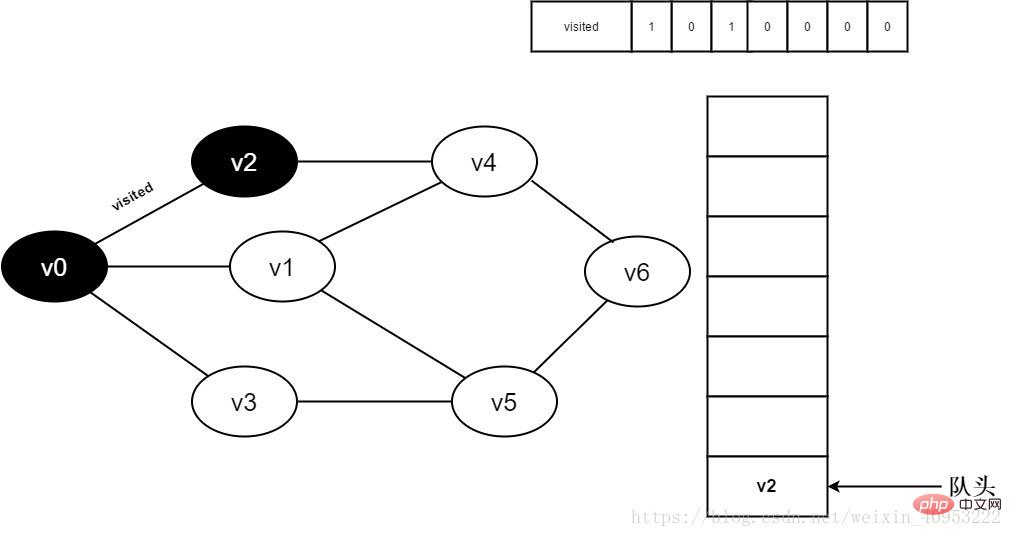
Abbildung 3-2-5
6. Besuchen Sie v0 angrenzenden Punkt v1. Bestimmen Sie besucht[1], da der Wert von besucht[1] 0 ist, besuchen Sie v1.
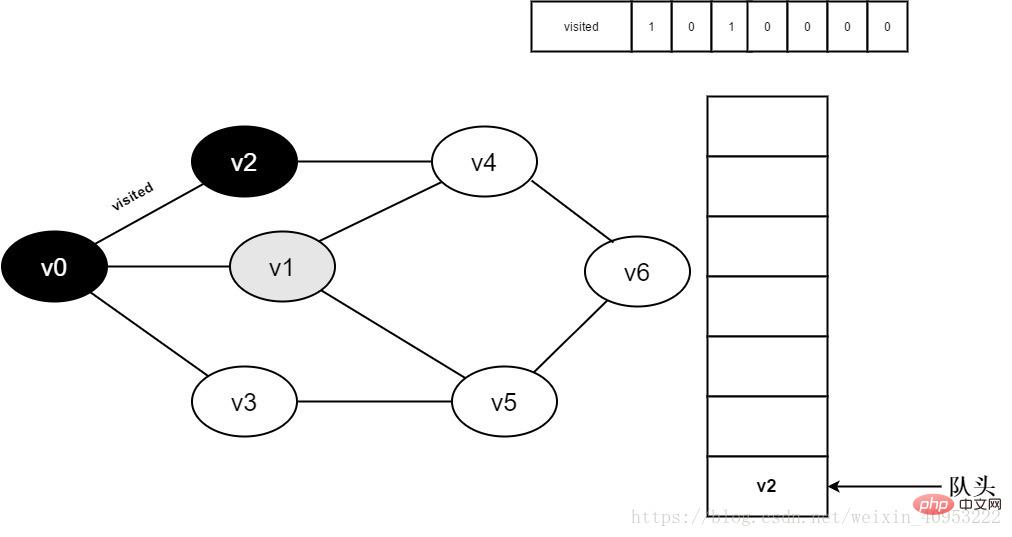
Abbildung 3-2-6
7. Setzen Sie besuchte[1] auf 0 und fügen Sie v1 zur Warteschlange hinzu.
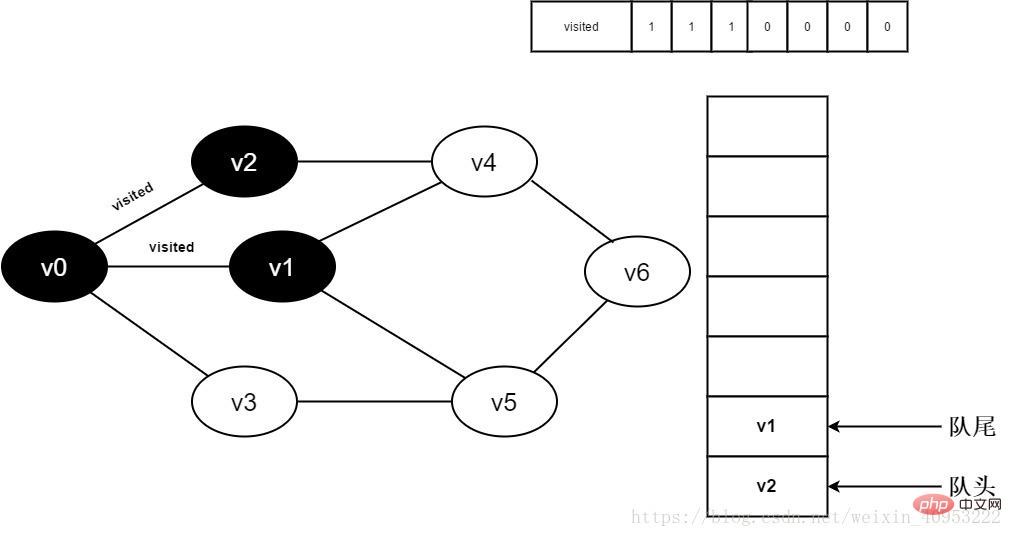
Abbildung 3-2-7
8. Da der Wert 0 ist, besuchen Sie v3. Setzen Sie besuchte[3] auf 0 und stellen Sie v3 in die Warteschlange.
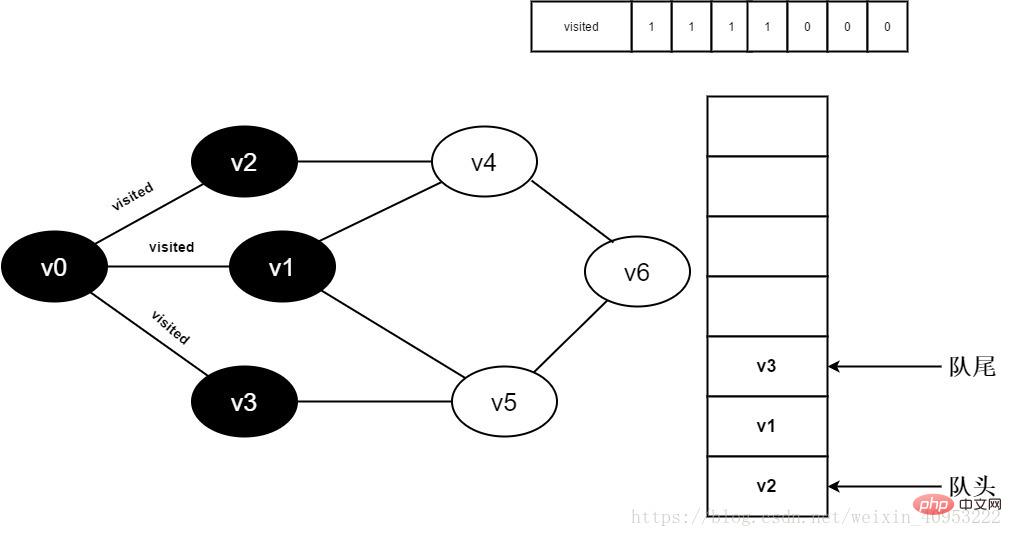
Abbildung 3-2-8
Alle angrenzenden Punkte von 9.v0 wurden besucht. Entfernen Sie das Kopfelement v2 aus der Warteschlange und beginnen Sie mit dem Besuch aller benachbarten Punkte von v2.
Beginnen Sie mit dem Besuch von v2 neben dem Punkt v0 und beurteilen Sie, ob er [0] besucht hat, da sein Wert 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin v2 neben Punkt v4, bestimmen Sie den besuchten Punkt[4], da sein Wert 0 ist, besuchen Sie v4, wie unten gezeigt:
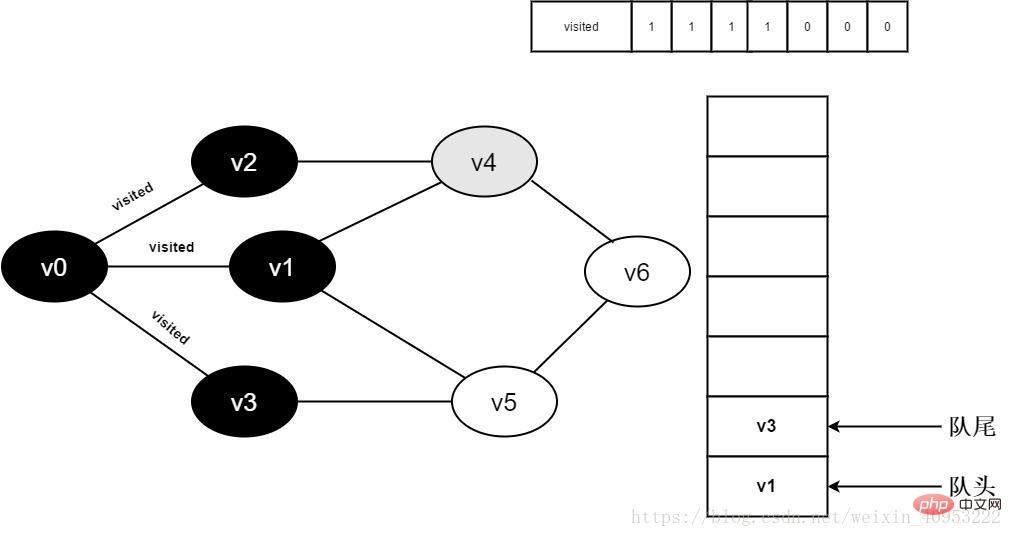
Abbildung 3-2-9
10. 4] Auf 1 setzen und v4 in die Warteschlange stellen.

Abbildung 3-2-10
Alle angrenzenden Punkte von 11.v2 wurden besucht. Entfernen Sie das Kopfelement v1 aus der Warteschlange und beginnen Sie mit dem Besuch aller benachbarten Punkte von v1.
Beginnen Sie mit dem Besuch von v1 neben dem Punkt v0, da der besuchte [0]-Wert 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin v1 neben dem Punkt v4, da der Wert von besuchte[4] 1 ist, wird kein Besuch durchgeführt.
Fahren Sie mit dem Besuch von v1 neben dem Punkt v5 fort, da der besuchte[5]-Wert 0 ist, besuchen Sie v5, wie unten gezeigt:

Abbildung 3-2-11
12 1 und fügen Sie v5 zum Team hinzu.
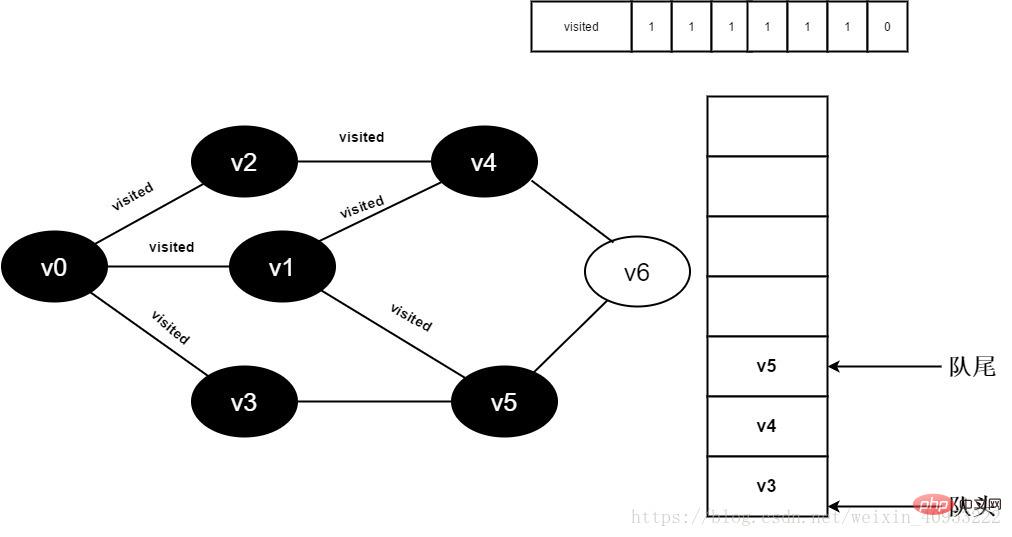
Abbildung 3-2-12 Alle angrenzenden Punkte von
13.v1 wurden besucht. Entfernen Sie das Kopfelement v3 aus der Warteschlange und beginnen Sie mit dem Zugriff auf alle angrenzenden Punkte von v3.
Beginnen Sie mit dem Besuch von v3 neben dem Punkt v0, da der besuchte [0]-Wert 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin den v3-Nachbarpunkt v5, da der besuchte[5]-Wert 1 ist, wird kein Besuch durchgeführt.
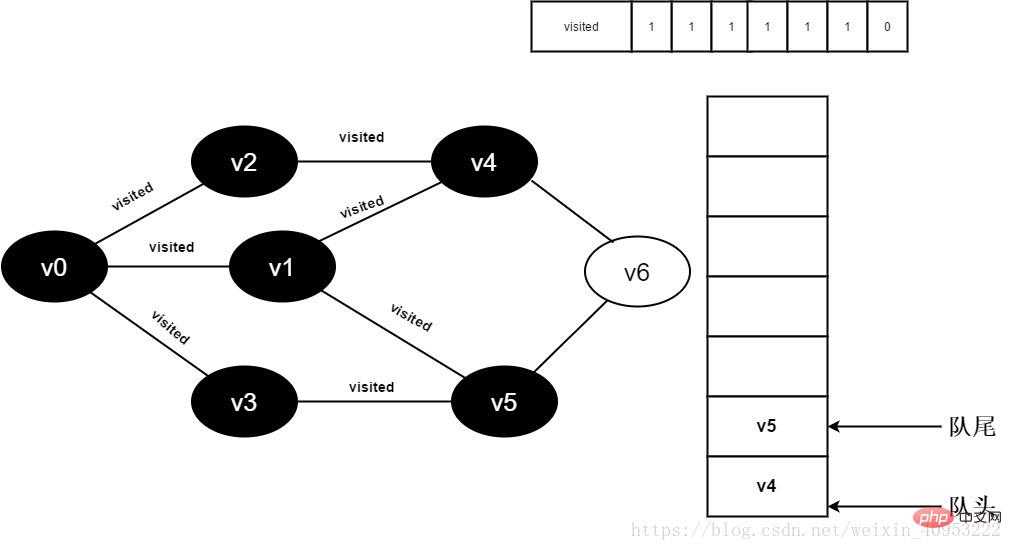
Abbildung 3-2-13 Alle angrenzenden Punkte von
14.v3 wurden aus der Warteschlange entfernt und alle angrenzenden Punkte von v4 werden besucht.
Beginnen Sie mit dem Besuch des benachbarten Punkts v2 von v4. Da der Wert von besuchte[2] 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin den angrenzenden Punkt v6 von v4, da der Wert von besuchte[6] 0 ist, besuchen Sie v6, wie unten gezeigt:
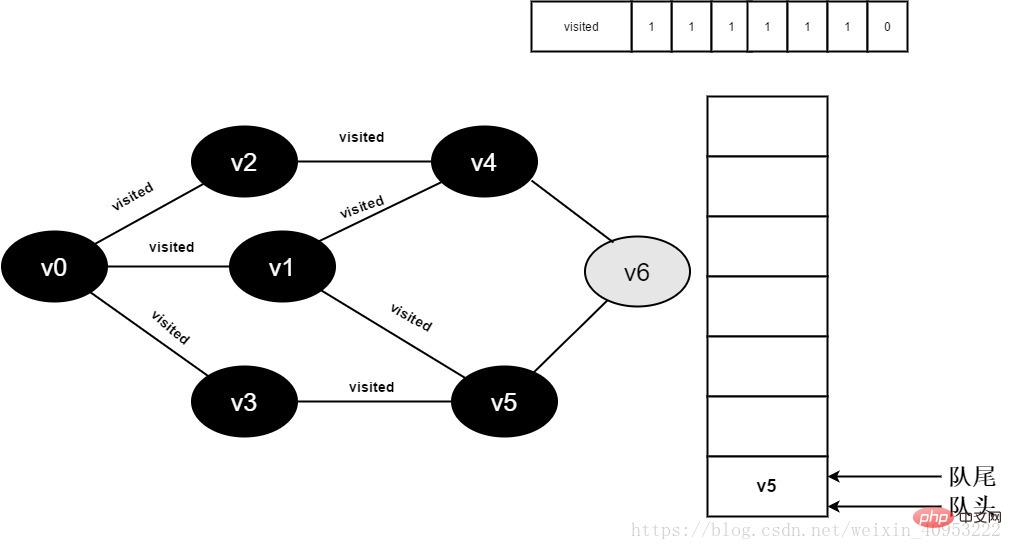
Abbildung 3-2-14
15 Der Wert von „visited[6]“ ist 1 und wird v6 in die Warteschlange gestellt.
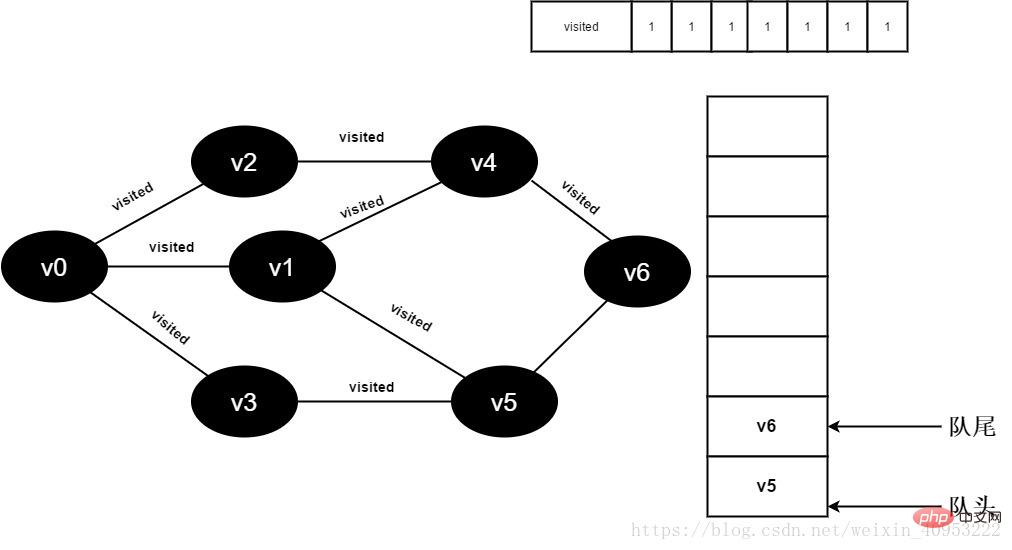
Abbildung 3-2-15 Alle angrenzenden Punkte von
16.v4 wurden aus der Warteschlange entfernt und alle angrenzenden Punkte von v5 werden besucht.
Beginnen Sie mit dem Besuch des v5-Nachbarpunkts v3. Da der Wert von besuchte[3] 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin den Nachbarpunkt v5 v6, da der Wert von besuchte[6] 1 ist, wird kein Besuch durchgeführt.
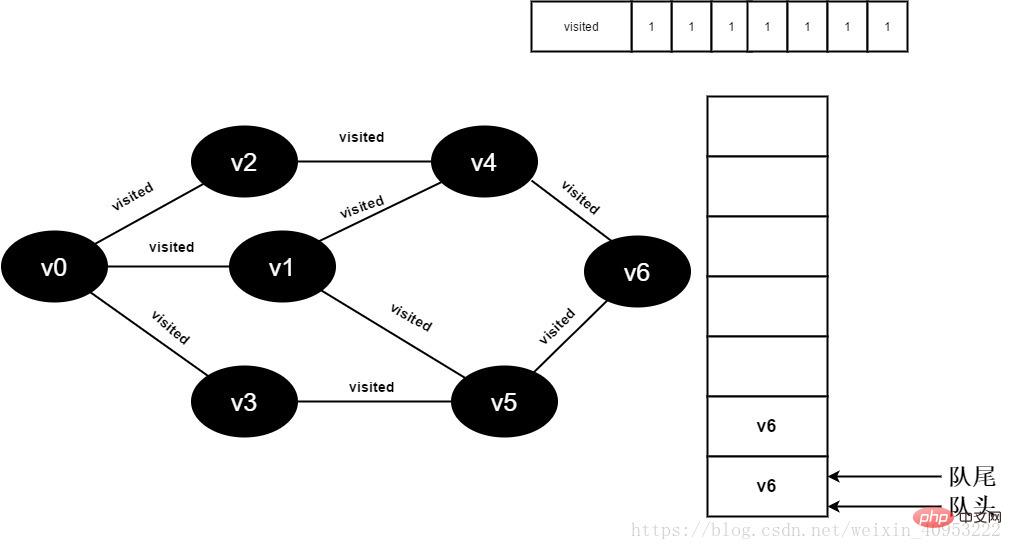
Abbildung 3-2-16
Alle angrenzenden Punkte von 17.v5 wurden besucht. Entfernen Sie das Kopfelement v6 aus der Warteschlange und beginnen Sie mit dem Zugriff auf alle angrenzenden Punkte von v6.
Beginnen Sie mit dem Besuch des v6-Nachbarpunkts v4, da der Wert von besuchte[4] 1 ist, wird kein Besuch durchgeführt.
Besuchen Sie weiterhin den Nachbarpunkt v6 v5, da der Wert von besuchte[5] 1 ist, sodass kein Besuch durchgeführt wird.
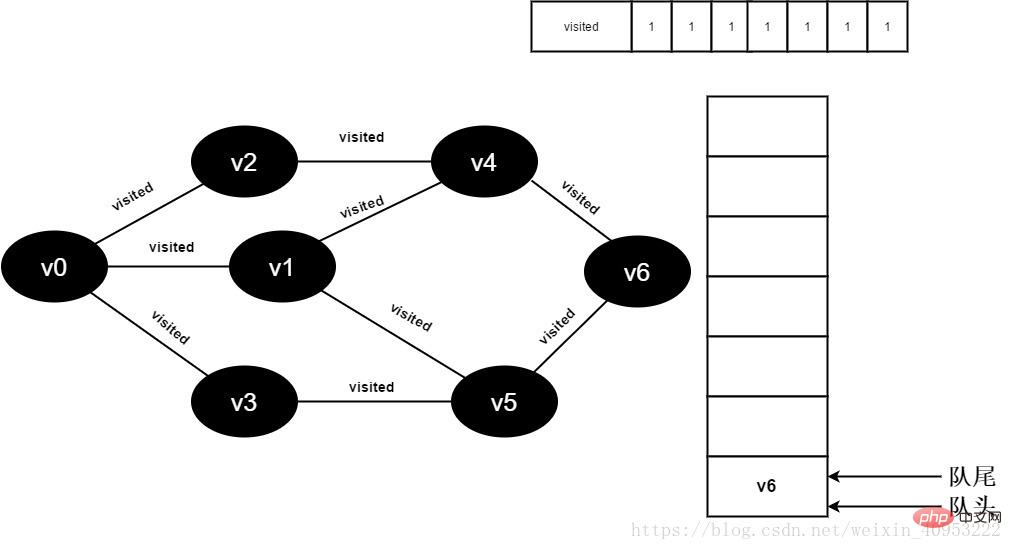
Abbildung 3-2-17
18. Die Warteschlange ist leer, verlassen Sie die Schleife und alle Eckpunkte wurden besucht.

Abbildung 3-2-18
3.3 Implementierung von spezifischem Code
3.3.1 Verwenden Sie die Adjazenzmatrix, um die Breitensuche des Diagramms darzustellen
/*一些量的定义*/ queue<char> q; //定义一个队列,使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;
/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}3.3.2 Repräsentieren ein Diagramm unter Verwendung einer Adjazenzliste. Breitensuche Die Suche ähnelt der Vorbestellungsdurchquerung eines Baums. Der spezifische Prozess ist wie folgt:
Vorbereitung: Erstellen Sie ein besuchtes Array, um alle besuchten Scheitelpunkte aufzuzeichnen.
1. Beginnen Sie bei v0 im Bild und besuchen Sie v0.
2. Finden Sie den ersten nicht besuchten Nachbarpunkt von v0 und besuchen Sie den Scheitelpunkt. Verwenden Sie diesen Scheitelpunkt als neuen Scheitelpunkt und wiederholen Sie diesen Schritt, bis der gerade besuchte Scheitelpunkt keine nicht besuchten benachbarten Scheitelpunkte mehr hat.
3. Kehren Sie zum zuvor besuchten Scheitelpunkt zurück, der noch nicht besuchte benachbarte Punkte hat, und fahren Sie mit dem Besuch des nächsten nicht besuchten Leitpunkts des Scheitelpunkts fort.
4. Wiederholen Sie die Schritte 2 und 3, bis alle Eckpunkte besucht sind und die Suche beendet ist.
4.2 Implementierungsprozess des Algorithmus
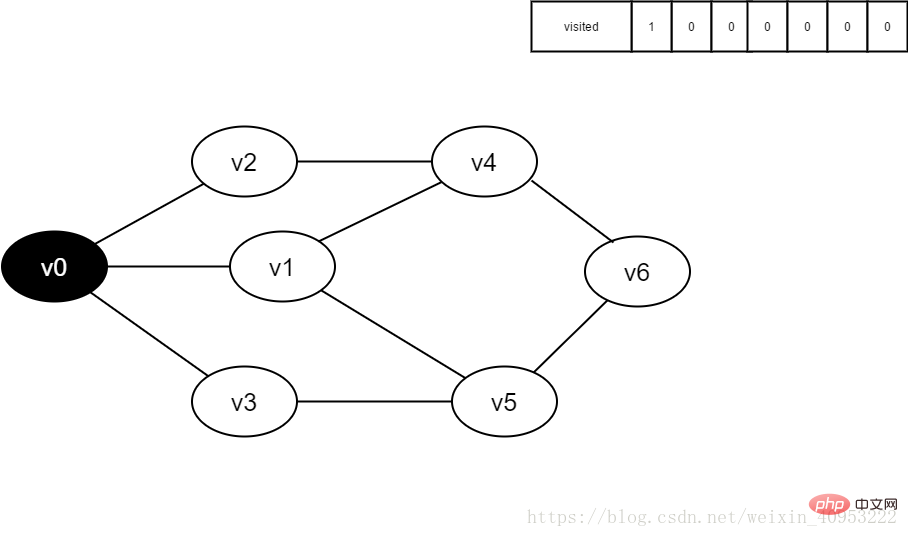
1 Zunächst wurden nicht alle Scheitelpunkte besucht und das besuchte Array ist leer.
Abbildung 4-2-1 2 Kurz vor dem Besuch von v0.
2 Kurz vor dem Besuch von v0.
 3 Besuchen Sie v0 und setzen Sie den Wert von besuchte[0] auf 1.
3 Besuchen Sie v0 und setzen Sie den Wert von besuchte[0] auf 1.
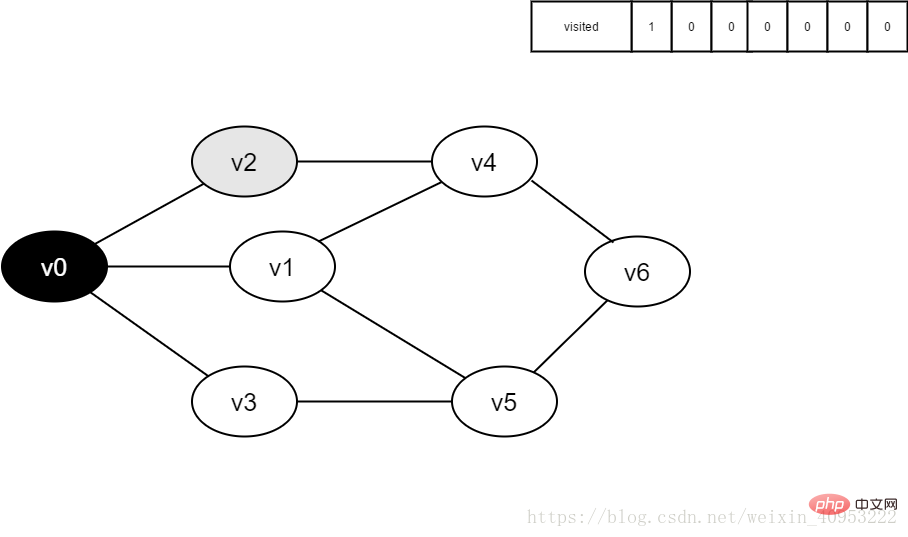
 4. Besuchen Sie den benachbarten Punkt v2 von v0, besuchen Sie den Richter [2], da sein Wert 0 ist, besuchen Sie v2.
4. Besuchen Sie den benachbarten Punkt v2 von v0, besuchen Sie den Richter [2], da sein Wert 0 ist, besuchen Sie v2.
 5 besucht[2] auf 1.
5 besucht[2] auf 1.
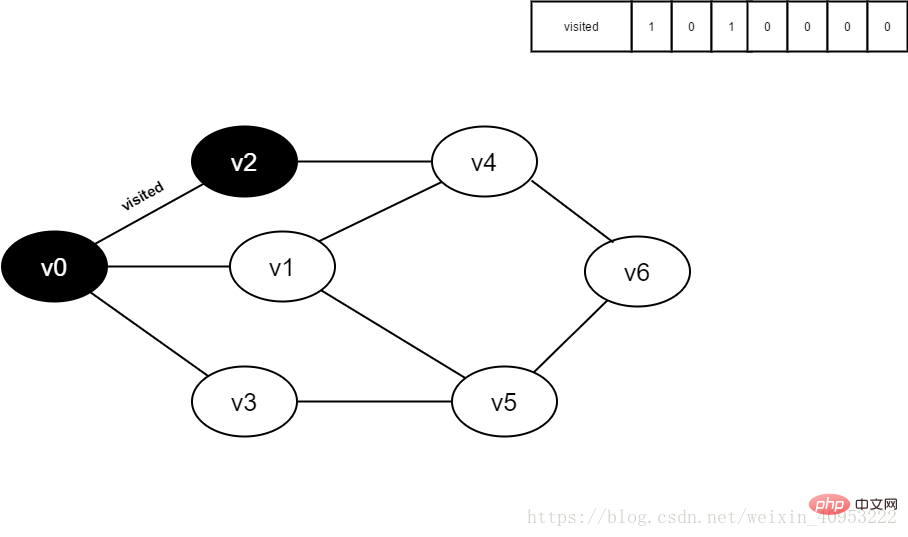 6. Besuchen Sie den benachbarten Punkt v0 von v2, besuchen Sie den Richter [0], sein Wert ist 1, nicht besuchen.
6. Besuchen Sie den benachbarten Punkt v0 von v2, besuchen Sie den Richter [0], sein Wert ist 1, nicht besuchen.
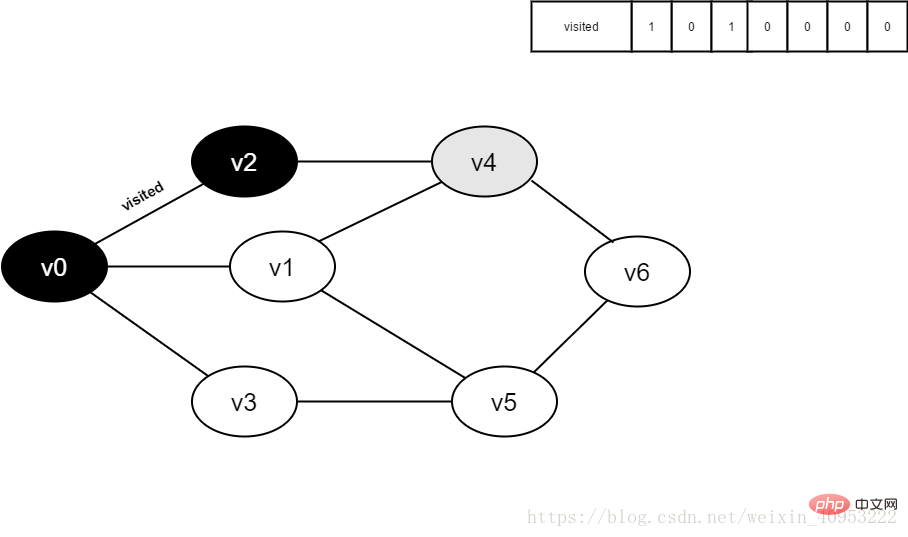 7 Besucht[4] auf 1 setzen.
7 Besucht[4] auf 1 setzen.
Abbildung 4-2-7
Abbildung 4-2-8
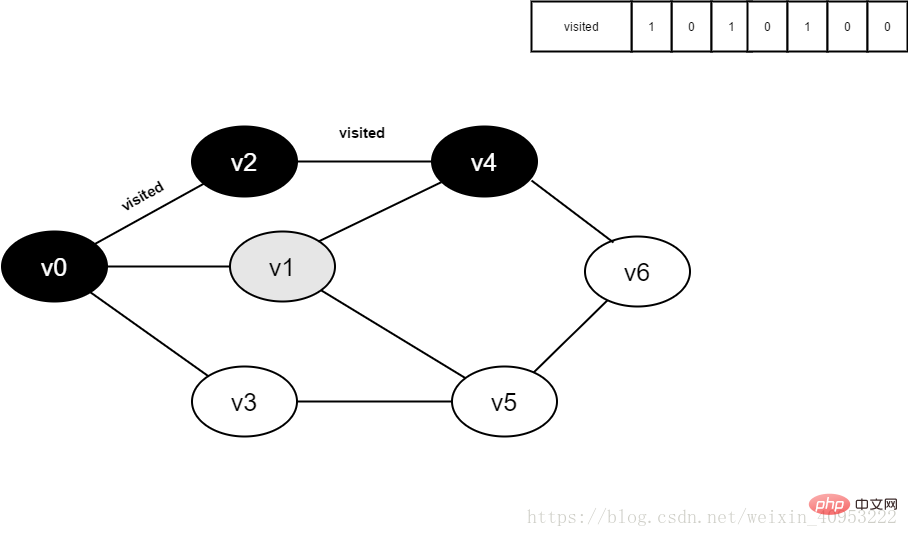 9 Besucht[1] auf 1.
9 Besucht[1] auf 1.
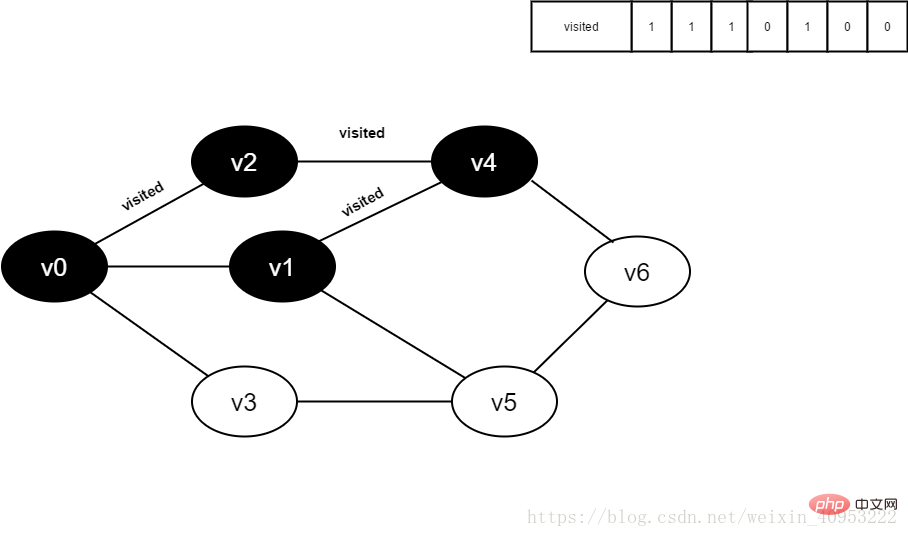 10. Besuchen Sie den benachbarten Punkt v0 von v1, besuchen Sie den Richter [0], sein Wert ist 1, nicht besuchen.
10. Besuchen Sie den benachbarten Punkt v0 von v1, besuchen Sie den Richter [0], sein Wert ist 1, nicht besuchen.
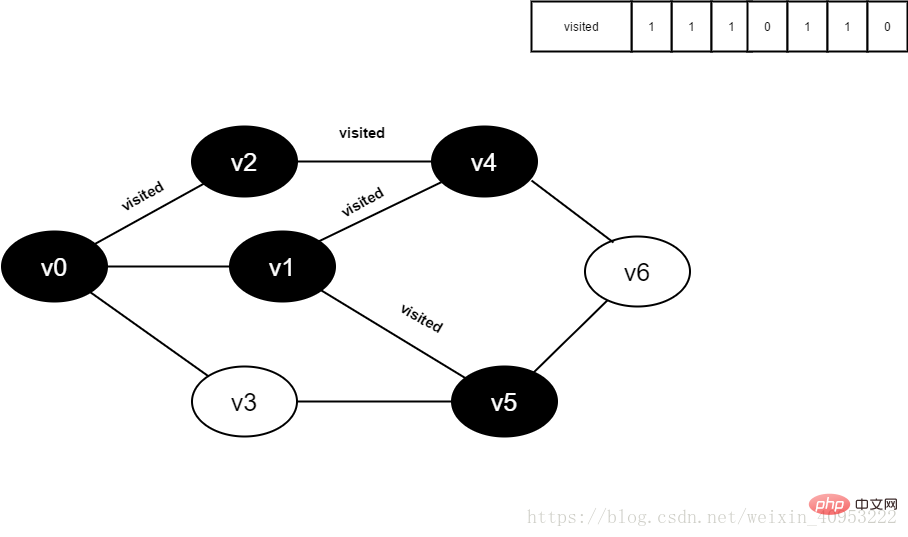
Besuchen Sie weiterhin den benachbarten Punkt v5 von v1, interpretieren Sie den besuchten Punkt [5], sein Wert ist 0, und besuchen Sie v5.
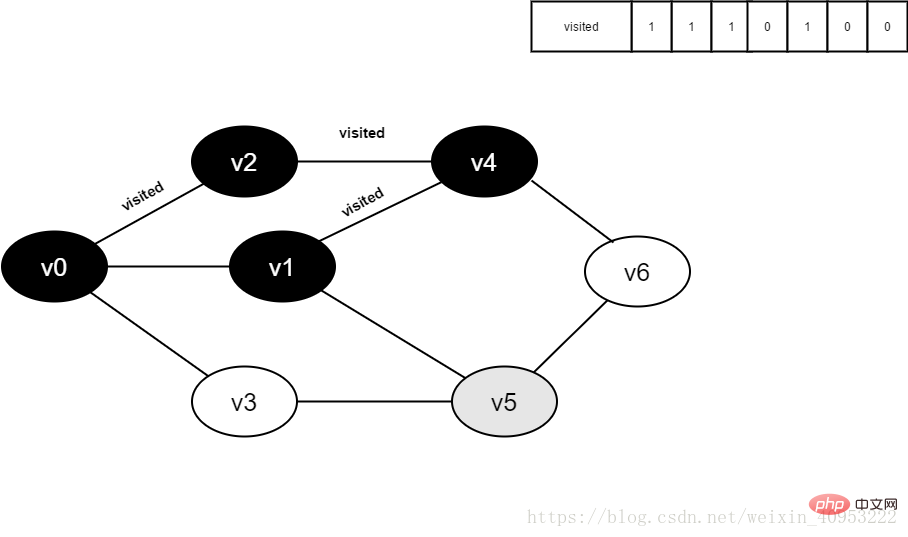 11 besucht[5] auf 1.
11 besucht[5] auf 1.
 12. Besuchen Sie den angrenzenden Punkt v1, Richter besucht[1], sein Wert ist 1, nicht besuchen.
12. Besuchen Sie den angrenzenden Punkt v1, Richter besucht[1], sein Wert ist 1, nicht besuchen.
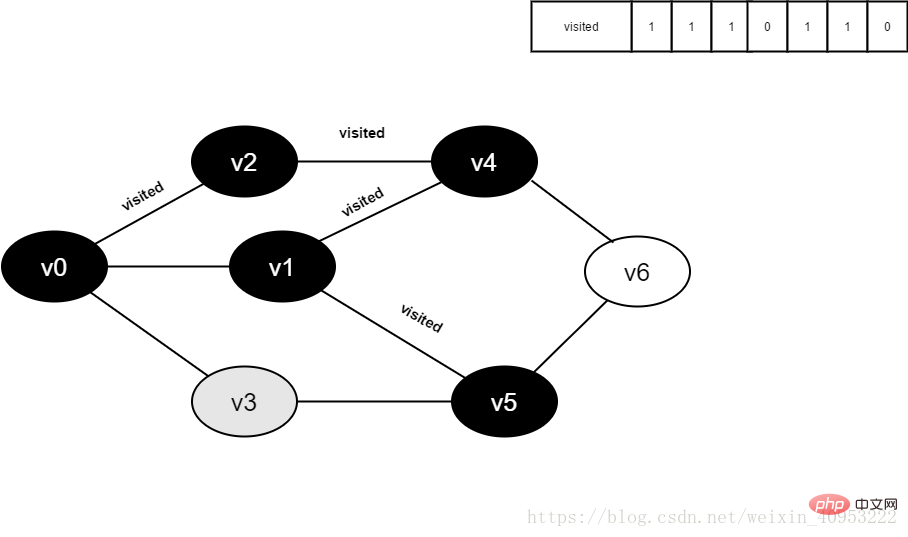
图4-2-12
13.将visited[1]置为1。
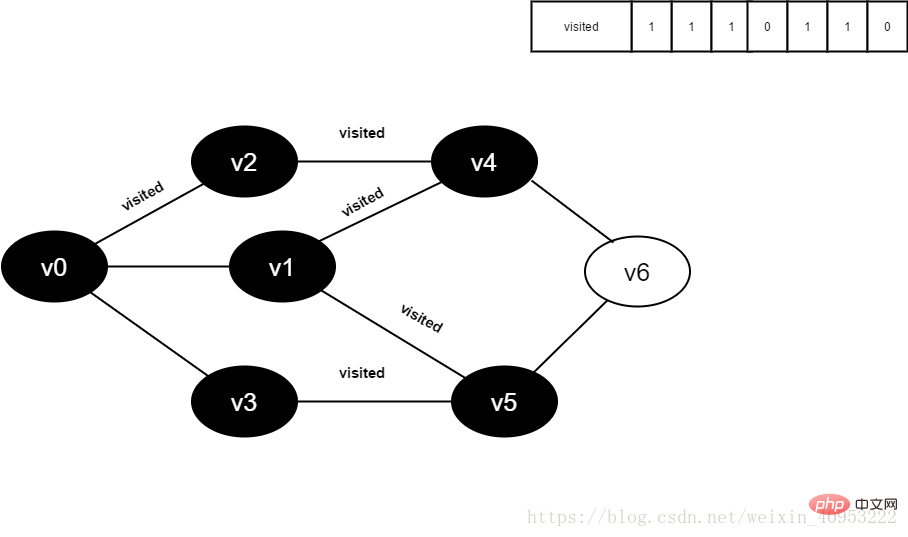
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
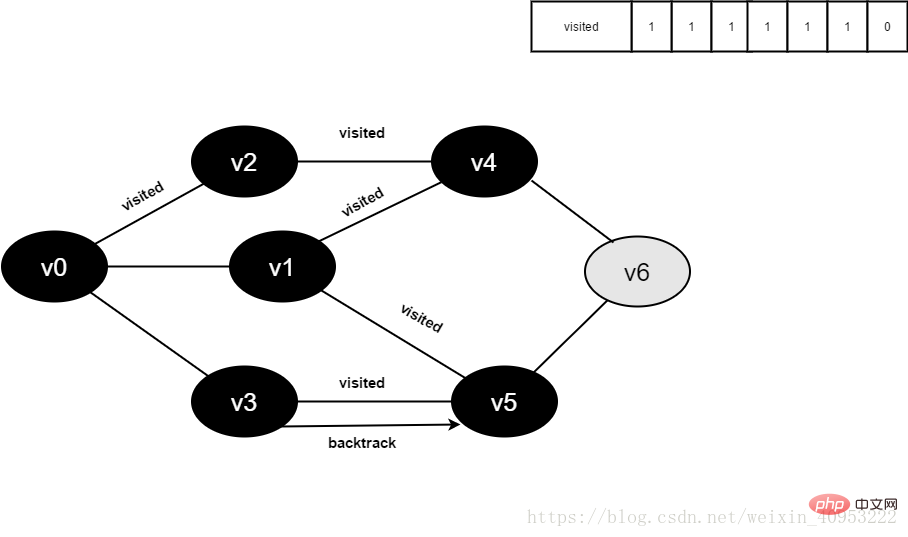
图4-2-14
15.将visited[6]置为1。
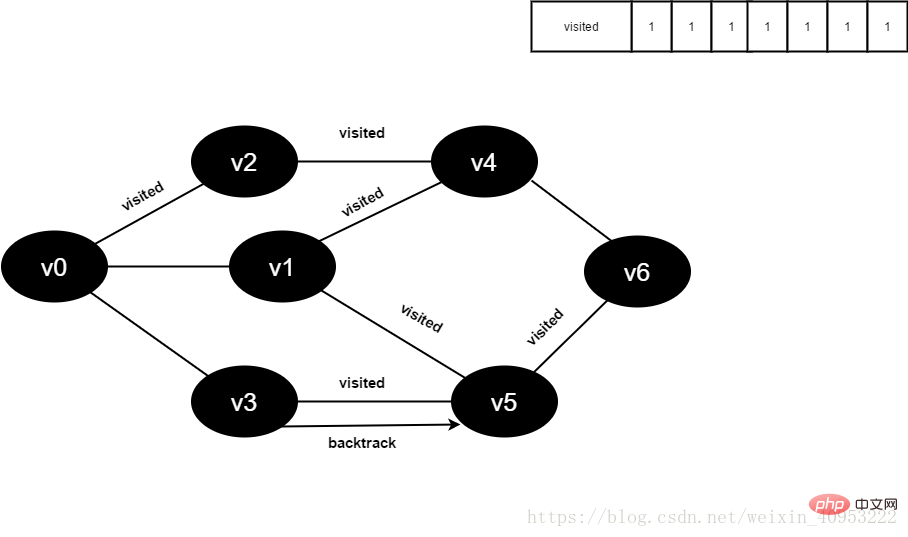
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
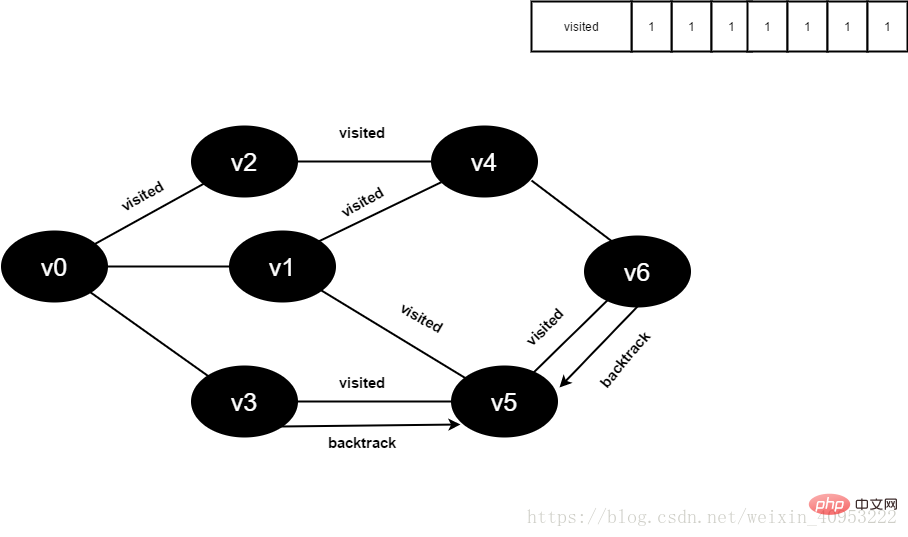
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
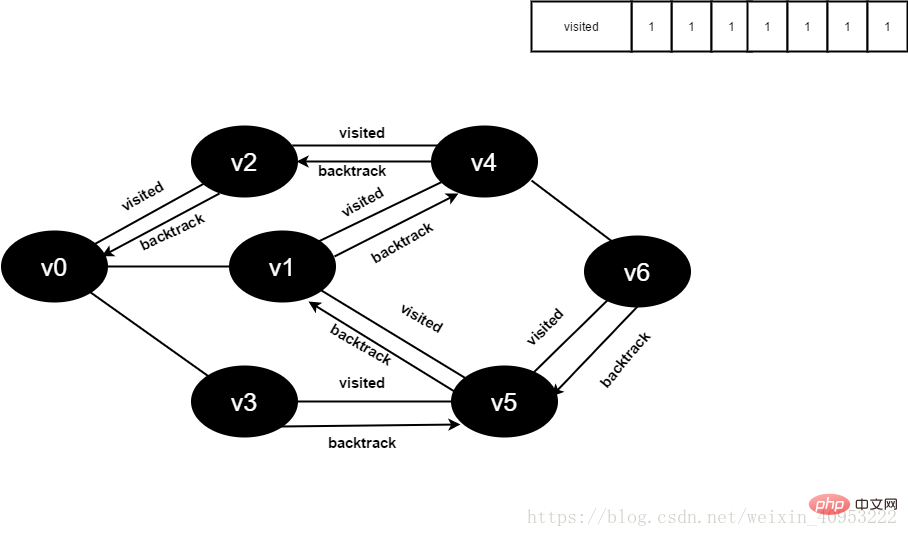
图4-2-17
4.3具体代码实现
4.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}4.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}
更多相关知识,请访问:PHP中文网!
Das obige ist der detaillierte Inhalt vonWas ist die Breitendurchquerung eines Graphen ähnlich einem Binärbaum?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Redis-Methode zum Durchlaufen aller Schlüssel
- Python iteriert über das längste Wort in der Ausgabeliste
- Sollten Sie sich aus Leistungsgründen für die Schleifendurchquerung entscheiden?
- Es gibt mehrere Möglichkeiten, Objekte in JS zu durchlaufen
- Detaillierte Erläuterung der Tiefendurchquerung von Binärbäumen in Java
- Wie durchlaufe ich alle Elemente einer Liste in Python?