Detaillierte Erläuterung der Tiefendurchquerung von Binärbäumen in Java

In den letzten zwei Tagen habe ich Algorithmusfragen im Zusammenhang mit Binärbäumen bearbeitet und einige Studiennotizen gemacht. (Sie wissen nicht einmal, wie man Binärbäume erstellt? Sie sind wirklich nicht kompetent und müssen in Ihrer täglichen Arbeit keine Algorithmen oder Datenstrukturen schreiben, die sich auf Binärbäume beziehen. Weil ich gut darin bin, muss ich es tun lerne härter!)

Definition

Erster Blick auf die Erklärung von Wikipedia: In der Informatik ist ein Binärbaum (englisch : Binärbaum) ist ein Baum mit höchstens zwei Zweigen pro Knoten (das heißt, es gibt keine Baumstruktur mit einem Knoten mit einem Zweiggrad größer als 2). Normalerweise werden Zweige als „linker Teilbaum“ oder „rechter Teilbaum“ bezeichnet. Die Zweige eines Binärbaums haben eine linke und eine rechte Reihenfolge und können nicht beliebig umgekehrt werden.

Aufgrund der durch den Binärbaum selbst definierten Eigenschaften weist er ein hohes Maß an lokaler Wiederholbarkeit auf. Daher wird er beim Durchlaufen eines Binärbaums normalerweise auf rekursive Weise implementiert Auf diese Weise ist es sehr prägnant und schön und leichter zu verstehen.

Depth-First-Traversal

Im Allgemeinen haben wir drei gängigste Ordnungsdurchquerungen für die Tiefen-First-Traversation von Binärbäumen: Vorbestellung, Zwischenbestellung und Nachbestellung.

Die Durchlaufreihenfolge der Vorbestellung lautet: Besuchen Sie den Wurzelknoten –> Linker Teilbaum-> Den rechten Teilbaum durchqueren

Die Reihenfolge der Durchquerung lautet: Den linken Teilbaum durchqueren-> >

Hinweis: Links und rechts sind hier der gesamte Teilbaum und kein Knoten, da wir den gesamten Baum durchlaufen müssen, sodass jede Durchquerung in dieser Reihenfolge bis zum Blattknoten durchgeführt wird.

Zum Beispiel, wenn es den folgenden Binärbaum gibt:

Die durch Vorbestellungsdurchquerung erhaltene Sequenz ist A - B - C - D - E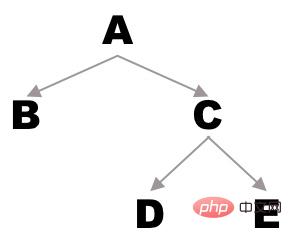

Die durch die Durchquerung mittlerer Ordnung erhaltene Sequenz ist B - A - D - C - E

Die durch Durchquerung nach der Ordnung erhaltene Sequenz ist B - D - E - C - A

Lassen Sie uns diese Idee in Bezug auf die Durchquerung der Vorbestellung verwenden (es wird dringend davon abgeraten, eine menschliche Rekursion zu verwenden, zumindest kann mein Gehirn drei Ebenen nicht ertragen ...):

Rekursion der ersten Ebene:

Besuchen Sie zuerst den Wurzelknoten, geben Sie also Wurzelknoten A aus, durchqueren Sie dann den linken Teilbaum (L1) und durchqueren Sie dann den rechten Teilbaum (R1);

Rekursion der zweiten Ebene:

Besuchen Sie für L1 zuerst den Wurzelknoten. Geben Sie also zu diesem Zeitpunkt den Wurzelknoten B aus, stellen Sie dann fest, dass der linke und rechte Teilbaum von B leer sind, und beenden Sie die Rekursion.

Besuchen Sie für R1 die Wurzel Knoten zuerst, also zu diesem Zeitpunkt den Wurzelknoten C ausgeben und dann den linken Teilbaum (L2) und dann den rechten Teilbaum (R2) durchlaufen

Rekursion der dritten Ebene:

Für L2, der Wurzelknoten wird zuerst besucht, daher wird zu diesem Zeitpunkt der Wurzelknoten D ausgegeben. Stellen Sie dann fest, dass der linke und rechte Teilbaum von D leer sind, und beenden Sie die Rekursion.

Besuchen Sie für R2 die Wurzel Knoten zuerst, also geben Sie zu diesem Zeitpunkt den Wurzelknoten E aus und stellen Sie dann fest, dass der linke und rechte Teilbaum von E leer sind. Beenden Sie die Rekursion

Merkmale der vorderen, mittleren und hinteren Ordnung

Nach der Definition von vorderer, mittlerer und hinterer Ordnung fällt es uns tatsächlich nicht schwer, die folgenden Merkmale zu finden:

• Das erste in der Vor- Reihenfolge muss der Wurzelknoten sein, und der letzte in der Nachfolge muss der Wurzelknoten sein

• Die Verteilung des linken Teilbaums und des rechten Teilbaums für jede Sortierung ist regelmäßig

• Für alle Unterbaum folgt den beiden oben genannten Regeln, der Baum

Diese Merkmale sind auch der Ausdruck der Reihenfolge in der Definition.

Verschiedene Ableitungen

Hier sind einige der grundlegendsten Algorithmusfragen für die Binärbaumdurchquerung:

• Gegeben ist eine Binärdatei Baum, erhalte die Reihenfolge seiner Vor-/Mittel-/Nachordnungsdurchquerung;

• Ableitung der Nachordnung (oder Ableitung des gesamten Binärbaums) basierend auf der Vor- und Mittelordnung

• Basierend auf der Nachbestellung und um die Vorbestellung abzuleiten (oder den gesamten Binärbaum abzuleiten);

Für die Binärbaumdurchquerung wird, wie bereits erwähnt, normalerweise eine Rekursion verwendet. Für die Rekursion gibt es eine Vorlage, die direkt angewendet werden kann:

public void recur(int level, int param) {
    
    // terminator
    if (level > MAX_LEVEL) {
        // process result
         return;   
    }
    
    // process current logic
    process(level, param);
    
    // drill down
    recur(level+1, newParam);
    
    // restore current status
}

Dies ist ein praktischerer Tipp, den Bruder Chao (Qin Chao) im Algorithmus-Trainingslager erwähnt hat, das ich in den letzten zwei Tagen gesehen habe (diese Vorlage ist besonders gut für Anfänger). Befolgen Sie die drei oben genannten Schritte (wenn lokale Variablen benötigt werden, erfolgt die Freigabe oder zusätzliche Verarbeitung in Schritt 4). Sie können rekursiven Code auf geordnetere Weise schreiben.

Hier ist ein Beispiel für die Ableitung einer Nachbestellung basierend auf einer Vorbestellung und einer Zwischenbestellung:

Initialisieren Sie zunächst die beiden Sequenzen:

int[] preSequence = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] inSequence = {2, 3, 1, 6, 7, 8, 5, 9, 4};

Durch die verschiedenen oben genannten Funktionen , wir haben Das minimale wiederholte Unterproblem kann gefunden werden Jede Rekursion

stimmt mit dem Index i des Knotenwerts in der Reihenfolge überein, der dem ersten Knotenwert

der vorherigen Sequenz entspricht Wir können den vorderen und hinteren Teil des Index i abrufen, der dem linken bzw. rechten Teilbaum entspricht, und dann die beiden linken bzw. rechten Teilbäume durchlaufen und dann den ersten Knotenwert der aktuellen Vorbestellung ausgeben, der der Wurzelknoten ist.

Gemäß der Top-Down-Programmiermethode können wir zunächst den folgenden ersten rekursiven Aufruf schreiben:

List<Integer> result = new ArrayList<>();
preAndInToPost(0, 0, preSequence.length, preSequence, inSequence, result);

Der erste Parameter stellt den ersten Elementindex der Vorbestellungssequenz dar; >Der zweite Parameter stellt den ersten Elementindex der In-Order-Sequenz dar;

Der dritte Parameter stellt die Länge der Sequenz dar;

第四个参数表示前序序列；

第五个参数表示后序序列；

第六个参数用于保存结果；

先来考虑终止条件是什么，也就是什么时候结束递归，当我们的根结点为空的时候终止，对应这里就是序列长度为零的时候。

if (length == 0) {
    return;
}

接着考虑处理逻辑，也就是找到索引 i：

int i = 0;
while (inSequence[inIndex + i] != preSequence[preIndex]) {
    i++;
}

然后开始向下递归：

preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
result.add(preSequence[preIndex]);

因为推导的是后序序列，所以顺序如上，添加根结点的操作是在最后的。前三个参数如何得出来的呢，我们走一下第一次遍历就可以得出来。

前序序列的第一个结点 1 在中序序列中的索引为 2，此时

左子树的中序系列起始索引为总序列的第 1 个索引，长度为 2；

左子树的前序序列起始索引为总序列的第 2 个索引，长度为 2；

右子树的中序系列起始索引为总序列的第 3 个索引，长度为 length - 3；

右子树的前序序列起始索引为总序列的第 3 个索引，长度为 length - 3；

完整代码如下：

/**
 * 根据前序和中序推导后序
 *
 * @param preIndex    前序索引
 * @param inIndex     中序索引
 * @param length      序列长度
 * @param preSequence 前序序列
 * @param inSequence  中序序列
 * @param result      结果序列
 */
private void preAndInToPost(int preIndex, int inIndex, int length, int[] preSequence, int[] inSequence, List<Integer> result) {
    if (length == 0) {
        return;
    }

    int i = 0;
    while (inSequence[inIndex + i] != preSequence[preIndex]) {
        i++;
    }

    preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
    preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
    result.add(preSequence[preIndex]);
}

参考链接

• 维基百科 - 二叉树（https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91）

推荐教程：《java教程》

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Tiefendurchquerung von Binärbäumen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!