Ein Artikel, um zu verstehen, wie man einen binären Suchbaum in JS implementiert

Eine der am häufigsten verwendeten und diskutierten Datenstrukturen in der Informatik ist der binäre Suchbaum. Dies ist normalerweise die erste Datenstruktur, die mit einem nichtlinearen Einfügungsalgorithmus eingeführt wird. Binäre Suchbäume ähneln doppelt verknüpften Listen. Jeder Knoten enthält einige Daten und zwei Zeiger auf andere Knoten. Sie unterscheiden sich in der Art und Weise, wie diese Knoten miteinander verknüpft sind. Die Zeiger auf binäre Suchbaumknoten werden oft als „links“ und „rechts“ bezeichnet und werden verwendet, um den Teilbaum anzugeben, der dem aktuellen Wert zugeordnet ist. Eine einfache JavaScript-Implementierung eines solchen Knotens lautet wie folgt:

var node = {
    value: 125,
    left: null,
    right: null
};

Wie Sie am Namen erkennen können, ist ein binärer Suchbaum in einer hierarchischen baumähnlichen Struktur organisiert. Das erste Element wird zum Wurzelknoten und jeder zusätzliche Wert wird dem Baum als Vorfahre dieser Wurzel hinzugefügt. Allerdings sind die Werte auf den Knoten eines binären Suchbaums eindeutig und nach dem Wert geordnet, den sie enthalten: Da die Werte im linken Teilbaum eines Knotens immer kleiner sind als der Wert des Knotens, sind die Werte in Der rechte Teilbaum ist immer größer als der Wert des Knotens. Auf diese Weise wird das Auffinden von Werten in einem binären Suchbaum sehr einfach. Solange der gesuchte Wert kleiner als der Knoten ist, an dem Sie arbeiten, gehen Sie nach links. Wenn der Wert größer ist, gehen Sie nach rechts. In einem binären Suchbaum dürfen keine Duplikate vorhanden sein, da durch Duplikate die Beziehung unterbrochen wird. Die folgende Abbildung stellt einen einfachen binären Suchbaum dar.

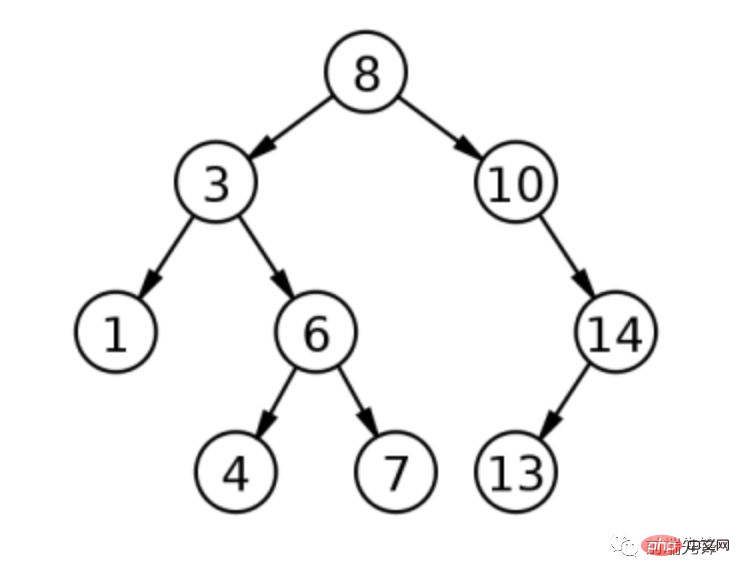
Die obige Abbildung stellt einen binären Suchbaum mit einem Wurzelwert von 8 dar. Wenn der Wert 3 hinzugefügt wird, wird er zum linken untergeordneten Element der Wurzel, da 3 kleiner als 8 ist. Wenn der Wert 1 hinzugefügt wird, wird er zum linken Kind von 3, da 1 kleiner als 8 ist (also links) und 1 dann kleiner als 3 ist (wieder links). Wenn der Wert 10 hinzugefügt wird, wird er zum rechten untergeordneten Element von follow, da 10 größer als 8 ist. Setzen Sie diesen Vorgang mit den Werten 6, 4, 7, 14 und 13 fort. Die Tiefe dieses binären Suchbaums beträgt 3, was bedeutet, dass der Knoten, der am weitesten von der Wurzel entfernt ist, drei Knoten hat.

Binäre Suchbäume werden in einer natürlich sortierten Reihenfolge angezeigt, sodass sie zum schnellen Auffinden von Daten verwendet werden können, da Sie Möglichkeiten für jeden Schritt sofort ausschließen können. Suchen können schneller durchgeführt werden, indem die Anzahl der zu findenden Knoten begrenzt wird. Angenommen, Sie möchten den Wert 6 im Baum oben finden. Beginnend bei der Wurzel stellen wir fest, dass 6 kleiner als 8 ist, also gehen wir zum linken Kind der Wurzel. Da 6 größer als 3 ist, gelangen Sie zum rechten Knoten. Sie können den richtigen Wert finden. Sie müssen also nur drei statt neun Knoten besuchen, um diesen Wert zu finden.

Um einen binären Suchbaum in JavaScript zu implementieren, besteht der erste Schritt darin, eine Basisschnittstelle zu definieren:

function BinarySearchTree() {
    this._root = null;
}

BinarySearchTree.prototype = {

    //restore constructor
    constructor: BinarySearchTree,

    add: function (value){
    },

    contains: function(value){
    },

    remove: function(value){
    },

    size: function(){
    },

    toArray: function(){
    },

    toString: function(){
    }

};

Die Basisschnittstelle ähnelt anderen Datenstrukturen, mit Methoden zum Hinzufügen und Löschen von Werten. Ich habe auch einige praktische Methoden hinzugefügt, size(), toArray() und toString(), die für JavaScript nützlich sind.

Um die Verwendung binärer Suchbäume zu beherrschen, beginnen Sie am besten mit der Methode contains(). Die contains()-Methode akzeptiert einen Wert als Argument und gibt true zurück, wenn der Wert im Baum vorhanden ist, andernfalls gibt sie false zurück. Diese Methode folgt einem einfachen binären Suchalgorithmus, um festzustellen, ob der Wert vorhanden ist:

BinarySearchTree.prototype = {

    //more code

    contains: function(value){
        var found       = false,
            current     = this._root

        //make sure there's a node to search
        while(!found && current){

            //if the value is less than the current node's, go left
            if (value < current.value){
                current = current.left;

            //if the value is greater than the current node&#39;s, go right
            } else if (value > current.value){
                current = current.right;

            //values are equal, found it!
            } else {
                found = true;
            }
        }

        //only proceed if the node was found
        return found;
    },

    //more code

};

Die Suche beginnt an der Wurzel des Baums. Wenn keine Daten hinzugefügt werden, ist möglicherweise kein Root vorhanden. Sie müssen dies überprüfen. Das Durchlaufen des Baums folgt dem einfachen Algorithmus, der zuvor besprochen wurde: Bewegen Sie sich nach links, wenn der gesuchte Wert kleiner als der aktuelle Knoten ist, und bewegen Sie sich nach rechts, wenn der Wert größer ist. Der current-Zeiger wird jedes Mal überschrieben, bis der gesuchte Wert gefunden wird (in diesem Fall wird found auf true gesetzt) ​​oder in dieser Richtung keine Knoten mehr vorhanden sind (in diesem Fall ist der Wert nicht aktiviert). Bäume).

Die in contains() verwendeten Methoden können auch zum Einfügen neuer Werte in den Baum verwendet werden. Der Hauptunterschied besteht darin, dass Sie nach der Stelle suchen, an der der neue Wert eingefügt werden soll, und nicht nach dem Wert im Baum:

BinarySearchTree.prototype = {

    //more code

    add: function(value){
        //create a new item object, place data in
        var node = {
                value: value,
                left: null,
                right: null
            },

            //used to traverse the structure
            current;

        //special case: no items in the tree yet
        if (this._root === null){
            this._root = node;
        } else {
            current = this._root;

            while(true){

                //if the new value is less than this node's value, go left
                if (value < current.value){

                    //if there&#39;s no left, then the new node belongs there
                    if (current.left === null){
                        current.left = node;
                        break;
                    } else {
                        current = current.left;
                    }

                //if the new value is greater than this node&#39;s value, go right
                } else if (value > current.value){

                    //if there&#39;s no right, then the new node belongs there
                    if (current.right === null){
                        current.right = node;
                        break;
                    } else {
                        current = current.right;
                    }       

                //if the new value is equal to the current one, just ignore
                } else {
                    break;
                }
            }
        }
    },

    //more code

};

Der Sonderfall beim Hinzufügen eines Werts in einem binären Suchbaum ist, wenn kein Wert vorhanden ist Wurzel. In diesem Fall reicht es aus, den Stamm einfach auf einen neuen Wert zu setzen. In anderen Fällen ist der grundlegende Algorithmus genau derselbe wie in contains(): Gehen Sie nach links, wenn der neue Wert kleiner als der aktuelle Knoten ist, und nach rechts, wenn der Wert größer ist. Der Hauptunterschied besteht darin, dass hier der neue Wert angezeigt wird, wenn Sie nicht weiter gehen können. Wenn Sie also nach links gehen müssen, aber kein linker Knoten vorhanden ist, ist der neue Wert der linke Knoten (derselbe wie der rechte Knoten). Da es keine Duplikate gibt, stoppt der Vorgang, wenn ein Knoten mit demselben Wert gefunden wird.

在继续讨论 size() 方法之前，我想深入讨论树遍历。为了计算二叉搜索树的大小，必须要访问树中的每个节点。二叉搜索树通常会有不同类型的遍历方法，最常用的是有序遍历。通过处理左子树，然后是节点本身，然后是右子树，在每个节点上执行有序遍历。由于二叉搜索树以这种方式排序，从左到右，结果是节点以正确的排序顺序处理。对于 size() 方法，节点遍历的顺序实际上并不重要，但它对 toArray() 方法很重要。由于两种方法都需要执行遍历，我决定添加一个可以通用的 traverse() 方法：

BinarySearchTree.prototype = {

    //more code

    traverse: function(process){

        //helper function
        function inOrder(node){
            if (node){

                //traverse the left subtree
                if (node.left !== null){
                    inOrder(node.left);
                }            

                //call the process method on this node
                process.call(this, node);

                //traverse the right subtree
                if (node.right !== null){
                    inOrder(node.right);
                }
            }
        }

        //start with the root
        inOrder(this._root);
    },

    //more code

};

此方法接受一个参数 process，这是一个应该在树中的每个节点上运行的函数。该方法定义了一个名为 inOrder() 的辅助函数用于递归遍历树。注意，如果当前节点存在，则递归仅左右移动（以避免多次处理 null ）。然后 traverse() 方法从根节点开始按顺序遍历，process() 函数处理每个节点。然后可以使用此方法实现size()、toArray()、toString()：

BinarySearchTree.prototype = {

    //more code

    size: function(){
        var length = 0;

        this.traverse(function(node){
            length++;
        });

        return length;
    },

    toArray: function(){
        var result = [];

        this.traverse(function(node){
            result.push(node.value);
        });

        return result;
    },

    toString: function(){
        return this.toArray().toString();
    },

    //more code

};

size() 和 toArray() 都调用 traverse() 方法并传入一个函数来在每个节点上运行。在使用 size()的情况下，函数只是递增长度变量，而 toArray() 使用函数将节点的值添加到数组中。 toString()方法在调用 toArray() 之前把返回的数组转换为字符串，并返回  。

删除节点时，你需要确定它是否为根节点。根节点的处理方式与其他节点类似，但明显的例外是根节点需要在结尾处设置为不同的值。为简单起见，这将被视为 JavaScript 代码中的一个特例。

删除节点的第一步是确定节点是否存在：

BinarySearchTree.prototype = {

    //more code here

    remove: function(value){

        var found       = false,
            parent      = null,
            current     = this._root,
            childCount,
            replacement,
            replacementParent;

        //make sure there's a node to search
        while(!found && current){

            //if the value is less than the current node's, go left
            if (value < current.value){
                parent = current;
                current = current.left;

            //if the value is greater than the current node&#39;s, go right
            } else if (value > current.value){
                parent = current;
                current = current.right;

            //values are equal, found it!
            } else {
                found = true;
            }
        }

        //only proceed if the node was found
        if (found){
            //continue
        }

    },
    //more code here

};

remove()方法的第一部分是用二叉搜索定位要被删除的节点，如果值小于当前节点的话则向左移动，如果值大于当前节点则向右移动。当遍历时还会跟踪 parent 节点，因为你最终需要从其父节点中删除该节点。当 found 等于 true 时，current 的值是要删除的节点。

删除节点时需要注意三个条件：

1、叶子节点

2、只有一个孩子的节点

3、有两个孩子的节点

从二叉搜索树中删除除了叶节点之外的内容意味着必须移动值来对树正确的排序。前两个实现起来相对简单，只删除了一个叶子节点，删除了一个带有一个子节点的节点并用其子节点替换。最后一种情况有点复杂，以便稍后访问。

在了解如何删除节点之前，你需要知道节点上究竟存在多少个子节点。一旦知道了，你必须确定节点是否为根节点，留下一个相当简单的决策树：

BinarySearchTree.prototype = {

    //more code here

    remove: function(value){

        var found       = false,
            parent      = null,
            current     = this._root,
            childCount,
            replacement,
            replacementParent;

        //find the node (removed for space)

        //only proceed if the node was found
        if (found){

            //figure out how many children
            childCount = (current.left !== null ? 1 : 0) + 
                         (current.right !== null ? 1 : 0);

            //special case: the value is at the root
            if (current === this._root){
                switch(childCount){

                    //no children, just erase the root
                    case 0:
                        this._root = null;
                        break;

                    //one child, use one as the root
                    case 1:
                        this._root = (current.right === null ? 
                                      current.left : current.right);
                        break;

                    //two children, little work to do
                    case 2:

                        //TODO

                    //no default

                }        

            //non-root values
            } else {

                switch (childCount){

                    //no children, just remove it from the parent
                    case 0:
                        //if the current value is less than its 
                        //parent's, null out the left pointer
                        if (current.value < parent.value){
                            parent.left = null;

                        //if the current value is greater than its
                        //parent&#39;s, null out the right pointer
                        } else {
                            parent.right = null;
                        }
                        break;

                    //one child, just reassign to parent
                    case 1:
                        //if the current value is less than its 
                        //parent&#39;s, reset the left pointer
                        if (current.value < parent.value){
                            parent.left = (current.left === null ? 
                                           current.right : current.left);

                        //if the current value is greater than its 
                        //parent&#39;s, reset the right pointer
                        } else {
                            parent.right = (current.left === null ? 
                                            current.right : current.left);
                        }
                        break;    

                    //two children, a bit more complicated
                    case 2:

                        //TODO          

                    //no default

                }

            }

        }

    },

    //more code here

};

处理根节点时，这是一个覆盖它的简单过程。对于非根节点，必须根据要删除的节点的值设置 parent 上的相应指针：如果删除的值小于父节点，则 left 指针必须重置为 null （对于没有子节点的节点）或删除节点的 left 指针；如果删除的值大于父级，则必须将 right 指针重置为 null 或删除的节点的 right指针。

如前所述，删除具有两个子节点的节点是最复杂的操作。考虑二元搜索树的以下表示。

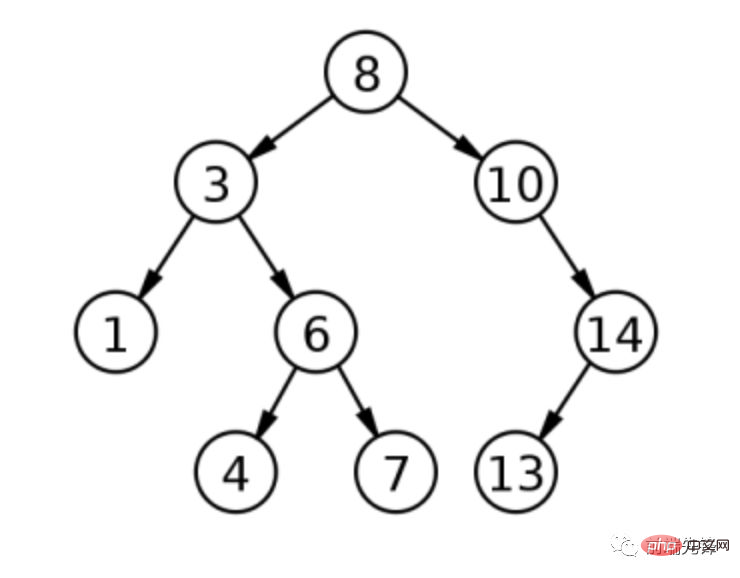
根为 8，左子为 3，如果 3 被删除会发生什么？有两种可能性：1（3 左边的孩子，称为有序前身）或4（右子树的最左边的孩子，称为有序继承者）都可以取代 3。

这两个选项中的任何一个都是合适的。要查找有序前驱，即删除值之前的值，请检查要删除的节点的左子树，并选择最右侧的子节点；找到有序后继，在删除值后立即出现的值，反转进程并检查最左侧的右子树。其中每个都需要另一次遍历树来完成操作：

BinarySearchTree.prototype = {

    //more code here

    remove: function(value){

        var found       = false,
            parent      = null,
            current     = this._root,
            childCount,
            replacement,
            replacementParent;

        //find the node (removed for space)

        //only proceed if the node was found
        if (found){

            //figure out how many children
            childCount = (current.left !== null ? 1 : 0) + 
                         (current.right !== null ? 1 : 0);

            //special case: the value is at the root
            if (current === this._root){
                switch(childCount){

                    //other cases removed to save space

                    //two children, little work to do
                    case 2:

                        //new root will be the old root's left child
                        //...maybe
                        replacement = this._root.left;

                        //find the right-most leaf node to be 
                        //the real new root
                        while (replacement.right !== null){
                            replacementParent = replacement;
                            replacement = replacement.right;
                        }

                        //it's not the first node on the left
                        if (replacementParent !== null){

                            //remove the new root from it's 
                            //previous position
                            replacementParent.right = replacement.left;

                            //give the new root all of the old 
                            //root's children
                            replacement.right = this._root.right;
                            replacement.left = this._root.left;
                        } else {

                            //just assign the children
                            replacement.right = this._root.right;
                        }

                        //officially assign new root
                        this._root = replacement;

                    //no default

                }        

            //non-root values
            } else {

                switch (childCount){

                    //other cases removed to save space 

                    //two children, a bit more complicated
                    case 2:

                        //reset pointers for new traversal
                        replacement = current.left;
                        replacementParent = current;

                        //find the right-most node
                        while(replacement.right !== null){
                            replacementParent = replacement;
                            replacement = replacement.right;
                        }

                        replacementParent.right = replacement.left;

                        //assign children to the replacement
                        replacement.right = current.right;
                        replacement.left = current.left;

                        //place the replacement in the right spot
                        if (current.value < parent.value){
                            parent.left = replacement;
                        } else {
                            parent.right = replacement;
                        }          

                    //no default

                }

            }

        }

    },

    //more code here

};

具有两个子节点的根节点和非根节点的代码几乎相同。此实现始终通过查看左子树并查找最右侧子节点来查找有序前驱。遍历是使用 while 循环中的 replacement 和 replacementParent 变量完成的。

  replacement中的节点最终成为替换 current 的节点，因此通过将其父级的 right 指针设置为替换的 left 指针，将其从当前位置移除。

Wenn replacement für den Wurzelknoten ein direktes untergeordnetes Element des Wurzelknotens ist, wird replacementParent zu null, sodass der replacement-Zeiger von right einfach auf den right-Zeiger von root gesetzt wird.

Der letzte Schritt besteht darin, den Ersatzknoten dem richtigen Standort zuzuweisen. Bei Wurzelknoten wird die Ersetzung auf die neue Wurzel gesetzt; bei Nicht-Wurzelknoten wird die Ersetzung der entsprechenden Position auf dem Original parent zugewiesen.

Ein Hinweis zu dieser Implementierung: Das ständige Ersetzen von Knoten durch geordnete Vorgänger kann zu einem unausgeglichenen Baum führen, in dem sich die meisten Werte auf einer Seite des Baums befinden. Ein unausgeglichener Baum bedeutet eine weniger effiziente Suche und sollte daher in realen Szenarien Anlass zur Sorge geben. Bei der Implementierung eines binären Suchbaums ist es wichtig zu bestimmen, ob ein geordneter Vorgänger oder ein geordneter Nachfolger verwendet werden soll, um den Baum ordnungsgemäß ausbalanciert zu halten (oft als selbstausgleichender binärer Suchbaum bezeichnet).

Der vollständige Quellcode für diese Implementierung des binären Suchbaums finden Sie in meinem GitHub. Für eine alternative Implementierung können Sie sich auch Isaac Schlueters GitHub-Fork ansehen.

Dieser Artikel ist reproduziert von: https://segmentfault.com/a/1190000020044659

Englische Originaladresse: https://humanwhocodes.com/blog/2009/06/ 09/ computer-science-in-javascript-binary-search-tree-part-1/

Autor: Nicholas C. Zakas

Empfohlenes Tutorial: "JavaScript Video Tutorial》

Das obige ist der detaillierte Inhalt vonEin Artikel, um zu verstehen, wie man einen binären Suchbaum in JS implementiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!