Heim >Backend-Entwicklung >C#.Net-Tutorial >Implementierung eines minimalen Spannbaums in der Sprache C
Implementierung eines minimalen Spannbaums in der Sprache C
- angryTomnach vorne
- 2019-11-29 15:24:043803Durchsuche

1. Einführung in den Minimum Spanning Tree
Was ist der Minimum Spanning Tree?
Minimum Spanning Tree (MST) besteht darin, einen Baum T in einem gegebenen ungerichteten Graphen G(V,E) zu finden, sodass dieser Baum alle Scheitelpunkte im Graphen G hat und alle Kanten von den Kanten stammen im Diagramm G und erfüllen die minimale Kantengewichtssumme des gesamten Baums.
2.prim-Algorithmus
ist dem Dijkstra-Algorithmus sehr ähnlich! ! Schauen Sie sich bitte das folgende Gif-Diagramm an. Die Kernidee des Prim-Algorithmus besteht darin, eine Menge S für den Graphen G (V, E) festzulegen, die besuchten Scheitelpunkte zu speichern und dann den Scheitelpunkt mit dem kleinsten kürzesten Abstand von auszuwählen Setze S jedes Mal aus der Menge V-S (bezeichnet als u), greife auf die Menge S zu und verbinde sie. Lassen Sie dann den Scheitelpunkt u den Mittelpunkt sein und optimieren Sie den kürzesten Abstand zwischen allen Scheitelpunkten v, der von u und der Menge s aus erreicht werden kann. Diese Operation wird n-mal ausgeführt, bis die Menge s alle Eckpunkte enthält.
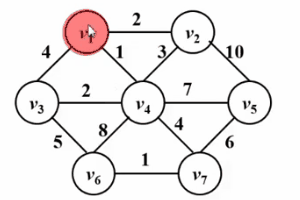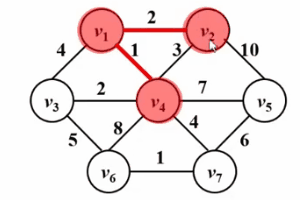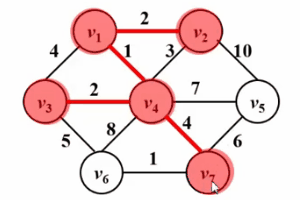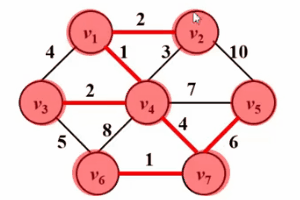
Der Unterschied besteht darin, dass dist im Dijkstra-Algorithmus der kürzeste Weg vom Quellpunkt s zum Scheitelpunkt w ist, während dist im Prim-Algorithmus der kürzeste Weg von der Menge S zum Scheitelpunkt w ist Im Folgenden finden Sie einen Vergleich ihrer Pseudocode-Beschreibungen. Eine detaillierte Beschreibung des Dijkstra-Algorithmus finden Sie im Artikel

Algorithmusimplementierung:
#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 并查集
int dist[MaxVertex]; // 距离
int Nv; // 结点
int Ne; // 边
int sum; // 权重和
using namespace std;
vector<Vertex> MST; // 最小生成树
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv>>Ne;
for(int i=1;i<=Nv;i++){
for(int j=1;j<=Nv;j++)
G[i][j] = 0; // 初始化图
dist[i] = INF; // 初始化距离
parent[i] = -1; // 初始化并查集
}
// 初始化点
for(int i=0;i<Ne;i++){
cin>>v1>>v2>>w;
G[v1][v2] = w;
G[v2][v1] = w;
}
}
// Prim算法前的初始化
void IniPrim(Vertex s){
dist[s] = 0;
MST.push_back(s);
for(Vertex i =1;i<=Nv;i++)
if(G[s][i]){
dist[i] = G[s][i];
parent[i] = s;
}
}
// 查找未收录中dist最小的点
Vertex FindMin(){
int min = INF;
Vertex xb = -1;
for(Vertex i=1;i<=Nv;i++)
if(dist[i] && dist[i] < min){
min = dist[i];
xb = i;
}
return xb;
}
void output(){
cout<<"被收录顺序:"<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<MST[i]<<" ";
cout<<"权重和为:"<<sum<<endl;
cout<<"该生成树为:"<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<parent[i]<<" ";
}
void Prim(Vertex s){
IniPrim(s);
while(1){
Vertex v = FindMin();
if(v == -1)
break;
sum += dist[v];
dist[v] = 0;
MST.push_back(v);
for(Vertex w=1;w<=Nv;w++)
if(G[v][w] && dist[w])
if(G[v][w] < dist[w]){
dist[w] = G[v][w];
parent[w] = v;
}
}
}
int main(){
build();
Prim(1);
output();
return 0;
}Über den Prim-Algorithmus Eine ausführlichere Erklärung finden Sie im Video https://www.bilibili.com/video/av55114968?p=99
3.kruskal-Algorithmus
Kruskal-Algorithmus kann auch verwendet werden Um das Problem des minimalen Spannbaums zu lösen, ist die Idee des Algorithmus leicht zu verstehen:
● Alle Kanten im Diagramm ausblenden im Anfangszustand, sodass jeder Scheitelpunkt im Diagramm ein separater verbundener Block ist und es insgesamt n verbundene Blöcke gibt
● Alle Kanten nach Kantengewicht von klein nach groß sortieren
● Testen Sie alle Kanten entsprechend der Kantengewichtung von klein bis groß. Wenn sich die beiden durch die aktuelle Testkante verbundenen Scheitelpunkte nicht im selben verbundenen Block befinden, wird die Testkante zum aktuellen minimalen Spannbaum hinzugefügt, andernfalls die Kante wird verworfen.
● Wiederholen Sie den vorherigen Schritt, bis die Anzahl der Kanten im minimalen Spannbaum gleich der Gesamtzahl der Scheitelpunkte minus eins ist oder er endet, wenn alle Kanten getestet wurden Der minimale Spannbaum ist kleiner als die Gesamtzahl der Scheitelpunkte minus eins 1, was darauf hinweist, dass der Graph nicht verbunden ist.
Bitte sehen Sie sich das GIF unten an!
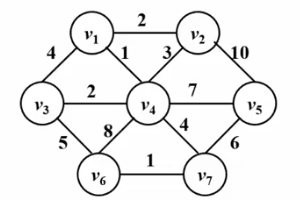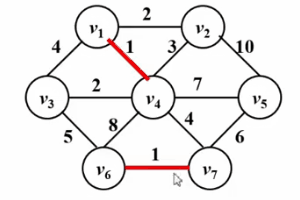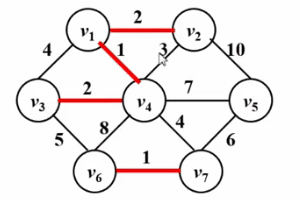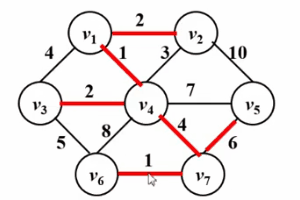
Algorithmusimplementierung:
#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 并查集最小生成树
int Nv; // 结点
int Ne; // 边
int sum; // 权重和
using namespace std;
struct Node{
Vertex v1;
Vertex v2;
int weight; // 权重
// 重载运算符成最大堆
bool operator < (const Node &a) const
{
return weight>a.weight;
}
};
vector<Node> MST; // 最小生成树
priority_queue<Node> q; // 最小堆
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv>>Ne;
for(int i=1;i<=Nv;i++){
for(int j=1;j<=Nv;j++)
G[i][j] = 0; // 初始化图
parent[i] = -1;
}
// 初始化点
for(int i=0;i<Ne;i++){
cin>>v1>>v2>>w;
struct Node tmpE;
tmpE.v1 = v1;
tmpE.v2 = v2;
tmpE.weight = w;
q.push(tmpE);
}
}
// 路径压缩查找
int Find(int x){
if(parent[x] < 0)
return x;
else
return parent[x] = Find(parent[x]);
}
// 按秩归并
void Union(int x1,int x2){
if(parent[x1] < parent[x2]){
parent[x1] += parent[x2];
parent[x2] = x1;
}else{
parent[x2] += parent[x1];
parent[x1] = x2;
}
}
void Kruskal(){
// 最小生成树的边不到 Nv-1 条且还有边
while(MST.size()!= Nv-1 && !q.empty()){
Node E = q.top(); // 从最小堆取出一条权重最小的边
q.pop(); // 出队这条边
if(Find(E.v1) != Find(E.v2)){ // 检测两条边是否在同一集合
sum += E.weight;
Union(E.v1,E.v2); // 并起来
MST.push_back(E);
}
}
}
void output(){
cout<<"被收录顺序:"<<endl;
for(Vertex i=0;i<Nv;i++)
cout<<MST[i].weight<<" ";
cout<<"权重和为:"<<sum<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<parent[i]<<" ";
cout<<endl;
}
int main(){
build();
Kruskal();
output();
return 0;
}Eine detailliertere Erklärung des Kruskal-Algorithmus finden Sie im Video https://www.bilibili.com/ video/av55114968?p =100
Empfohlener Kurs: C Language Tutorial
Das obige ist der detaillierte Inhalt vonImplementierung eines minimalen Spannbaums in der Sprache C. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

