Ausführliche Erläuterung von Beispielen für minimal aufspannende Bäume

Minimaler Spannbaum – Prim-Algorithmus und Kruskal-Algorithmus

Der Spannbaum eines Graphen ist ein azyklisch verbundener Untergraph, der alle Scheitelpunkte enthält, ein gewichteter Graph. Der minimale Spannbaum von ist sein Spannbaum mit dem geringsten Gewicht.

Prim-Algorithmus

Eine kurze Beschreibung des Algorithmus

1). Eingabe: ein gewichteter zusammenhängender Graph, wobei die Scheitelpunktmenge V und die Kantenmenge E ist;

2). new _{= {x}, wobei x ein beliebiger Knoten (Startpunkt) in der Menge V ist, E}new _{= {}, leer ist}

3) Wiederholen Sie die folgenden Operationen, bis Vneu _{= V:}

a mit dem kleinsten Gewicht Menge E, wobei u die Menge der Elemente in Vneu _{ist und v nicht in der Menge V}neu _{ist, und v∈V (wenn es mehrere Kanten gibt, die die oben genannten Bedingungen erfüllen , das heißt, das gleiche Gewicht haben, dann wählen Sie eines davon aus); u, v> Kante zur Menge E}neu;

_{4). neu} um den resultierenden minimalen Spannbaum zu beschreiben.

Die folgende Abbildung beschreibt den Algorithmus

Legende

Beschreibung

Nicht optionalOptionalAusgewählt (V--Scheitelpunkt D und D, 7 von A, DB mit einem Abstand von 7 von ACA, D, F

		neu)
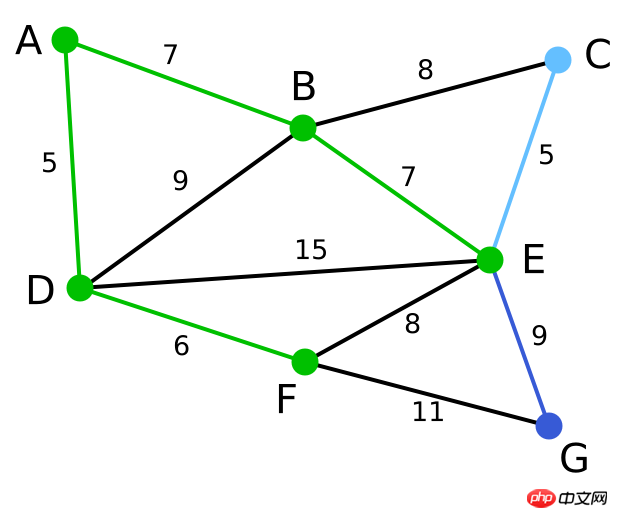
Dies ist das ursprüngliche gewichtete verbundene Diagramm. Die Zahl auf einer Seite jeder Kante gibt ihr Gewicht an. -
wird willkürlich als Ausgangspunkt gewählt. Die Eckpunkte A, B, E	F sind durch eine einzelne Kante mit D verbunden. A ist der Scheitelpunkt, der D am nächsten liegt, daher werden A und die entsprechende Kante AD hervorgehoben. C, GA, B, E, F
Der nächste Scheitelpunkt ist der Abstand D oder A nächster Scheitelpunkt. B ist 9 von D	A, E ist 15 und F ist 6. Daher ist F am nächsten zu D oder A, also sind der Scheitelpunkt F und die entsprechende Kante DF Express hervorgehoben. C, GB, E, F			Der Algorithmus wiederholt weiterhin die oben genannten Schritte. Der Scheitelpunkt
wird hervorgehoben.	B, E, G				In der aktuellen Situation können Sie zwischen C, E und G wählen. Der Abstand zwischen C und B beträgt 8, der Abstand zwischen E und B beträgt 7 und der Abstand zwischen G und F ist 11. E ist am nächsten, daher werden der Scheitelpunkt E und die entsprechende Kante BE hervorgehoben.	Keine	C, E, G	A, D, F, B
	Hier gibt es Optionen dazu Wählen Sie aus Die Eckpunkte sind nur C und G. Der Abstand zwischen C und E beträgt 5, und der Abstand zwischen G und E beträgt 9, also wählen Sie C und verschmelzen Sie es mit der Seite EC werden gemeinsam hervorgehoben.	Keine	C, G	A, D, F, B, E
	VertexG ist der einzige links Der Scheitelpunkt liegt 11 von F, 9 von E und E ist am nächsten, daher wird er hervorgehoben, um G anzuzeigen die entsprechende KanteEG.	Keine	G	A, D, F, B, E, C
	Jetzt wurden alle Eckpunkte ausgewählt, grün im Bild Der Teil ist der minimale Spannbaum des verbundenen Diagramms. In diesem Beispiel beträgt die Summe der Gewichte des minimalen Spannbaums 39.	Keine	Keine	A, D, F, B, E, C, G

Informationen zur Algorithmusimplementierung finden Sie in der vierten Ausgabe von „Algorithmus“ oder „Datenstruktur – Java-Sprachimplementierung“ von Tsinghua Publishing House (die Implementierungsmethode ist klarer und einfacher)

Kruskal-Algorithmus

1. Übersicht

Kruskals Algorithmus ist ein Algorithmus zur Ermittlung des minimalen aufspannenden Baums, der 1956 von Joseph Kruskal veröffentlicht wurde. Es gibt auch den Prim-Algorithmus und den Boruvka-Algorithmus, die zur Lösung desselben Problems verwendet werden. Alle drei Algorithmen sind Anwendungen gieriger Algorithmen. Der Unterschied zum Boruvka-Algorithmus besteht darin, dass der Kruskal-Algorithmus auch dann wirksam ist, wenn es Kanten mit demselben Gewicht im Diagramm gibt.

2. Einfache Beschreibung des Algorithmus

1 ). Denken Sie daran, dass es in Graph

2) einen neuen Graphen gibt hat das Originaldiagramm. Die gleichen e-Eckpunkte, aber keine Kanten 3). Sortieren Sie alle e-Kanten im Originaldiagramm von klein nach groß nach Gewicht

4). Schleife: Beginnen Sie mit der Kante mit dem geringsten Gewicht und durchlaufen Sie jede Kante, bis sich alle Knoten im Diagramm in derselben verbundenen Komponente befinden

wenn diese Kante verbunden ist Die beiden Knoten im Diagramm Diagrammneu

befinden sich nicht in derselben verbundenen Komponente

Legendenbeschreibung:

Zuerst haben wir im ersten Schritt einen Graphen Graph mit mehreren Punkten und Kanten

Sortieren Sie die Längen aller Kanten und verwenden die sortierten Ergebnisse als Grundlage für unsere Kantenauswahl. Auch hier spiegelt sich die Idee des Greedy-Algorithmus wider.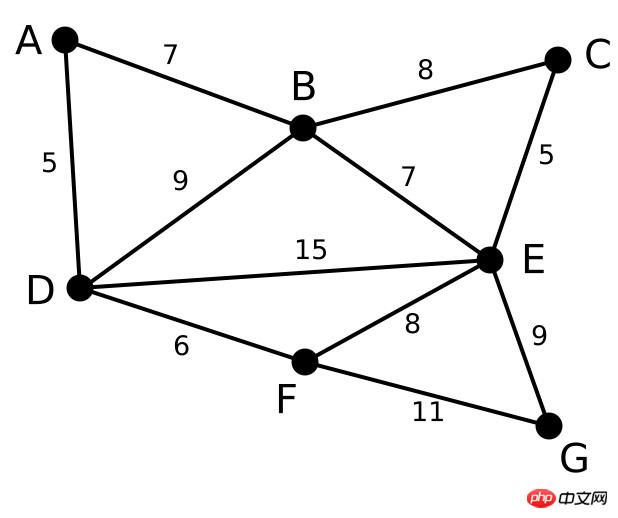

Durch die Ressourcensortierung werden die lokal optimalen Ressourcen ausgewählt. Nachdem die Sortierung abgeschlossen ist, übernehmen wir die Führung bei der Auswahl von Edge AD. Auf diese Weise wird unser Bild zum Bild rechts

Suchen Sie nach den verbleibenden Änderungen. Wir haben CE gefunden. Das Gewicht beträgt hier auch 5

und so finden wir 6, 7, 7, also DF, AB, BE.

Wählen Sie weiterhin BC oder EF aus, obwohl die Seite mit der Länge 8 jetzt die kleinste nicht ausgewählte Seite ist. Aber jetzt sind sie verbunden (BC kann über CE, EB verbunden werden,

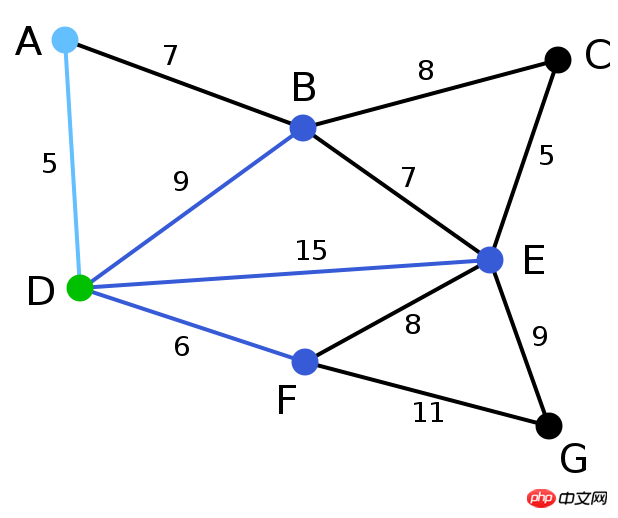
ähnlich EF kann über EB, BA, AD, DF verbunden werden). Sie müssen sie also nicht auswählen. Ähnliche BDs sind ebenfalls angeschlossen (die Verbindungslinien im Bild oben sind rot dargestellt). Am Ende bleiben nur noch EG und FG übrig. Natürlich haben wir uns für EG entschieden.

Informationen zur Algorithmusimplementierung finden Sie im Code in der vierten Ausgabe von „Algorithmus“.

Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung von Beispielen für minimal aufspannende Bäume. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!