Kann Python partielle Differentialgleichungen lösen?

fipy

菲克定律是指在不依靠宏观的混合作用发生的传质现象时，描述分子扩散过程中传质通量与浓度梯度之间关系的定律。菲克定律是阿道夫·菲克（Adolf Fick）于1855年提出。

由菲克第二定律可以得到动态扩散的偏微分方程。求解可以得到浓度分布和流出曲线。

不确定这个问题有没有解析解，不过数值求解是一种较为通用的解决方法。

fipy是目前难得的还活着的PDE求解python包，作者根据官方示例改写本程序。

相关推荐：《python视频教程》

问题

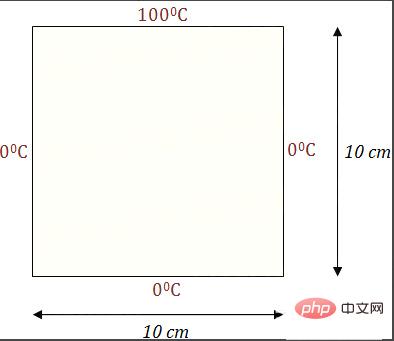
一个二维平板，顶端1摄氏度（100也可以，只是一个系数），另外三个边缘0摄氏度，初始时刻整个板子都是0摄氏度，随之时间的推进，热量在板子上传递，最后达到平衡态，我们不仅希望知道平衡态的温度分布，也希望知道温度随时间是如何变化的。热量的传递由微分方程给出，可以简单地理解为热量按照温度降低最快的方向进行传递。

公式右边是温度的梯度，左边是温度随时间的变化

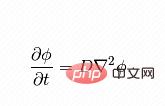
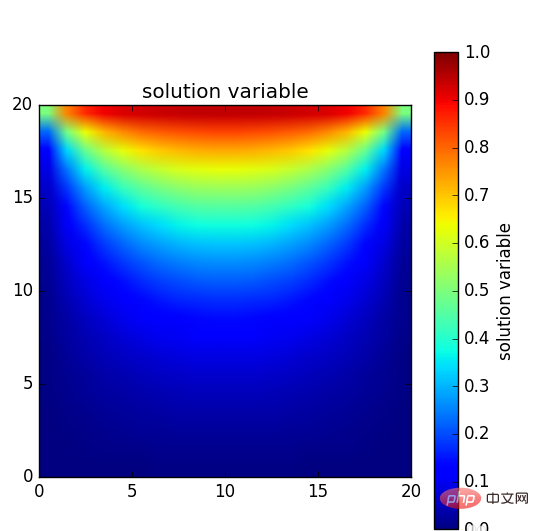
最后整个板子的温度分布大致呈现怎样

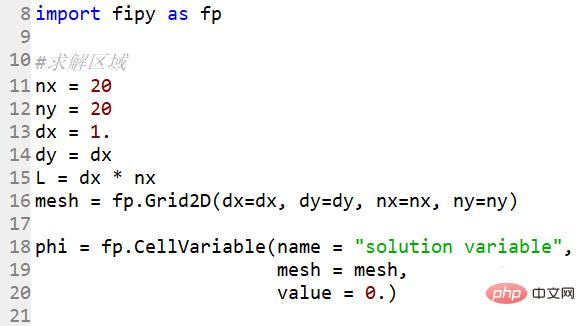
只有一个包需要导入

import fipy as fp

确定求解区域，一个20*20的格点

#求解区域nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)

phi = fp.CellVariable(name = "solution variable",                      mesh = mesh,                      value = 0.)

创建微分方程

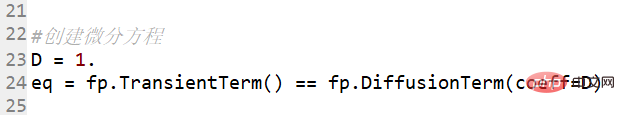
设立边界条件

创建画图

求解

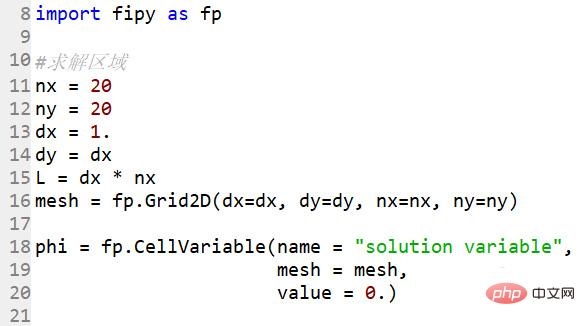
建议在命令行里面运行，命令行里面可以获得动图，ipython里面只有最后一张图

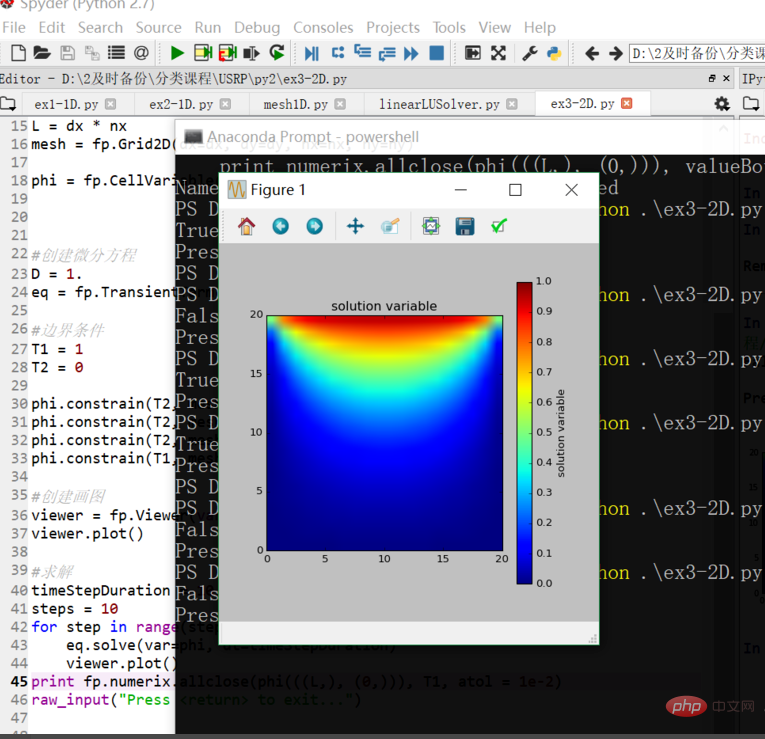
spyder的ipython里面只有最后的一张图片

Das obige ist der detaillierte Inhalt vonKann Python partielle Differentialgleichungen lösen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!