js_Drei Algorithmen für die Binärbaumdurchquerung in der vorderen, mittleren und hinteren Reihenfolge_Implementierung eines einfachen Binärbaums

Über die Einrichtung und Durchquerung von Binärbäumen gibt dieser Artikel eine detaillierte Einführung sowie die Algorithmen für die Durchquerung von Binärbäumen vor der Bestellung, die Durchquerung von Binärbäumen in der Reihenfolge und die Durchquerung von Binärbäumen nach der Bestellung Wird auch zitiert, um es für jeden einfacher zu machen, es klarer zu sehen. Die Einleitung dieses Artikels sollte zum leichteren Verständnis mit Binärbäumen und binären Suchbäumen beginnen. Apache PHP MySQL

Binärbaum und binärer Suchbaum

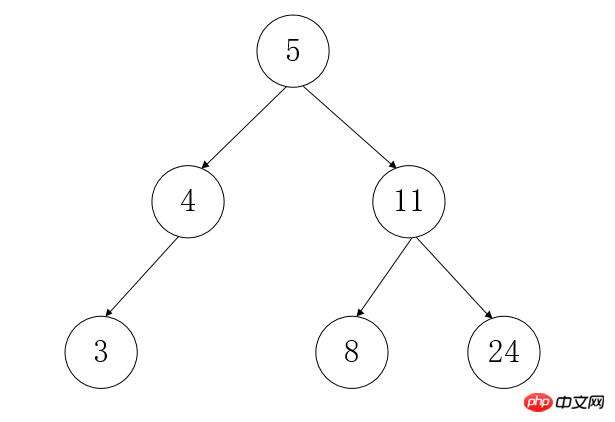
Verwandte Begriffe zum Baum:

Knoten: Jedes Element im Baum ein Knoten,

Wurzelknoten: ein Knoten, der sich am Scheitelpunkt des gesamten Baums befindet, er hat keinen übergeordneten Knoten, wie in Abbildung 5 oben gezeigt

untergeordneter Knoten: Nachkommen anderer Knoten

Blätterknoten: Elemente ohne untergeordnete Knoten werden Blattknoten genannt, wie in Abbildung 3 8 24 dargestellt

Binärbaum: Ein Binärbaum ist eine Datenstruktur und seine organisatorische Beziehung ähnelt einem Baum in der Natur . Die Definition in der offiziellen Sprache lautet: Es handelt sich um eine Menge endlicher Elemente, die entweder leer ist oder aus einem Element namens Wurzel und zwei disjunkten Binärbäumen besteht, die als linker Teilbaum bzw. rechter Teilbaum bezeichnet werden.

Binärer Suchbaum:
Der binäre Suchbaum wird auch als binärer Suchbaum (BST) bezeichnet. Er erlaubt uns nur, einen kleineren Wert im linken Knoten als im übergeordneten Knoten und einen kleineren Wert im zu speichern Für größere Werte zeigt das Bild oben einen binären Suchbaum.

Code-Implementierung

Erstellen Sie zunächst eine Klasse zur Darstellung eines binären Suchbaums. Darin sollte sich eine Node-Klasse befinden, um Knoten zu erstellen

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
    }

Sie sollte auch eine Methode haben:

• insert(key) Einen neuen Schlüssel einfügen

• inOrderTraverse() Durchlaufen des Baums in der richtigen Reihenfolge durchführen und das Ergebnis ausdrucken

• preOrderTraverse() führt eine Vorbestellungsdurchquerung des Baums durch und gibt das Ergebnis aus.

• postOrderTraverse() führt eine Nachbestellungsdurchquerung des Baums durch und gibt das Ergebnis aus Ergebnis

• search(key) sucht nach dem Schlüssel im Baum, gibt true zurück, wenn er existiert, gibt fasle zurück, wenn er nicht existiert

• findMin() gibt den minimalen Wert im Baum zurück

• findMax() gibt den maximalen Wert im Baum zurück

• remove(key) löscht a Geben Sie einen Schlüssel in den Baum ein

Fügen Sie einen Schlüssel in den Baum ein

Fügen Sie einen neuen Schlüssel in den Baum ein. Die Homepage sollte eine Node-Klasseninstanz erstellen, um den neuen Knoten darzustellen. Sie müssen also die Node-Klasse neu erstellen und übergeben. Der einzufügende Schlüsselwert wird automatisch auf einen neuen Knoten mit null linken und rechten Knoten initialisiert.

Dann müssen zunächst einige Beurteilungen vorgenommen werden , beurteilen Sie, ob der Baum leer ist, wird der neu eingefügte Knoten als Wurzel verwendet. Wenn der Knoten nicht leer ist, rufen Sie eine Hilfsmethode insertNode() auf und übergeben Sie den Wurzelknoten und den neuen Knoten an

    this.insert = function(key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
        } else {
            insertNode(root, newNode)
        }
    }

Definieren Sie die Methode insertNode(). Diese Methode ruft sich selbst rekursiv auf, um den neuen Knoten zu finden.

    var insertNode = function(node, newNode) {
        if (newNode.key <= node.key) {
            if (node.left === null) {
                node.left = newNode
            }else {
                insertNode(node.left, newNode)
            }
        }else {
            if (node.right === null) {
                node.right = newNode
            }else {
                insertNode(node.right, newNode)
            }
        }
    }

Vervollständigen Sie die In-Order-Traversal-Methode.

Um die In-Order-Traversierung zu implementieren, benötigen wir eine inOrderTraverseNode(node)-Methode, die sich selbst rekursiv aufrufen kann, um jeden Knoten zu durchlaufen

    this.inOrderTraverse = function() {
        inOrderTraverseNode(root)
    }

Diese Methode gibt den Schlüsselwert jedes Knotens aus. Sie erfordert eine rekursive Beendigungsbedingung - Überprüfen Sie, ob der eingehende Knoten null ist. Rufen Sie sich weiterhin rekursiv auf, um die linke und linke Seite des Knotens zu überprüfen. Der rechte Knoten ist ebenfalls sehr einfach zu implementieren:

    var inOrderTraverseNode = function(node) {
        if (node !== null) {
            inOrderTraverseNode(node.left)
            console.log(node.key)
            inOrderTraverseNode(node.right)
        }
    }

Vorbestellungsdurchquerung, Nachbestellungsdurchquerung

Mit der In-Order-Durchquerungsmethode müssen Sie nur geringfügige Änderungen vornehmen, um Vorbestellungsdurchquerung und Nachbestellungsdurchquerung zu erreichen

Der obige Code:

Auf diese Weise kann der gesamte Baum der Reihe nach durchlaufen werden

    // 实现先序遍历
    this.preOrderTraverse = function() {
        preOrderTraverseNode(root)
    }
    var preOrderTraverseNode = function(node) {
        if (node !== null) {
            console.log(node.key)
            preOrderTraverseNode(node.left)
            preOrderTraverseNode(node.right)
        }
    }

    // 实现后序遍历
    this.postOrderTraverse = function() {
        postOrderTraverseNode(root)
    }
    var postOrderTraverseNode = function(node) {
        if (node !== null) {
            postOrderTraverseNode(node.left)
            postOrderTraverseNode(node.right)
            console.log(node.key)
        }
    }

Haben Sie festgestellt, dass die internen Anweisungen die vordere und hintere Position ändern? Drei Durchlaufregeln: Durchlauf vor der Ordnung (Wurzel-Links-Rechts), Durchlauf mittlerer Ordnung (Links-Wurzel-rechts), Durchlauf mittlerer Ordnung (Links-Rechts-Wurzel)

Machen Sie es zuerst. Lassen Sie uns testen it

Der vollständige Code lautet jetzt wie folgt:

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
        
        //插入节点
        this.insert = function(key) {
            var newNode = new Node(key)
            if(root === null) {
                root = newNode
            } else {
                insertNode(root, newNode)
            }
        }
        var insertNode = function(node, newNode) {
            if (newNode.key <= node.key) {
                if (node.left === null) {
                    node.left = newNode
                }else {
                    insertNode(node.left, newNode)
                }
            }else {
                if (node.right === null) {
                    node.right = newNode
                }else {
                    insertNode(node.right, newNode)
                }
            }
        } 
        
        //实现中序遍历
        this.inOrderTraverse = function() {
            inOrderTraverseNode(root)
        }
        var inOrderTraverseNode = function(node) {
            if (node !== null) {
                inOrderTraverseNode(node.left)
                console.log(node.key)
                inOrderTraverseNode(node.right)
            }
        }
        // 实现先序遍历
        this.preOrderTraverse = function() {
            preOrderTraverseNode(root)
        }
        var preOrderTraverseNode = function(node) {
            if (node !== null) {
                console.log(node.key)
                preOrderTraverseNode(node.left)
                preOrderTraverseNode(node.right)
            }
        }

        // 实现后序遍历
        this.postOrderTraverse = function() {
            postOrderTraverseNode(root)
        }
        var postOrderTraverseNode = function(node) {
            if (node !== null) {
                postOrderTraverseNode(node.left)
                postOrderTraverseNode(node.right)
                console.log(node.key)
            }
        }
    }

hat die Methode zum Hinzufügen neuer Knoten und zum Durchlaufen tatsächlich abgeschlossen. Testen wir sie:

Definieren Sie ein Array. Es gibt einige Elemente darin

var arr = [9,6,3,8,12,15]

Wir fügen jedes Element in arr entsprechend in den binären Suchbaum ein und drucken dann das Ergebnis aus

    var tree = new BinarySearchTree()
    arr.map(item => {
        tree.insert(item)
    })
    tree.inOrderTraverse()
    tree.preOrderTraverse()
    tree.postOrderTraverse()

Nachdem wir den Code ausgeführt haben, werfen wir zunächst einen Blick auf den eingefügten Knoten Die endgültige Situation des gesamten Baums:

Ausgabeergebnis

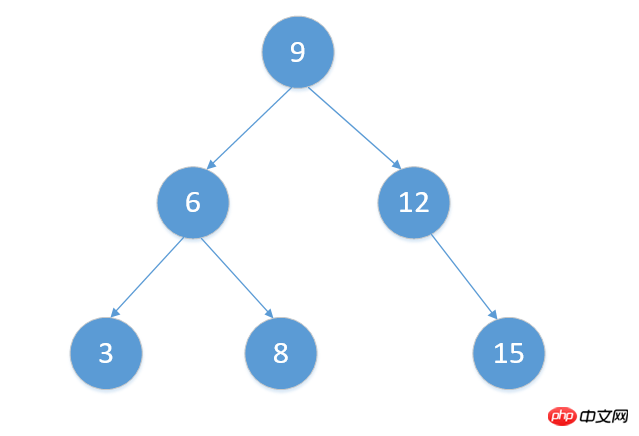
In-order Traversal: <p>3<code><br>3<br>6<br>8<br>9<br>12<br>15<br>6

8

9<br>9<br>6<br>3<br>8<br>12<br>15<br>12

15

<br>3<br>8<br>6<br>15<br>12<br>9<br>Vorbestellungsdurchquerung: <p>9</p>6<h2>3</h2>8<p> 12</p>15<p></p>Durchlauf nach der Bestellung: 3861512 9Offensichtlich ist das Ergebnis wie erwartet, daher verwenden wir den obigen JavaScript-Code, um das Einfügen von Knoten in den Baum und drei Traversierungsmethoden zu implementieren In einem binären Suchbaum ist der Wert des Knotens ganz links am kleinsten und der Wert des Knotens ganz rechts am größten, sodass der binäre Suchbaum leicht die Maximal- und Minimalwerte ermitteln kann. Finden Sie die Minimalwerte und MaximalwerteWie geht das? Tatsächlich müssen Sie nur den Wurzelknoten an die Methode minNode/oder maxNode übergeben und dann durch eine Schleife beurteilen, ob der Knoten links (minNode)/rechts (maxNode) null ist Implementierungscode:

    // 查找最小值
    this.findMin = function() {
        return minNode(root)
    }
    var minNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node.key
        }
        return null
    }
    
    // 查找最大值
    this.findMax = function() {
        return maxNode(root)
    }
    var maxNode = function (node) {
        if(node) {
            while (node && node.right !== null) {
                node =node.right
            }
            return node.key
        }
        return null
    }

所搜特定值

this.search = function(key) {
    return searchNode(root, key)
}

同样，实现它需要定义一个辅助方法,这个方法首先会检验node的合法性，如果为null，直接退出，并返回fasle。如果传入的key比当前传入node的key值小，它会继续递归查找node的左侧节点，反之，查找右侧节点。如果找到相等节点，直接退出，并返回true

    var searchNode = function(node, key) {
        if (node === null) {
            return false
        }
        if (key < node.key) {
            return searchNode(node.left, key)
        }else if (key > node.key) {
            return searchNode(node.right, key)
        }else {
            return true
        }
    }

移除节点

移除节点的实现情况比较复杂，它会有三种不同的情况：

• 
  

• 需要移除的节点是一个叶子节点

• 需要移除的节点包含一个子节点

• 需要移除的节点包含两个子节点

和实现搜索指定节点一元，要移除某个节点，必须先找到它所在的位置，因此移除方法的实现中部分代码和上面相同：

    // 移除节点
    this.remove = function(key) {
        removeNode(root,key)
    }
    var removeNode = function(node, key) {
        if (node === null) {
            return null
        }
        if (key < node.key) {
            node.left = removeNode(node.left, key)
            return node
        }else if(key > node.key) {
            node.right = removeNode(node.right,key)
            return node
        }else{
            //需要移除的节点是一个叶子节点
            if (node.left === null && node.right === null) {
                node = null
                return node
            }
            //需要移除的节点包含一个子节点
            if (node.letf === null) {
                node = node.right
                return node
            }else if (node.right === null) {
                node = node.left
                return node
            }
            //需要移除的节点包含两个子节点
            var aux = findMinNode(node.right)
            node.key = aux.key
            node.right = removeNode(node.right, axu.key)
            return node
        }
    }
    var findMinNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node
        }
        return null
    }

其中，移除包含两个子节点的节点是最复杂的情况，它包含左侧节点和右侧节点，对它进行移除主要需要三个步骤：

1. 需要找到它右侧子树中的最小节点来代替它的位置

2. 将它右侧子树中的最小节点移除

3. 将更新后的节点的引用指向原节点的父节点

有点绕儿，但必须这样，因为删除元素后的二叉搜索树必须保持它的排序性质

测试删除节点

tree.remove(8)
tree.inOrderTraverse()

打印结果：

3<br>6<br>9<br>12<br>15<br>

8 这个节点被成功删除了，但是对二叉查找树进行中序遍历依然是保持排序性质的

到这里，一个简单的二叉查找树就基本上完成了，我们为它实现了，添加、查找、删除以及先中后三种遍历方法

存在的问题

但是实际上这样的二叉查找树是存在一些问题的，当我们不断的添加更大/更小的元素的时候，会出现如下情况：

tree.insert(16)
tree.insert(17)
tree.insert(18)

来看看现在整颗树的情况：

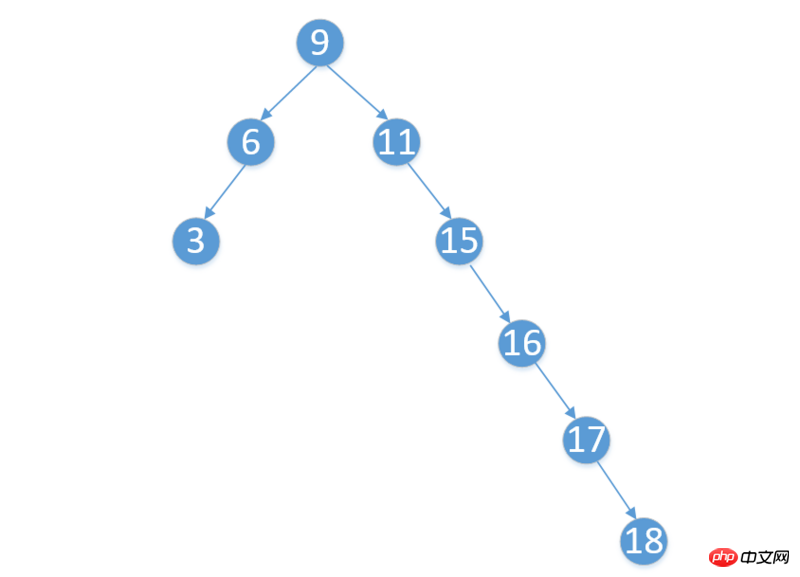
看图片容易得出它是不平衡的，这又会引出平衡树的概念，要解决这个问题，还需要更复杂的实现，例如：AVL树，红黑树 哎，之后再慢慢去学习吧

相关文章：

二叉树遍历算法-php的示例

二叉树的中序遍历,该怎么解决

Das obige ist der detaillierte Inhalt vonjs_Drei Algorithmen für die Binärbaumdurchquerung in der vorderen, mittleren und hinteren Reihenfolge_Implementierung eines einfachen Binärbaums. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!