So zeichnen Sie ein Polygon basierend auf zufälligen Punkten auf der Leinwand

In diesem Artikel werden hauptsächlich die relevanten Informationen zum Zeichnen eines Polygons basierend auf zufälligen Punkten auf der Leinwand vorgestellt. Ich werde ihn jetzt mit Ihnen teilen und als Referenz verwenden.

Ursache

Als ich heute das Buch „HTML5+Javascript Animation Basics“ studierte, habe ich im dritten Abschnitt des Kapitels darüber gesprochen 8 Erfahren Sie, wie Sie mit drei Federn drei Punkte verbinden, um Dehnübungen durchzuführen.

Nachdem ich das Beispiel beendet hatte, dachte ich darüber nach, was wäre, wenn es vier oder fünf Punkte wären.

Ich habe den Code umgeschrieben, um die Anzahl der Punkte variabel zu machen. Der Endeffekt besteht darin, die endgültige Streckbewegung jedes Punktes zum Ausgleichen zu erreichen, aber die Verbindungen zwischen den Punkten sehen nicht sehr gut aus und einige sind gekreuzt.

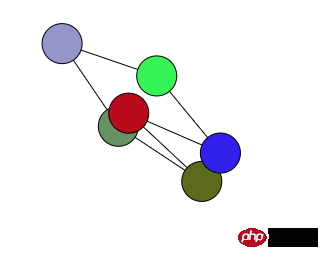
Also habe ich darüber nachgedacht, ob dieser Bereich optimiert werden könnte.

Drehen Sie die Verbindung

Die Punkte im vorherigen Beispiel befinden sich alle an zufälligen Positionen, sodass die Verbindung unkontrollierbar ist. Deshalb möchte ich zunächst damit beginnen.

Verwenden Sie zunächst einen bestimmten Punkt als Referenzpunkt, um die Winkel anderer Punkte relativ zu diesem Punkt zu ermitteln.

Verbinden Sie dann diese Punkte entsprechend dem Winkel von klein nach groß, sodass Sie ein normales Polygon zeichnen können.

Der ungefähre Implementierungscode lautet wie folgt:

let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
  let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
  ball.x = Math.random() * width;
  ball.y = Math.random() * height;
  balls.push(ball)

  if (!firstBall) {
    firstBall = ball
    ball.angle = 0
  } else {
    const dx = ball.x - firstBall.x,
          dy = ball.y - firstBall.y;

    ball.angle = Math.atan2(dy, dx);
  }
}

// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
  return ballA.angle - ballB.angle
})

Auf diese Weise kann das Array beim Zeichnen der Verbindung am Ende durchlaufen werden um den Winkel von klein nach groß zu zeichnen.

Der Effekt ist wie folgt:

Dies kann die Anzahl der sich kreuzenden Linien erheblich reduzieren, kann aber dennoch nicht vollständig vermieden werden.

Als nächstes möchte ich versuchen, diese Lösung zu optimieren, indem ich beispielsweise Math.abs verwende, um den Winkel zu korrigieren, oder den Punkt mit dem kleinsten Winkel finde, um jeden Punkt zu verbinden. Aber das Ergebnis ist nicht gut, Grenzüberschreitungen lassen sich nicht vermeiden.

Rotation basierend auf dem Mittelpunkt

Später ist mir eine andere Idee eingefallen: Wenn der Mittelpunkt des Polygons bestimmt werden kann, dann alle Punkte relativ zum Mittelpunkt werden separat berechnet. Der Winkel zwischen den Punkten kann verwendet werden, um diese Punkte im Uhrzeigersinn oder gegen den Uhrzeigersinn zu verbinden.

Aber nach langer Online-Suche benötigen alle Punktalgorithmen eine Reihe von Punkten, die in einer bestimmten Reihenfolge im Uhrzeigersinn angeordnet sind.

Aber wenn ich diese Punkte habe, kann ich schon ein Polygon zeichnen. Ich musste aufgeben

X-Achsen-Zweipolsegmentierung

In meiner Verzweiflung musste ich bei Google suchen und dann fand ich eine Die Antwort auf Zhihu war ziemlich gut: Wie verbinde ich eine ungeordnete Menge von Punkten auf der Ebene zu einem einfachen Polygon?

Für die spezifische Algorithmusbeschreibung schauen Sie sich einfach die Antwort an und ich werde nicht auf Details eingehen.

Wenn Sie jedoch die obere Kette und die untere Kette verbinden, müssen Sie tatsächlich nur sicherstellen, dass die obere Kette in absteigender Reihenfolge auf der X-Achse verbunden ist und die untere Kette in aufsteigender Reihenfolge verbunden ist der X-Achse (gegen den Uhrzeigersinn gezeichnet). Bei den Punkten mit der gleichen X-Achse spielt es keine Rolle, ob die Y-Achse größer oder kleiner ist.

Bei der Implementierung erfolgt die Implementierung streng nach dem Algorithmus in der Antwort.

Bei der Beurteilung, ob ein Punkt zur oberen oder unteren Kette gehört, besteht die anfängliche Idee darin, die Funktionsgleichung der geraden Linie basierend auf zwei Punkten zu bestimmen und dann die Koordinaten der Punkte zur Berechnung einzuführen. Später dachte ich jedoch, dass alle Punkte den am weitesten links stehenden Pol verwenden, um den Schrägwinkel zu berechnen, und ihn dann entsprechend der Winkelgröße dividieren, was visuell einfacher zu verstehen ist.

Der ungefähre Code lautet wie folgt:

let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;

while(ballNum--) {
  let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
  ball.x = Math.random() * width;
  ball.y = Math.random() * height;
  tempBalls.push(ball)
}

// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
  return ballA.x - ballB.x
})

// 找X轴左右极点
let firstBall = tempBalls[0],
    lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
    bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)

// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
  smallXBalls.sort((ballA, ballB) => {
    return ballB.y - ballA.y
  })
}
if (bigXBalls.length > 1) {
  bigXBalls.sort((ballA, ballB) => {
    return ballB.y - ballA.y
  })
}

firstBall = smallXBalls[0]
lastBall = bigXBalls[0]

// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
    lowerBalls = [];

// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
  if (ball === firstBall || ball === lastBall) {
    return false
  }
  let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
  if (angle > splitLineAngle) {
    lowerBalls.push(ball)
  } else {
    upperBalls.push(ball)
  }
})

// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
  if (ballA.x !== ballB.x) {
    return ballA.x - ballB.x
  }
  return ballB.y - ballA.y
})

upperBalls = upperBalls.sort((ballA, ballB) => {
  if (ballA.x !== ballB.x) {
    return ballB.x - ballA.x
  }
  return ballB.y - ballB.x
})

// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)

balls = balls.map((ball, i) => {
  ball.text = i + 1;
  return ball
})

Die schließlich zurückgegebenen Kugeln sind die Punkte des Polygons, sortiert gegen den Uhrzeigersinn.

Der Effekt ist wie folgt:

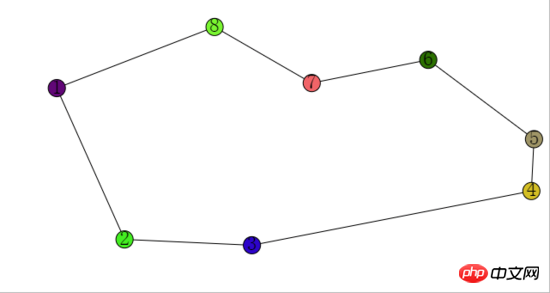
Der innere Zustand jeder Kugel ist wie folgt:

Das Obige ist die Zusammenfassung dieses Artikels. Ich hoffe, dass er für das Studium aller hilfreich ist. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website!

Verwandte Empfehlungen:

Verwenden Sie HTML5 Canvas kapselt ein Kreisdiagramm, das Echarts nicht implementieren kann

HTML5 Canvas implementiert die Methode zum Zeichnen von Kurven

Das obige ist der detaillierte Inhalt vonSo zeichnen Sie ein Polygon basierend auf zufälligen Punkten auf der Leinwand. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!