Detaillierte Erläuterung des Einfügens von Rot-Schwarz-Bäumen und Beispiele für Javascript-Implementierungsmethoden

Dieser Artikel führt Sie hauptsächlich in die relevanten Informationen zum Einfügen von Rot-Schwarz-Bäumen sowie in die Javascript-Implementierungsmethode ein. Der Artikel stellt ihn anhand von Beispielcodes ausführlich vor Es braucht Arbeit. Schauen wir es uns gemeinsam an.

Eigenschaften von rot-schwarzen Bäumen

Ein binärer Suchbaum, der die folgenden Eigenschaften erfüllt, ist ein rot-schwarzer Baum

1. Jeder Knoten ist entweder schwarz oder rot.

2. Der Wurzelknoten ist schwarz.

3. Jeder Blattknoten (NIL) ist schwarz.

4. Wenn ein Knoten rot ist, sind beide untergeordneten Knoten schwarz.

5. Für jeden Knoten enthält der einfache Pfad vom Knoten zu allen seinen untergeordneten Blattknoten die gleiche Anzahl schwarzer Knoten.

Eigenschaft 1 und 2 müssen nicht allzu ausführlich erklärt werden.

Eigenschaft 3, jeder Blattknoten (NIL) ist schwarz. Die Blattknoten beziehen sich hier nicht auf die Knoten 1, 5, 8 und 15 in der obigen Abbildung, sondern auf die Knoten mit Nullwerten in der folgenden Abbildung. Ihre Farbe ist schwarz und sie sind die untergeordneten Knoten ihrer übergeordneten Knoten . .

Eigenschaft 4: Wenn ein Knoten rot ist (im Bild wird Weiß anstelle von Rot verwendet), sind seine beiden untergeordneten Knoten schwarz, z. B. Knoten 2, 5. 8,15. Wenn jedoch beide untergeordneten Knoten eines Knotens schwarz sind, ist der Knoten möglicherweise nicht rot, z. B. Knoten 1.

Eigenschaft 5: Für jeden Knoten enthält der einfache Pfad vom Knoten zu allen seinen untergeordneten Blattknoten die gleiche Anzahl schwarzer Knoten. Beispielsweise beträgt die Anzahl der schwarzen Knoten auf dem einfachen Pfad von Knoten 2 zu allen seinen untergeordneten Blattknoten 2; auf dem einfachen Pfad von Wurzelknoten 11 zu allen seinen untergeordneten Blattknoten beträgt die Anzahl der schwarzen Knoten 2 .

Was sind die Merkmale eines solchen Baumes?

Durch die Einschränkung der Farbe jedes Knotens auf jedem einfachen Pfad von der Wurzel bis zum Blattknoten stellt der Rot-Schwarz-Baum sicher, dass kein Pfad doppelt so lang ist wie jeder andere Pfad es ist annähernd ausgeglichen. ——"Einführung in Algorithmen"

Aufgrund von Eigenschaft 4 liegen zwei rote Knoten in einem rot-schwarzen Baum nicht nebeneinander. Der kürzestmögliche Pfad im Baum ist der Pfad mit allen schwarzen Knoten, und der längstmögliche Pfad im Baum ist der Pfad mit abwechselnd roten und schwarzen Knoten. In Kombination mit Eigenschaft 5 enthält jeder Pfad die gleiche Anzahl schwarzer Knoten, sodass der Rot-Schwarz-Baum sicherstellt, dass kein Pfad doppelt so lang ist wie andere Pfade.

Einfügung eines rot-schwarzen Baums

Fügen Sie zuerst den Knoten in den binären Suchbaum ein und färben Sie ihn rot. Wenn es schwarz ist, verstößt es gegen Eigenschaft 5 und ist unpraktisch anzupassen. Wenn es rot ist, verstößt es möglicherweise gegen Eigenschaft 2 oder Eigenschaft 4. Durch relativ einfache Vorgänge kann es auf die Eigenschaften eines rot-schwarzen Baums zurückgesetzt werden.

Nachdem ein Knoten in einen binären Suchbaum eingefügt wurde, können die folgenden Situationen auftreten:

Fall 1

Nachdem der Knoten vorhanden ist Eingefügt, es gibt keinen übergeordneten Knoten, und der Knoten wird eingefügt, um zum Stammknoten zu werden, was gegen Eigenschaft 2 verstößt. Der Knoten wird auf Schwarz angepasst, um die Einfügung abzuschließen.

Fall 2

Nach dem Einfügen eines Knotens ist sein übergeordneter Knoten schwarz und verletzt keine Eigenschaften. Es ist keine Anpassung erforderlich und das Einfügen ist abgeschlossen. Fügen Sie beispielsweise Knoten 13 in die folgende Abbildung ein.

Fall 3

Nach dem Einfügen eines Knotens ist dessen übergeordneter Knoten rot, was gegen Eigenschaft 4 verstößt und eine Reihe von Anpassungen erfordert. Fügen Sie beispielsweise Knoten 4 in die folgende Abbildung ein.

Was sind also die Anpassungsreihen?

Wenn der übergeordnete Knotenvater des eingefügten Knotenknotens rot ist, muss der Knotenvater einen schwarzen übergeordneten Knotengroßvater haben, denn wenn der Knotenvater keinen übergeordneten Knoten hat, ist er die Wurzel Knotenpunkt und der Wurzelknoten ist schwarz. Dann kann der andere untergeordnete Knoten des Knotengroßvaters als Knotenonkel bezeichnet werden, der der Geschwisterknoten des Knotenvaters ist. Der Knotenonkel kann schwarz oder rot sein.

Lassen Sie uns zunächst die einfachste Situation analysieren, denn komplexe Situationen können in einfache Situationen umgewandelt werden. Die einfache Situation ist die Situation, in der der Knotenonkel schwarz ist.

Fall 3.1

Wie in (a) oben gezeigt, ist die Situation wie folgt: Knoten ist rot, Vater ist rot, Großvater und Onkel sind schwarz , α , β, θ, ω und η sind alle Teilbäume, die den Knoten entsprechen. Nehmen Sie an, dass im gesamten binären Suchbaum aufgrund der Verletzung von Eigenschaft 4 nur Knoten und Vater kein normaler Rot-Schwarz-Baum werden können. Zu diesem Zeitpunkt kann durch Anpassen von Bild (a) an Bild (b) ein normaler Rot-Schwarz-Baum wiederhergestellt werden. schwarzer Baum. Der gesamte Anpassungsprozess gliedert sich eigentlich in zwei Schritte: Drehung und Farbwechsel.

Was ist Rotation?

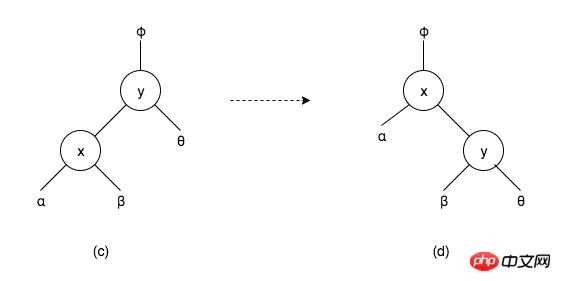
Wie in der Abbildung (c) oben gezeigt, ist es Teil eines binären Suchbaums, wobei x, y Knoten und α, β, θ die Teilbäume der entsprechenden Knoten sind . Aus der Abbildung ist ersichtlich, dass α < x < y, das heißt, alle Knoten im α-Teilbaum sind kleiner als der Wert von Knoten y, und der Wert des Knotens y ist kleiner als der aller Knoten im θ-Teilbaum. Wenn in einem binären Suchbaum der Wert von Knoten y größer als der Wert von Knoten x ist, befindet sich Knoten x im linken Teilbaum von Knoten y, wie in Abbildung (c) gezeigt Knoten x Im rechten Teilbaum, wie in Abbildung (d) gezeigt. Daher kann α < x < y < Dies ist eine Rotation, die die Eigenschaften binärer Suchbäume nicht zerstört.

Knoten ist rot, Vater ist rot, Großvater und Onkel sind schwarz. Spezifische Situation 1

In Abbildung (a) ist Knoten der linke untergeordnete Knoten des Vaters und Vater ist das linke Kind von Grand. Knoten < In diesem Fall kann „Vater < Grand“ ausgedrückt werden als „Vater“ ist der linke Teilbaum von „Grand“ oder „Grand“ ist der rechte Teilbaum von „Vater“. Daher werden „Vater“ und „Grand“ in Abbildung (a) gedreht Die Rotation zerstört nicht die Eigenschaften eines binären Suchbaums, aber nach der Rotation werden die Eigenschaften eines rot-schwarzen Baums zerstört, sodass die Farbe der Knoten angepasst werden muss.

Farbänderung

Nachdem das Bild (a) gedreht wurde, sollte der Flügel in Rot geändert werden, der Vater sollte in Schwarz geändert werden und es wird zum Bild (b). Schließen Sie die Einfügung ab.

Knoten ist rot, Vater ist rot, Großvater und Onkel sind schwarz. Spezifische Situation 2

Knoten ist der rechte untergeordnete Knoten von Vater und Vater ist der rechte untergeordnete Knoten von Grand, wie gezeigt Unten (e) ist die Umkehrung der spezifischen Situation 1.

Das heißt, Onkel < Grand < Vater < (f), um die Einfügung abzuschließen.

Knoten ist rot, Vater ist rot, Großvater und Onkel sind schwarz. Spezifische Situation drei

Knoten ist der rechte untergeordnete Knoten von Vater und Vater ist der linke untergeordnete Knoten von Grand, wie gezeigt unten (m).

Nachdem der Knoten und der Vater in Abbildung (m) gedreht wurden, wird er zu Abbildung (n), und die Behandlung des Vaters als neuer Knoten wird nach der Drehung erneut zur spezifischen Situation und die Farbe ändern, ist die Einfügung abgeschlossen.

Knoten ist rot, Vater ist rot, Großvater und Onkel sind schwarz. Spezifische Situation vier

Knoten ist der rechte untergeordnete Knoten von Vater und Vater ist der linke untergeordnete Knoten von Grand, wie gezeigt Unten (i) ist die Umkehrung der spezifischen Situation drei.

Nachdem der Knoten und der Vater in Abbildung (i) gedreht wurden, wird er zu Abbildung (j), und die Behandlung des Vaters als neuer Knoten wird zur spezifischen Situation 2. Nochmals nach der Drehung und die Farbe ändern, ist die Einfügung abgeschlossen.

Fall 3.2

Knoten, Vater und Onkel sind rot, Großvater ist schwarz.

Wie im Bild oben (k) gezeigt, ist der Flügel nicht rotierend, sondern rot gefärbt, Vater und Onkel sind schwarz und der Flügel wird als neuer verwendet Knoten, um die Situation zu beurteilen. Wenn Grand als neuer Knoten verwendet wird, wird er zu Fall 2 und die Einfügung wird abgeschlossen. Wenn er zu Fall 3.1 wird, ist die Einfügung nach der Anpassung abgeschlossen. Wenn es sich immer noch um Fall 3.2 handelt, ändern Sie weiterhin die Farbe von Grand, Vater und Onkel und Knoten Der Knoten wird nach oben verschoben. Wenn der neue Knoten keinen übergeordneten Knoten hat, wird er zu Fall 1. Der Wurzelknoten wird schwarz gefärbt und die Einfügung ist abgeschlossen.

Zusammenfassung

td>

	node的情形	操作
情形1	node为红,无father	将node重新着色
情形2	node为红,father为黑
情形3.1	node,father为红,grand,uncle为黑	旋转一次或两次,并重新着色
情形3.2	node,father,uncle为红,grand为黑	将father, uncle,grand重新着色, grand作为新的node

Situation des Knotens

Betrieb

Situation 1

Knoten ist rot, kein Vater

Knoten neu einfärben

Fall 2

Knoten ist rot und Vater ist schwarz

td>

Fall 3.1

Knoten, Vater ist rot, Groß, Onkel ist schwarz

Ein- oder zweimal drehen und neu einfärben

Fall 3.2

Knoten, Vater, Onkel sind rot, Grand ist schwarz

Vater, Onkel, Grand, Grand als neuer Knoten neu einfärben

Code

// 结点
function Node(value) {
 this.value = value
 this.color = 'red' // 结点的颜色默认为红色
 this.parent = null
 this.left = null
 this.right = null
}

function RedBlackTree() {
 this.root = null
}

RedBlackTree.prototype.insert = function (node) {
 // 以二叉搜索树的方式插入结点
 // 如果根结点不存在，则结点作为根结点
 // 如果结点的值小于node，且结点的右子结点不存在，跳出循环
 // 如果结点的值大于等于node，且结点的左子结点不存在，跳出循环
 if (!this.root) {
 this.root = node
 } else {
 let current = this.root
 while (current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;]) {
  current = current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;]
 }
 current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;] = node
 node.parent = current
 }
 // 判断情形
 this._fixTree(node)
 return this
}

RedBlackTree.prototype._fixTree = function (node) {
 // 当node.parent不存在时，即为情形1，跳出循环
 // 当node.parent.color === &#39;black&#39;时，即为情形2，跳出循环
 while (node.parent && node.parent.color !== &#39;black&#39;) {
 // 情形3
 let father = node.parent
 let grand = father.parent
 let uncle = grand[grand.left === father ? &#39;right&#39; : &#39;left&#39;]
 if (!uncle || uncle.color === &#39;black&#39;) {
  // 叶结点也是黑色的
  // 情形3.1
  let directionFromFatherToNode = father.left === node ? &#39;left&#39; : &#39;right&#39;
  let directionFromGrandToFather = grand.left === father ? &#39;left&#39; : &#39;right&#39;
  if (directionFromFatherToNode === directionFromGrandToFather) {
  // 具体情形一或二
  // 旋转
  this._rotate(father)
  // 变色
  father.color = &#39;black&#39;
  grand.color = &#39;red&#39;
  } else {
  // 具体情形三或四
  // 旋转
  this._rotate(node)
  this._rotate(node)
  // 变色
  node.color = &#39;black&#39;
  grand.color = &#39;red&#39;
  }
  break // 完成插入，跳出循环
 } else {
  // 情形3.2
  // 变色
  grand.color = &#39;red&#39;
  father.color = &#39;black&#39;
  uncle.color = &#39;black&#39;
  // 将grand设为新的node
  node = grand
 }
 }

 if (!node.parent) {
 // 如果是情形1
 node.color = &#39;black&#39;
 this.root = node
 }
}

RedBlackTree.prototype._rotate = function (node) {
 // 旋转 node 和 node.parent
 let y = node.parent
 if (y.right === node) {
 if (y.parent) {
  y.parent[y.parent.left === y ? &#39;left&#39; : &#39;right&#39;] = node
 }
 node.parent = y.parent
 if (node.left) {
  node.left.parent = y
 }
 y.right = node.left
 node.left = y
 y.parent = node
 } else {
 if (y.parent) {
  y.parent[y.parent.left === y ? &#39;left&#39; : &#39;right&#39;] = node
 }
 node.parent = y.parent
 if (node.right) {
  node.right.parent = y
 }
 y.left = node.right
 node.right = y
 y.parent = node
 }
}

let arr = [11, 2, 14, 1, 7, 15, 5, 8, 4, 16]
let tree = new RedBlackTree()
arr.forEach(i => tree.insert(new Node(i)))
debugger

Ich habe das Obige für Sie zusammengestellt und hoffe, dass es Ihnen in Zukunft hilfreich sein wird.

Verwandte Artikel:

JS-Ajax-Fortschrittsbarcode beim Laden

Zwei Lösungen für domänenübergreifende Ajax-Probleme Methode

Basierend auf Ajax, klicken Sie, um mehr ohne Aktualisierung zu laden und auf diese Seite zu laden

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Einfügens von Rot-Schwarz-Bäumen und Beispiele für Javascript-Implementierungsmethoden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!