Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend

Dieses Mal werde ich Ihnen ein Beispiel für den Sortieralgorithmus im Frontend ausführlich erläutern. Was sind die Vorsichtsmaßnahmen bei der Verwendung des Sortieralgorithmus im Frontend? Praktischer Fall, werfen wir einen Blick darauf.

Vorwort

Vorgestern habe ich einen Artikel über Zhihu gesehen, in dem er sich über den schnellen Sortieralgorithmus von Lehrer Ruan Yifeng beschwert hat. Ich denke, ohne ihn kann niemand Fehler machen Ich bin davon überzeugt, dass Bücher schlimmer sind als keine Bücher. Wir sollten uns freuen, wenn uns jemand hilft, diesen Fehler zu korrigieren Lehrer Ruan Yifeng lernt und korrigiert auch ständig Fehler, also besteht kein Grund zur Irreführung. Was ist, wenn nicht er den Fehler gemacht hat? JavaScript? Also wird jeder Fehler machen, und wir sollten es auch akzeptieren und immer darüber nachdenken, ob das die optimale Lösung ist und ob es meiner Meinung nach eine bessere Lösung gibt
Und da ich als Front-End-Profi in der Informatik verschiedene Aufgaben nicht gut umsetzen kann, habe ich mich für den auf dieser Idee basierenden Sortieralgorithmus sehr geschämt, also habe ich mir die Zeit genommen, das Buch „Daten“ sorgfältig zu lesen Struktur- und Algorithmusanalyse: C-SpracheBeschreibung + chinesische Version.pdf>> Ich hoffe, dass es Ihnen einige Hinweise und Vorteile geben kann Wenn etwas nicht stimmt, weisen Sie bitte darauf hin, was Ihrer Meinung nach eine bessere Idee ist. Am glücklichsten ist es, gemeinsam zu lernen und Fortschritte zu machen.

1 Seien Sie vertraut mit

1.1 Zeitkomplexität

(1) Das Konzept der Zeitkomplexität
Algorithmus Die Zeitkomplexität ist eine Funktion, die die Laufzeit eines Algorithmus qualitativ beschreibt wird häufig verwendet, mit Ausnahme der Terme niedriger Ordnung und der Termkoeffizienten hoher Ordnung dieser Funktion
(2) Berechnungsmethode

• Im Allgemeinen die Anzahl der Ausführungen grundlegender Operationen in Ein Algorithmus ist eine Funktion der Problemgröße n, dargestellt durch T(n), wenn es eine bestimmte Hilfsfunktion f(n) gibt, sodass bei Annäherung an die Unendlichkeit der Grenzwert von T(n)/f(n) erreicht wird ) eine Konstante ungleich Null ist, dann ist f(n) eine Funktion in der gleichen Größenordnung wie T(n), bezeichnet als T(n) = O(f (n)), nennen Sie O(f(n) ) die asymptotische Zeitkomplexität des Algorithmus, die als Zeitkomplexität bezeichnet wird. Analyse: Wenn Modul n zu jedem Zeitpunkt zunimmt, ist die Wachstumsrate der Ausführungszeit proportional zum Wachstum Rate von f(n), also je kleiner f(n), desto geringer ist die Zeitkomplexität des Algorithmus und desto höher ist die Effizienz des Algorithmus.

• Bei der Berechnung der Zeitkomplexität gilt: Finden Sie zuerst die Grundoperationen des Algorithmus heraus, berechnen Sie dann die Anzahl der Ausführungen der Grundoperationen und finden Sie f(n) in der gleichen Größenordnung wie T(n) (die gleiche Größenordnung hat im Allgemeinen Folgendes: 1 , log₂n , n, nlog₂n, n quadriert, n kubisch), wenn T(n) / f(n) den Grenzwert findet, um eine Konstante c zu erhalten, dann ist die Zeitkomplexität T(n) = O(f(n)):

• Zum Beispiel:

  for(i = 1; iWir können T(n) = n^3 + n^2 erhalten und wir können bestimmen, dass n^3 dasselbe ist wie T(n) Größenordnung, f(n)=n^3; dann ist T(n) / f(n) = 1 + 1/n. Der Grenzwert ist konstant 1, also ist die Zeitkomplexität dieses Algorithmus: 

T(n) = O(n^3);

Hinweis: Der Einfachheit halber verwende ich N, um die Anzahl der Array-Elemente darzustellen.

2 . Sortieralgorithmus

2.1 Blasensortierung

2.1.1 Hauptidee:

Die Hauptidee der Blasensortierung besteht darin, ein Array von zu durchlaufen Die Länge n liegt zwischen n-1 und 1, und der Maximalwert der ersten i-Elemente wird an der i-Position platziert. Stellen Sie sich vor, dass die Blasensortierung eine vertikale Wassersäule ist ​​(schwer) sinkt weiter, kleine Werte (leicht) schweben weiter nach oben, sodass nach Abschluss der Durchquerung der Wert an jeder Position größer als der vorherige Wert ist und die Sortierung abgeschlossen ist.

2.1.2 Zeitkomplexität

Zeitkomplexität im schlimmsten Fall: o(n^2);

Zeitkomplexität im besten Fall: o(n^2);

2.1.3 Darstellung des Sortiervorgangs:

Die Ausgangsschleife im Diagramm dient zum Verlassen der inneren Schleife

2.1.4 代码实现:

冒泡排序-非递归实现

function bubbleSort(arr) {
    for(var i = arr.length - 1; i > 1; i--) {
        for(var j=0; j  arr[j+1]) {
                var temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
bubbleSort(arr);  // [8, 21, 32, 34, 51, 64]

冒泡排序-递归实现

function bubbleSort(arr, n) {
    if(n  arr[j+1]) {
                var temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
        return bubbleSort(arr, --n);
    }
}
var arr =  [34,8,64,51,32,21];
bubbleSort(arr, arr.length);  // [8, 21, 32, 34, 51, 64]

2.2 插入排序

2.2.1 主要思想:

插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要 将 i 位置上的元素 和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.

2.2.2 时间复杂度

最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);

2.2.3 Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend:

图解中的出循环是退出内层循环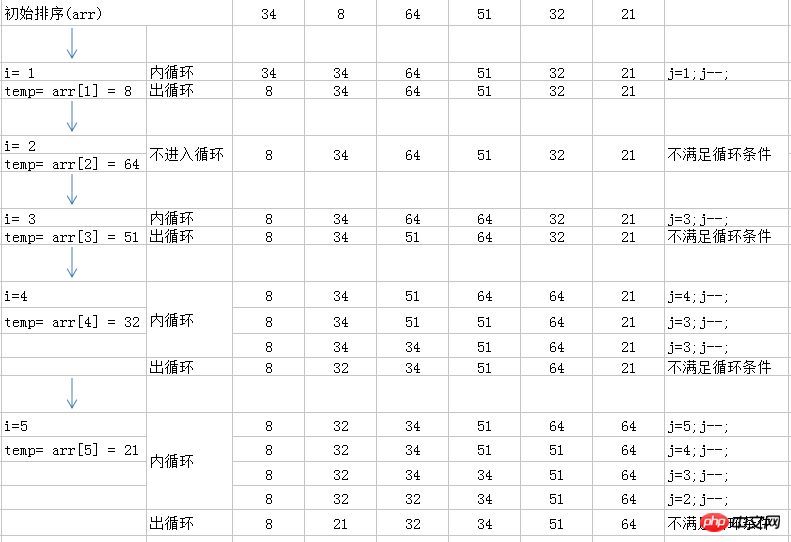

2.2.4 代码实现

插入排序-非递归实现

function insertSort(arr) {
    var n = arr.length,temp = 0;
    for(var i = 1; i  0 && arr[j-1] > temp; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
insertSort(arr);  // [8, 21, 32, 34, 51, 64]

插入排序-递归实现

function insertSort(arr, n) {
    if(n > 0 && n  0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1];
            j--;
        }
        arr[j] = temp;
        i++;
        return insertSort(arr, i);
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1

2.3 快速排序

顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.

2.3.1 基本思想

通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.

2.3.2 实现步骤

第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i第六步: 重复第二步到第四步,依次对i位置左右两边的元素进行快速排序,直到left大于等于right为止.

2.3.3 时间复杂度:

平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

2.3.4 Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend

2.3.5 代码实现:

快速排序-递归实现

function quickSort(arr, left, right) {
    if(left >= right) return;
    var i = left;
    var j = right - 1;
    var privot = arr[left];
    //console.log(privot);
    while(i = privot) j--;
        arr[i] = arr[j];
        while(i<j var quicksort><h4 style="text-align: left;">快速排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function mainProduce(arr, left, right) {
        var i = left, j = right - 1;
        var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
        var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
        var privot = arr[left];
        while(i = privot) j--;
            var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
            while(i<j> left + 1) {
                s.push(left);s.push(mid);
            }
            if(mid  left + 1) {
                    s.push(left);s.push(mid);
                }
                if(mid <h2 style="text-align: left;">2.4 希尔排序</h2>
<h3 style="text-align: left;">2.4.1 主要思想</h3>
<p style="text-align: left;">希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个<a href="http://www.php.cn/code/54.html" target="_blank">数组排序</a>完成,算法终止.</p>
<h3 style="text-align: left;">2.4.2主要步骤</h3>
<p style="text-align: left;">第一步: 选取一个增量d,初始值是Math.floor(len/2);<br>第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;<br>第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.</p>
<p style="text-align: left;">希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.</p>
<h3 style="text-align: left;">2.4.3 时间复杂度</h3>
<p style="text-align: left;">平均情况下的时间复杂度: o(nlog₂n);<br>最好情况下的时间复杂度: o(n);</p>
<h3 style="text-align: left;">2.4.4 Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend</h3>
<p style="text-align: left;"><img src="https://img.php.cn/upload/article/000/061/021/2f13ca0ab50333d1dad5851595e7225d-3.jpg" alt="Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend" title="Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend"></p>
<p style="text-align: left;">图片源于自百度百科: 图片来源</p>
<h3 style="text-align: left;">2.4.5 代码实现:</h3>
<h4 style="text-align: left;">希尔排序-递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr, increment) {
    var len = arr.length;
    if(increment > 0) {
        for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
                    var temp = arr[j];
                    arr[j] = arr[j + increment];
                    arr[j + increment] = temp;
            }
        }
        return shellSort(arr, Math.floor(increment/2));
    }
     return arr; 
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));

希尔排序-非递归实现

function shellSort(arr) {
        var len = arr.length;
        for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
                for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
                                var temp = arr[j];
                                arr[j] = arr[j + increment];
                                arr[j + increment] = temp;
                        }
                }
        }
        return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);

2.5 归并排序

2.5.1 主要思想

第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.

2.5.2 时间复杂度

平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;

2.5.3 Detaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend

2.5.4 代码实现:

归并排序-递归实现

var result = [];
function mergeArray(left, right) {
    result = [];
    while(left.length > 0 && right.length > 0) {
        if(left[0] <p>相信看了本文案例你已经掌握了方法，更多精彩请关注php中文网其它相关文章！</p><p>推荐阅读：</p><p><a href="http://www.php.cn/js-tutorial-398003.html" target="_blank">React结合TypeScript和Mobx步骤详解</a><br></p><p><a href="http://www.php.cn/js-tutorial-398045.html" target="_blank">react实现选中li高亮步骤详解</a><br></p>

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Beispiele für Sortieralgorithmen im Frontend. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!