jQuery implementiert eine rekursive unendliche Layer-Funktion

Dieses Mal bringe ich Ihnen jQuery zum Implementieren der rekursiven Unendlichkeitsebenenfunktion. Was sind die Vorsichtsmaßnahmen für jQuery, um die rekursive Unendlichkeitsebenenfunktion zu implementieren?

Chatten

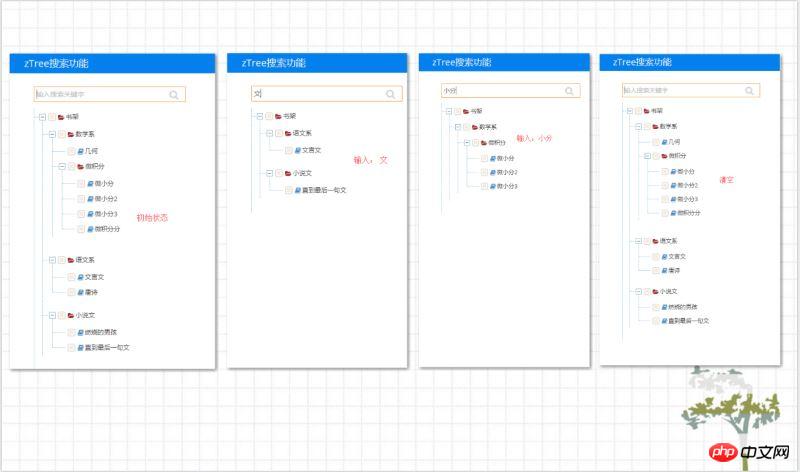
Vor zwei Tagen erzählte mir ein Freund, dass er eine Ztree-Suchfunktion wollte, und ich schlug ihm ins Gesicht: Das Gibt es zu viele Methoden, die unzählige Vorgänger nicht umgesetzt haben? Ich habe es selbst gesucht, ich war sehr beschäftigt ~ Dann hockte ich mich schweigend hin und schrieb die Suchmethode für zTree. Warum? Weil ich sagte: „Es ist unmöglich, es zu finden. Es muss viele Leute geben, die es unzählige Male gemacht haben. Wenn Sie es nicht finden können, schreibe ich es Ihnen und bitte Sie, zu Mittag zu essen.“ für eine lange Zeit und konnte es nicht finden (Tränen, mein Plan, mein Mittagessen~). Die meisten von ihnen verwenden getNodesByParamFuzzy() oder Hervorhebung in der API. Freunde sagten jedoch, dass die Anforderungen nicht erfüllt sind: 1. Wenn der Abgleich fehlschlägt, wird auch der übergeordnete Knoten ausgeblendet. 2. Die Abgleichsregeln können angepasst werden, das heißt, es können Namen und Attribute abgeglichen werden ... (Wie auch immer Ich möchte, dass es nicht scharf ist, Xiaosheng. Mit einem Lächeln im Gesicht, aber in meinem Herzen ... dann werde ich es für Sie schreiben ~), geben Sie den folgenden Text ein:

Mind Map

　

Die allgemeine Suchfunktion findet nur Schlüsselwörter innerhalb des „etablierten Bereichs (praktischer Name)“. Der „etablierte Bereich“ bedeutet, dass wir die bereits kennen Suchbereich: Zum Beispiel eine Textbibliothek, ein Dropdown-Feld, mit anderen Worten, die Größe unseres passenden Objektsatzes wurde bestimmt. Dies ist jedoch auf ztree nicht möglich. Als ich über die Implementierungslogik der Ztree-Suchfunktion nachdachte, fragte ich: Was nun, ist die Ebene dieses Baums festgelegt? Oder sind Sie nicht sicher, wie viele Schichten es gibt? Mein Bruder sah mich an und lächelte wissend: Du schreibst in unendlichen Schichten ~ Xiaoshengs Wade zuckte. . Da die Ebene des Baums ungewiss ist, ist der Suchbereich beispielsweise ungewiss. Wenn dieser Knoten ein untergeordneter Knoten ist, sollte auch der übergeordnete Knoten seines übergeordneten Knotens angezeigt werden Es wird auch angezeigt, und dann wird der übergeordnete Knoten des übergeordneten Knotens seines übergeordneten Knotens angezeigt ... Orz ... Es scheint, dass es niemals enden wird ... Es gibt keinen anderen Weg als: Rekursion, um alle übergeordneten Knoten und untergeordneten Knoten zu finden des Zielknotens.

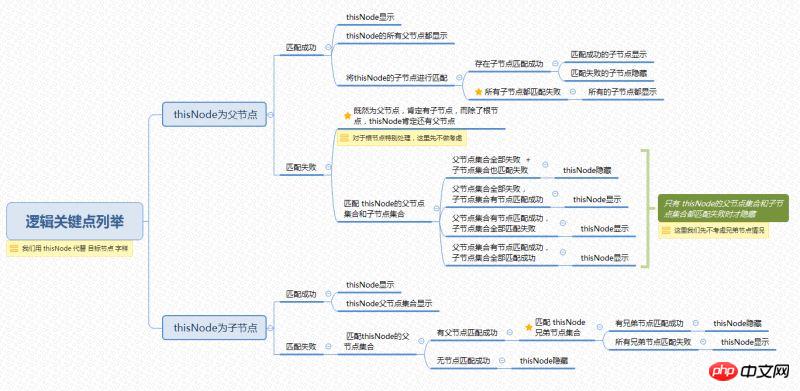
Schlüsselpunkte der Logik

In der obigen Mindmap habe ich die Logik grob aufgelistet, unter welchen Umständen der Zielknoten angezeigt wird und Was ist ein zentraler Punkt, über den wir uns im Klaren sein müssen? Schauen wir uns die Existenz des Zielknotens genauer an: Die Entwicklung der Suchfunktion ist im Kopf klar. Das einzige, was noch übrig ist, ist die Implementierungsmethode , das ist überhaupt kein Problem ~ (Xiaosheng glaubt insgeheim, dass das, was wirklich besorgniserregend ist, darin besteht, dass der Prozess der Funktion nicht klar ist. Was die Implementierungsmethode betrifft, wissen Sie alle. Richtig? 0,0 ..)

Über Baumknoten

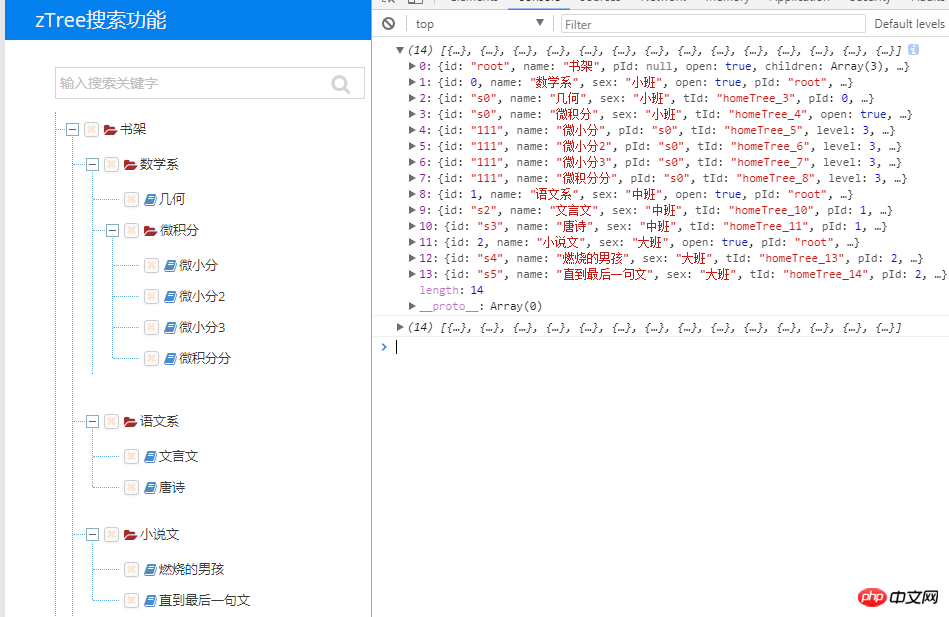
Um die verschiedenen Methoden im obigen Prozess abzuschließen, müssen wir eine Reihe von Baumknotenattributen kennen, von denen wir alle wissen, dass sie vorhanden sind Ein Artefakt wie die API ist jedoch, dass sie vollständig ist (so vollständig, dass es für uns schwierig sein kann, ein bestimmtes Attribut oder eine bestimmte Methode zu finden). Holen Sie sich schnell Für die gewünschten Attribute oder Methoden drucken wir den Baumknotensatz auf der Konsole aus: Betrachten Sie das Bild: Wir können alle Knoten sehen, einschließlich ID, Name und anderer Attribute

 var treeObj=$.fn.zTree.getZTreeObj("homeTree"); // 设置根节点
  var node = treeObj.getNodes(); // 获取根节点
  var nodes = treeObj.transformToArray(node); // 获取所有节点
  console.log(nodes);

Wenn wir uns das Bild noch einmal ansehen: Wir können verschiedene Attribute jedes Knotens sehen, einschließlich der gewünschten untergeordneten Knotensammlung, des übergeordneten Knotenattributs isParent, der Knoten-ID tId und des übergeordneten Knotens Knoten-ID parentTid.. .

Alles ist bereit, los geht's

Werfen wir einen Blick auf die relevanten Methoden. Viele kleine Details müssen entdeckt werden Während des eigentlichen Codierungsprozesses werden sie der Einfachheit halber direkt angezeigt.

Deklarieren Sie das Backup-Array:

Rufen Sie rekursiv die übergeordnete Knotensammlung des Zielknotens ab:

Rufen Sie rekursiv die untergeordnete Knotensammlung des Zielknotens ab:

// 地区搜索
 var parentArray = [];
 var childArray = [];

Es wird empfohlen, den übereinstimmenden Knotenteil zu extrahieren und eine separate Methode zu schreiben, um die Erweiterung der Übereinstimmungsregeln zu erleichtern. Hier gehen wir davon aus, dass wir zusätzlich zum Namensabgleich auch das Entity_code-Attribut des Knotens abgleichen müssen :

 // 递归获取目标节点所有父节点
 function getParentsNode(treeNode){
  var thisParentNode = treeNode.getParentNode(); //得到该节点的父节点
  if( thisParentNode != null ){ // 父节点存在
   parentArray.push(thisParentNode); // 储存至数组
   getParentsNode(thisParentNode); // 重调 
  }else{
   return false;
  }   
 }

 //匹配节点
 function matchNode(treeNode,num){
  var inputArea = $("input[name='searchArea']");
  var name = treeNode.name;
  var entityCode = treeNode.entity_code|| '';
  var val = inputArea.val(); // 获取检索值
  var numName = name.indexOf(val);
  var numCode = entityCode.indexOf(val);
  var num = -1;
  if( numName != -1 || numCode !=-1 ){
   num = 1;
  }
  if( numName == -1 && numCode == -1 ){
   num = -1; 
  }
  return num;
 }

 　　节点匹配成功方法：

 // 节点匹配成功
 function checkTrueArray(arr,treeNode){
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  for(var n=0;n<arr.length;n++){
   var thisNodeId = arr[n].tId;
   var thisNodeLi = $("#"+thisNodeId);
   thisLi.show();
   thisNodeLi.show();
  }
 }

 　　节点匹配失败方法：

 // 节点匹配失败
 function checkFalseArray(arr,treeNode){
  var result = [];
  var result2 = [];
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  var val = inputArea.val(); // 获取检索值
  var thisParent = treeNode.getParentNode(); // 获取目标节点父节点
  if( thisParent != null ){ // 有父节点
   var thisBrotherArr = treeNode.getParentNode().children; // 得到包含自身的兄弟数组
   for(var m=0;m<arr.length;m++){ // 匹配父节点
    var num = matchNode(arr[m]);
    if( num != -1 ){
     result.push(arr[m]);
    }
   }
   var resultLength = result.length;
   for( var m=0;m<thisBrotherArr.length;m++ ){ // 匹配兄弟节点
    var num = matchNode(thisBrotherArr[m]);
    if( num != -1 ){
     result2.push(thisBrotherArr[m]);
    }
   }
   var resultLength2 = result2.length;
   // 对于自身匹配失败的节点，要显示必须满足有父节点匹配成功，且兄弟级节点都匹配失败
   if( (resultLength == 0 && resultLength2 == 0) || resultLength2 != 0 ){
    thisLi.hide();
   }
   if( resultLength !=0 && resultLength2 == 0 ){
    thisLi.show();
   }
  }else{
   thisLi.hide();
  } 
 }

 　　 目标节点匹配失败 目标节点即有父节点又有子节点：

 // 目标节点匹配失败 目标节点即有父节点又有子节点
 function checkAllArray(arr,arr2,treeNode){
  var result = [];
  var result2 = [];
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  var val = inputArea.val(); // 获取检索值
  for(var m=0;m<arr.length;m++){ // 匹配子节点或父节点
   var num = matchNode(arr[m]);
   if( num != -1 ){
    result.push(arr[m]); // 匹配成功储存至数组
   }
  }
  var resultLength = result.length; // 获取匹配成功后返回的数组长度
  for(var m=0;m<arr2.length;m++){ // 匹配子节点或父节点
   var num = matchNode(arr2[m]);
   if( num != -1 ){
    result2.push(arr2[m]); // 匹配成功储存至数组
   }
  }
  var resultLength2 = result2.length; // 获取匹配成功后返回的数组长度
  if( resultLength == 0 && resultLength2 == 0 ){ // 子节点和父节点都匹配失败
   thisLi.hide();
  }else{ 
   thisLi.show(); // 有一种匹配成功或都匹配成功
  }
 }

　　定义搜索方法：

 function searchArea(treeId, treeNode){ // 定义搜索方法
  var inputArea = $("input[name='searchArea']");
  var val = inputArea.val(); // 获取检索值
  var treeObj=$.fn.zTree.getZTreeObj("homeTree"); // 设置根节点
  var node = treeObj.getNodes(); // 获取根节点
  var nodes = treeObj.transformToArray(node); // 获取所有节点
  console.log(nodes);
  for(var i=0;i
　　调用搜索方法：
 // 调用搜索方法
 $(".searchAreaBtn").click(function(treeId, treeNode){
  searchArea(treeId, treeNode);
 });
 var inputArea = $("input[name='searchArea']");
 inputArea.keyup(function(treeId, treeNode,e){
  var e = event || window.event;
  var val = inputArea.val();
  if( e.keyCode == 13 || val == "" ){
   searchArea(treeId, treeNode);
  }
 });
 　　看效果（电脑ps出问题了，用美图秀秀拼的图~囧...）：

结语
　　理论上来说应该是能支持无限层的，最多试了四层，没有问题，没有做更多测试，有兴趣的看官可以试试，需要demo的可以留言，互相学习，一起进步，么么哒~

相信看了本文案例你已经掌握了方法，更多精彩请关注php中文网其它相关文章！
推荐阅读：
jQuery与vue做出拖动验证的验证码效果

$.ajax()怎样从服务器获取json数据

jQuery动态显示select下拉列表数据
Das obige ist der detaillierte Inhalt vonjQuery implementiert eine rekursive unendliche Layer-Funktion. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!