Heim >Web-Frontend >HTML-Tutorial >Ausführliche Erklärung, wie Canvas Bezier-Kurven verwendet, um Polyliniensegmente reibungslos anzupassen
Ausführliche Erklärung, wie Canvas Bezier-Kurven verwendet, um Polyliniensegmente reibungslos anzupassen
- 小云云Original
- 2018-01-13 09:42:394182Durchsuche
In diesem Artikel werden hauptsächlich relevante Informationen zur Methode zur Verwendung der Bezier-Kurve zur reibungslosen Anpassung von Polyliniensegmenten basierend auf der Leinwand vorgestellt. Der Herausgeber findet sie recht gut, daher werde ich sie jetzt mit Ihnen teilen und als Referenz verwenden. Folgen wir dem Herausgeber und schauen wir uns das an. Ich hoffe, es kann allen helfen.
Schreiben Sie es zuerst
Dieses Mal werde ich Ihnen zeigen, wie Sie die Kanten und Ecken der gezeichneten Polyliniensegmente in der Leinwand „glätten“, also durch den Bézier-Bereich verlaufen Kurve Jeder gezeichnete Punkt ersetzt das ursprüngliche Liniendiagramm.
Warum sollten wir Polyliniensegmente reibungslos anpassen?
Werfen wir zunächst einen Blick auf den Rendereffekt des Liniendiagramms unter Echarts:
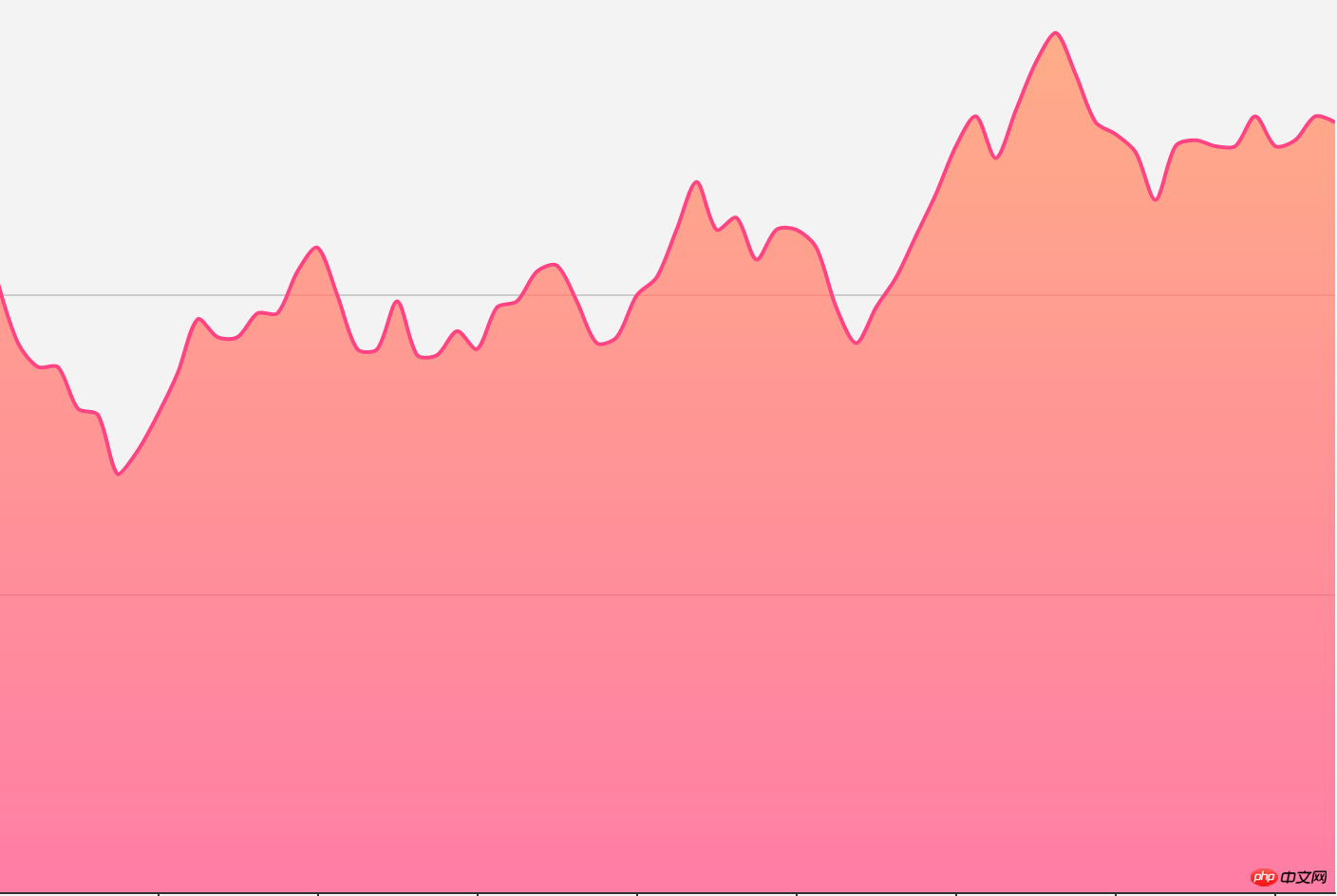
Zuerst war mir nicht aufgefallen, dass dieses Polyliniensegment tatsächlich von einer Kurve durchzogen wurde. Ich dachte nur, es sei eine einfache Punktzeichnung, also „einfach (hässlich) einfach (hässlich)“. Die Version, die ich zuerst implementiert habe, war so:
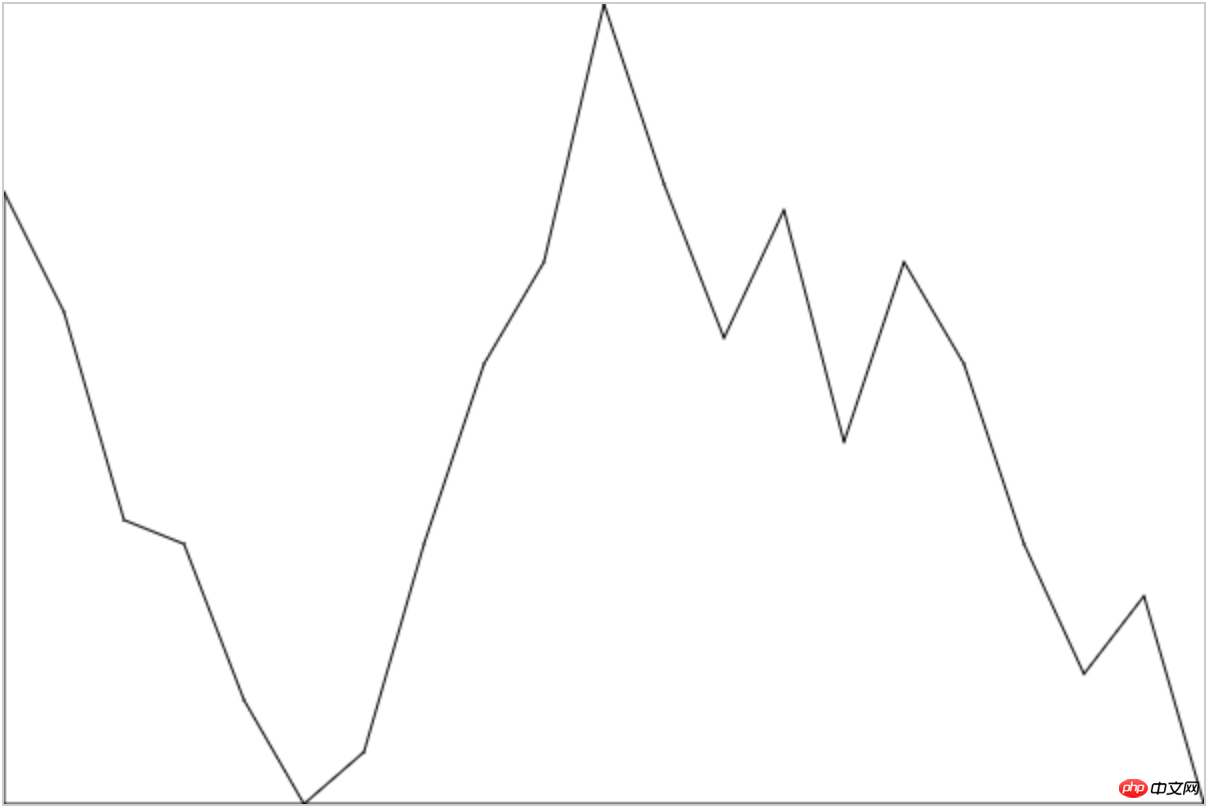
Achten Sie nicht auf den Stil. Der entscheidende Punkt ist, dass ich nach der Implementierung festgestellt habe, dass die Implementierung von Echarts so ist sehr reibungslos verlaufen, was auch spätere Diskussionen auslöste. Wie zeichnet man regelmäßig glatte Kurven?
Rendering
Werfen wir einen Blick auf die endgültige Imitationsimplementierung:
Weil ich nicht weiß, wie Echarts intern implementiert ist (Escape
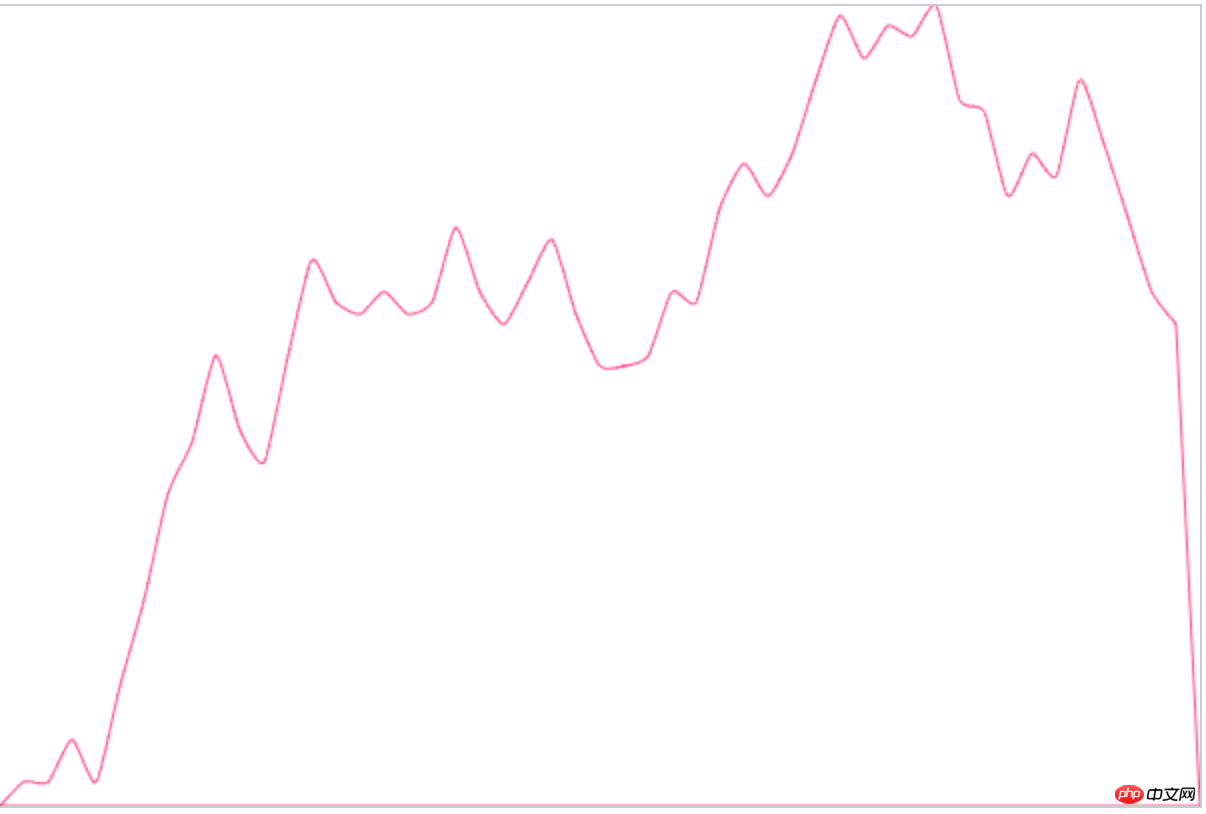
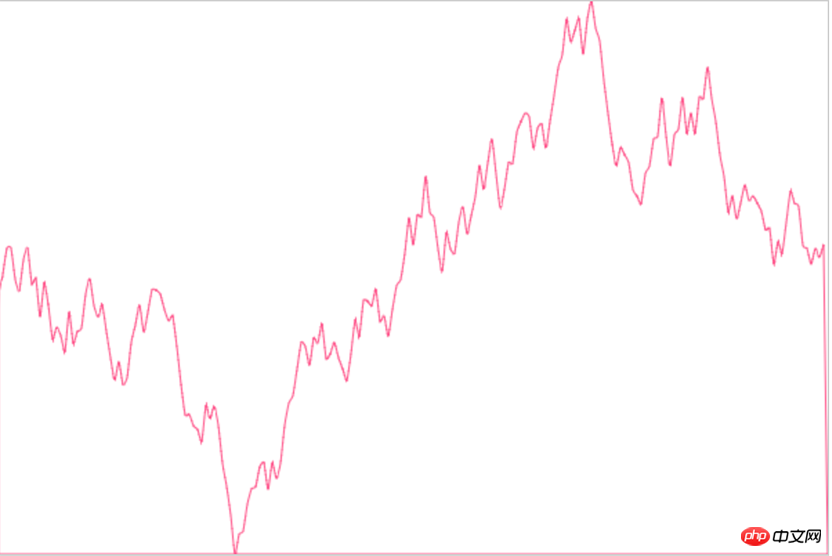
Es sieht sehr rund aus, sehr nah an unserer ursprünglichen Idee. Mal sehen, ob die Kurve durch den Zeichnungspunkt verläuft:
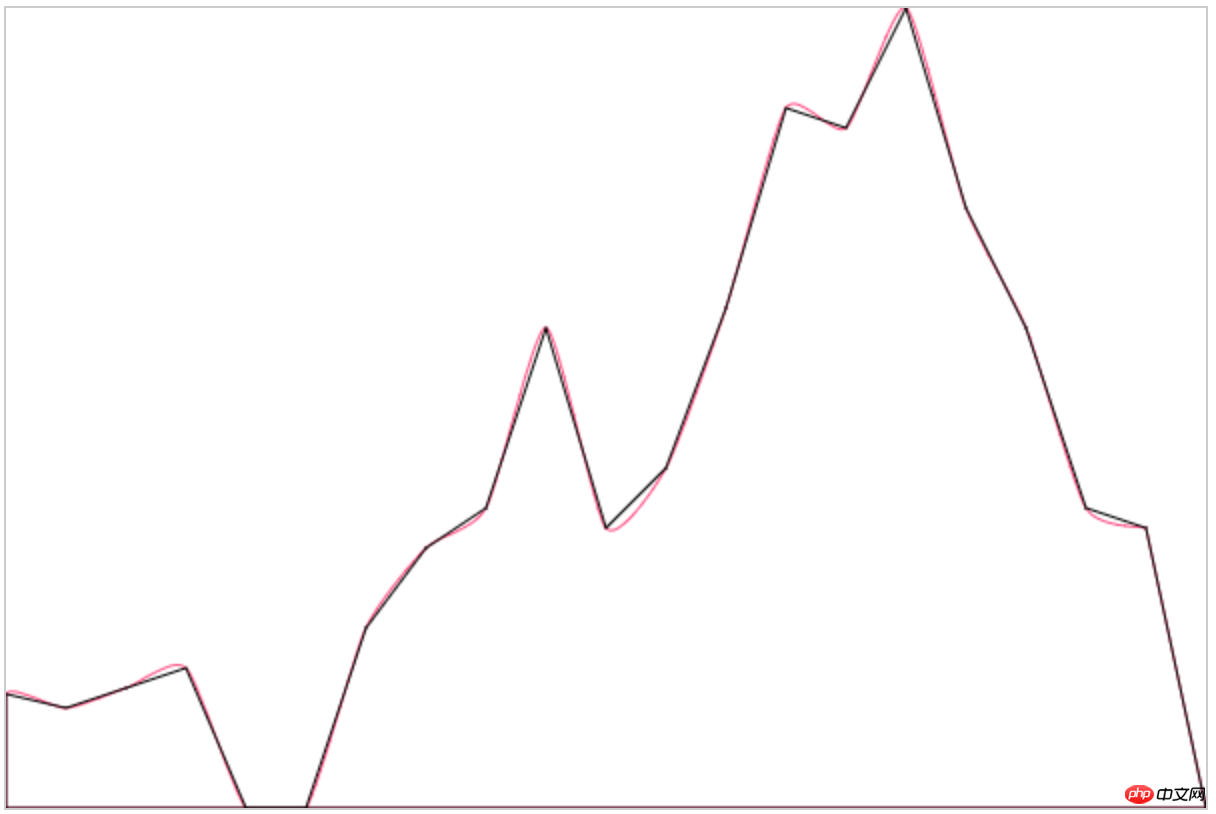
Okay! Schauen wir uns jetzt noch einmal unsere Umsetzung an
Der Umsetzungsprozess
Zeichnen Sie ein Liniendiagramm
Glatte Anpassung der Bezier-Kurve
Simulierte Daten
var data = [Math.random() * 300];
for (var i = 1; i < 50; i++) { //按照echarts
data.push(Math.round((Math.random() - 0.5) * 20 + data[i - 1]));
}
option = {
canvas:{
id: 'canvas'
},
series: {
name: '模拟数据',
itemStyle: {
color: 'rgb(255, 70, 131)'
},
areaStyle: {
color: 'rgb(255, 158, 68)'
},
data: data
}
};Zeichnen eines Liniendiagramms
Zuerst initialisieren einen Konstruktor zum Platzieren der erforderlichen Daten:
function LinearGradient(option) {
this.canvas = document.getElementById(option.canvas.id)
this.ctx = this.canvas.getContext('2d')
this.width = this.canvas.width
this.height = this.canvas.height
this.tooltip = option.tooltip
this.title = option.text
this.series = option.series //存放模拟数据
}Zeichnen Sie ein Liniendiagramm:
LinearGradient.prototype.draw1 = function() { //折线参考线
...
//要考虑到canvas中的原点是左上角,
//所以下面要做一些换算,
//diff为x,y轴被数据最大值和最小值的取值范围所平分的等份。
this.series.data.forEach(function(item, index) {
var x = diffX * index,
y = Math.floor(self.height - diffY * (item - dataMin))
self.ctx.lineTo(x, y) //绘制各个数据点
})
...
}Glätte Anpassung der Bezier-Kurve
Der Schlüsselpunkt der Bezier-Kurve ist die Auswahl von Kontrollpunkten. Auf dieser Website können verschiedene Kontrollpunkte dynamisch angezeigt werden. Der Autor entscheidet sich immer noch für Baidu. Schließlich ist er nicht gut in Mathematik :). Studierende, die sich für den jeweiligen Algorithmus interessieren, können mehr darüber erfahren. Lassen Sie uns nun über die Schlussfolgerung der Berechnung von Kontrollpunkten sprechen.
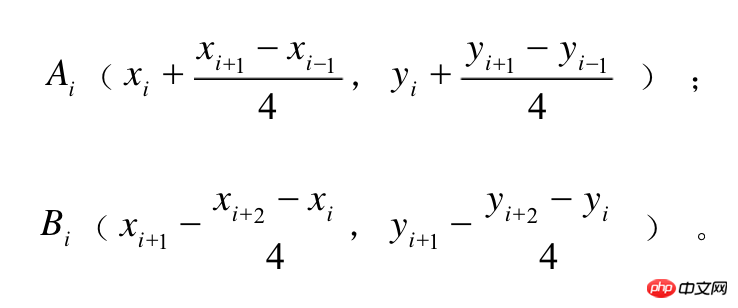
Die obige Formel umfasst vier Koordinatenpunkte, den aktuellen Punkt, den vorherigen Punkt und die nächsten beiden Punkte. Wenn der Koordinatenwert in der Abbildung unten angezeigt wird, ist dies der Fall gezeichnet Die Kurve ist wie folgt:
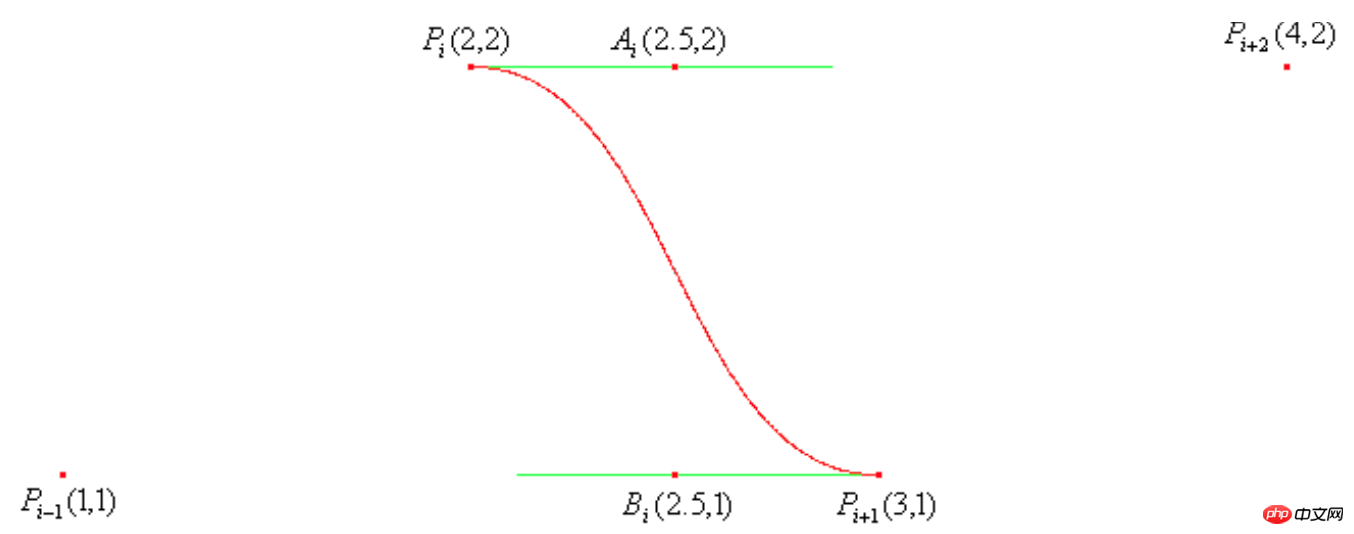
Es besteht jedoch das Problem, dass diese Formel nicht für den Startpunkt und den letzten Punkt verwendet werden kann, sondern dieser Artikel auch einen Weg angibt um mit Grenzwerten umzugehen. :

Wenn Sie also die Polylinie in eine glatte Kurve ändern, berechnen Sie die Grenzwerte und andere Kontrollpunkte und ersetzen Sie sie in der Bessel-Funktion:
//核心实现
this.series.data.forEach(function(item, index) { //找到前一个点到下一个点中间的控制点
var scale = 0.1 //分别对于ab控制点的一个正数,可以分别自行调整
var last1X = diffX * (index - 1),
last1Y = Math.floor(self.height - diffY * (self.series.data[index - 1] - dataMin)),
//前一个点坐标
last2X = diffX * (index - 2),
last2Y = Math.floor(self.height - diffY * (self.series.data[index - 2] - dataMin)),
//前两个点坐标
nowX = diffX * (index),
nowY = Math.floor(self.height - diffY * (self.series.data[index] - dataMin)),
//当期点坐标
nextX = diffX * (index + 1),
nextY = Math.floor(self.height - diffY * (self.series.data[index + 1] - dataMin)),
//下一个点坐标
cAx = last1X + (nowX - last2X) * scale,
cAy = last1Y + (nowY - last2Y) * scale,
cBx = nowX - (nextX - last1X) * scale,
cBy = nowY - (nextY - last1Y) * scale
if(index === 0) {
self.ctx.lineTo(nowX, nowY)
return
} else if(index ===1) {
cAx = last1X + (nowX - 0) * scale
cAy = last1Y + (nowY - self.height) * scale
} else if(index === self.series.data.length - 1) {
cBx = nowX - (nowX - last1X) * scale
cBy = nowY - (nowY - last1Y) * scale
}
self.ctx.bezierCurveTo(cAx, cAy, cBx, cBy, nowX, nowY);
//绘制出上一个点到当前点的贝塞尔曲线
})Da der Punkt, den ich jedes Mal überquere, der aktuelle Punkt ist, handelt es sich bei der im Artikel angegebenen Formel jedoch um einen Kontrollpunktalgorithmus, der den nächsten Punkt berechnet Der Code In der Implementierung habe ich die Berechnung aller Punkte nach vorne verschoben. Wenn Index = 0 ist, was der Anfangspunkt ist, muss keine Kurve gezeichnet werden, da wir eine Kurve vom vorherigen Punkt zum aktuellen Punkt zeichnen und es keine Kurve zu 0 gibt, die gezeichnet werden muss. Ab Index = 1 können wir normal mit dem Zeichnen der Kurve von 0 bis 1 beginnen, da es bei Index = 1 keinen zweiten Punkt davor gibt, es sich um einen Grenzwertpunkt handelt, was bedeutet, dass eine spezielle Berechnung erforderlich ist Ein Punkt. Der Rest kann nach der normalen Formel berechnet werden und die xy-Koordinaten von AB werden in die Bessel-Funktion eingesetzt.
Verwandte Empfehlungen:
Canvas implementiert Bezier-Kurven höherer Ordnung
Verwenden Sie CSS, um Bezier-Kurven zu erstellen
Detaillierte Erläuterung der Anwendung der Bezier-Kurve
Das obige ist der detaillierte Inhalt vonAusführliche Erklärung, wie Canvas Bezier-Kurven verwendet, um Polyliniensegmente reibungslos anzupassen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

