Heim >Web-Frontend >HTML-Tutorial >Canvas implementiert eine Bezier-Kurve höherer Ordnung
Canvas implementiert eine Bezier-Kurve höherer Ordnung
- 小云云Original
- 2018-01-13 09:40:132906Durchsuche
In diesem Artikel wird hauptsächlich die Implementierung einer Bezier-Kurve höherer Ordnung (Bezier-Kurvengenerator N-Ordnung) in Canvas vorgestellt. Jetzt werde ich sie mit Ihnen teilen und als Referenz verwenden. Folgen wir dem Herausgeber und schauen wir uns das an. Ich hoffe, es kann allen helfen.
Zuerst schreiben
Da der native Canvas nur Bezier-Kurven bis zur dritten Ordnung unterstützt, was soll ich tun, wenn ich mehrere Kontrollpunkte hinzufügen möchte? (Selbst die komplexesten Kurven können mit Bezier dritter Ordnung simuliert werden.) Gleichzeitig ist es für uns schwierig, die Position der Bezier-Kontrollpunkte sehr intuitiv klar zu verstehen und wie stark die Kontrollpunkte eingestellt werden sollten, um die Kurve zu bilden, die wir haben wollen. . Um die beiden oben genannten Probleme zu lösen, scheint es in der Community keine N-Level-Lösung (js-Version) zu geben. Daher nimmt der Autor dieses Mal Open Source bezierMaker.js sehr ernst!
bezierMaker.js unterstützt theoretisch die Generierung von Bezier-Kurven N-ter Ordnung und bietet Entwicklern auch ein Testgelände zum Hinzufügen und Ziehen von Kontrollpunkten, um letztendlich eine Reihe von Zeichenanimationen zu generieren. Für Entwickler ist es sehr intuitiv, die verschiedenen Erzeugungskurven zu kennen, die Kontrollpunkten an verschiedenen Positionen entsprechen.
Wenn Ihnen diese Arbeit gefällt, willkommen bei Star, schließlich sind Sterne hart verdient. .
Projektadresse: hier✨✨✨
Warum wird eine Teststelle benötigt?
Beim Zeichnen komplexer Bezier-Kurven höherer Ordnung können Sie die genaue Position der Kontrollpunkte der benötigten Kurve nicht kennen. Durch Simulation im Testfeld können die Koordinatenwerte der Kontrollpunkte in Echtzeit ermittelt werden. Die erhaltenen Punktkoordinaten werden in ein Objektarray umgewandelt und an die BezierMaker-Klasse übergeben, um die Zielkurve zu generieren
Rendern


Funktion
[x] Dem Teststandort können beliebig viele Kontrollpunkte hinzugefügt werden
[x] Der Teststandort unterstützt die Anzeige der Formationsanimation der Kurvenzeichnung
[x] Die Kontrollpunkte können frei verschoben werden
[x] Unterstützt die Anzeige von Tangentenlinien im Entstehungsprozess von Bezier-Kurven
-
[ x] Das Zeichnen von Bezier-Kurven der Ordnung 3 und darunter verwendet eine native API
Wir stellen vor:
<script src="./bezierMaker.js"></script>
Zeichnen Sie
den obigen Effekt. Das Bild zeigt die Verwendung der Teststelle. Nachdem Sie die genauen Koordinaten der Kontrollpunkte über die Teststelle erhalten haben, können Sie bezierMaker.js aufrufen Zeichnen Sie die Kurve direkt.
/**
* canvas canvas的dom对象
* bezierCtrlNodesArr 控制点数组,包含x,y坐标
* color 曲线颜色
*/
var canvas = document.getElementById('canvas')
//3阶之前采用原生方法实现
var arr0 = [{x:70,y:25},{x:24,y:51}]
var arr1 = [{x:233,y:225},{x:170,y:279},{x:240,y:51}]
var arr2 = [{x:23,y:225},{x:70,y:79},{x:40,y:51},{x:300, y:44}]
var arr3 = [{x:333,y:15},{x:70,y:79},{x:40,y:551},{x:170,y:279},{x:17,y:239}]
var arr4 = [{x:53,y:85},{x:170,y:279},{x:240,y:551},{x:70,y:79},{x:40,y:551},{x:170,y:279}]
var bezier0 = new BezierMaker(canvas, arr0, 'black')
var bezier1 = new BezierMaker(canvas, arr1, 'red')
var bezier2 = new BezierMaker(canvas, arr2, 'blue')
var bezier3 = new BezierMaker(canvas, arr3, 'yellow')
var bezier4 = new BezierMaker(canvas, arr4, 'green')
bezier0.drawBezier()
bezier1.drawBezier()
bezier2.drawBezier()
bezier3.drawBezier()
bezier4.drawBezier()Zeichnungsergebnis

Wenn weniger als 3 Kontrollpunkte vorhanden sind, werden die nativen verwendet . API-Schnittstelle. Wenn mehr als zwei Kontrollpunkte vorhanden sind, verwenden wir die von uns implementierte Funktion zum Zeichnen der Punkte.
Grundprinzipien
Zeichnen von Bezier-Kurven
Der Kernpunkt beim Zeichnen von Bezier-Kurven liegt in der Anwendung der Bezier-Formel:
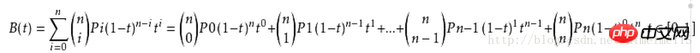
P0-Pn in dieser Formel stellt die verschiedenen Leistungsoperationen jedes Punktes und das Verhältnis t vom Startpunkt zu jedem Kontrollpunkt und dann zum Endpunkt dar.
BezierMaker.prototype.bezier = function(t) { //贝塞尔公式调用
var x = 0,
y = 0,
bezierCtrlNodesArr = this.bezierCtrlNodesArr,
//控制点数组
n = bezierCtrlNodesArr.length - 1,
self = this
bezierCtrlNodesArr.forEach(function(item, index) {
if(!index) {
x += item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
} else {
//factorial为阶乘函数
x += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
}
})
return {
x: x,
y: y
}
}Durchqueren Sie alle Punkte und berechnen Sie die aktuelle Position auf der Bezier-Kurve basierend auf dem Wert des aktuellen Anteils t (0<=t<=1) Der Punkt Koordinaten x, y. Der Autor teilt den Wert von t in 1000 Teile, d. h. t+=0,01 für jede Operation. Die zu diesem Zeitpunkt berechneten x- und y-Werte sind die Punkte, nachdem die Bezier-Kurve in 1000 Teile geteilt wurde. Wenn der t-Wert 1000 Mal von 0 auf 1 durchlaufen wird, werden 1000 x- und y-entsprechende Koordinaten generiert, und eine Bezier-Kurve höherer Ordnung kann durch aufeinanderfolgendes Zeichnen von Punkten und Linien simuliert werden.
Die Ableitung der Bezier-Formel wird der Autor in einem späteren Artikel konkret erläutern. Jetzt müssen Sie nur noch wissen, dass wir die Bezier-Formel verwenden, um die Punkte zu berechnen, an denen die tatsächliche Bezier-Kurve in 1000 gleiche Teile geteilt wird . Eine Klassenkurve kann simuliert werden, indem jeder Punkt mit einer Geraden verbunden wird.
Für die Implementierung der Simulationsfeld-Bezier-Kurvengenerierungsanimation
Auf diesen Teil des relevanten Codes kann hier verwiesen werden
Die Gesamtidee besteht darin, jede Ebene mithilfe von Rekursion zu steuern Die Punkte werden als Bessel-Funktionen erster Ordnung behandelt, um die nächste Ebene von Kontrollpunkten und entsprechenden Verbindungen zu berechnen. Der Autor wird die spezifische Logik bis zur ausführlichen Erläuterung der Prinzipien der Bezier-Kurvenformel belassen, um die Animationserzeugungsprinzipien der Testseite zu klären~
Verwandte Empfehlungen:
Verwenden Sie CSS, um eine Bezier-Kurve zu erstellen
Detaillierte Erläuterung der Anwendung der Bezier-Kurve
Codedemonstration zur Implementierung des Canvas-Bezier-Kurveneffekts
Das obige ist der detaillierte Inhalt vonCanvas implementiert eine Bezier-Kurve höherer Ordnung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

