Zusammenfassung von acht in Python implementierten Sortieralgorithmen (Teil 1)

Dieser Artikel stellt hauptsächlich den ersten der acht in Python implementierten Sortieralgorithmen im Detail vor. Interessierte Freunde können sich auf

Sortieren

beziehen Sortieren ist eine Operation, die häufig in Computern durchgeführt wird. Ihr Zweck besteht darin, eine Reihe „ungeordneter“ Datensatzsequenzen in eine „geordnete“ Datensatzsequenz umzuwandeln. Unterteilt in interne Sortierung und externe Sortierung. Wenn der gesamte Sortiervorgang ohne Zugriff auf den externen Speicher abgeschlossen werden kann, wird diese Art von Sortierproblem als interne Sortierung bezeichnet. Wenn dagegen die Anzahl der an der Sortierung beteiligten Datensätze groß ist und der Sortiervorgang der gesamten Sequenz nicht vollständig im Speicher abgeschlossen werden kann und Zugriff auf den externen Speicher erforderlich ist, wird diese Art von Sortierproblem als externe Sortierung bezeichnet. Der Prozess der internen Sortierung ist ein Prozess, bei dem die Länge der geordneten Datensatzfolge schrittweise erweitert wird.

Sehen Sie sich die Bilder an, um Ihr Verständnis zu verdeutlichen:

Gehen Sie davon aus, dass es in der zu sortierenden Datensatzreihenfolge mehrere Datensätze mit demselben Schlüsselwort gibt Nach dem Sortieren bleibt die relative Reihenfolge dieser Datensätze unverändert, das heißt, in der ursprünglichen Reihenfolge ist ri = rj und ri steht vor rj, und in der sortierten Reihenfolge steht ri immer noch vor rj, dann heißt dieser Sortieralgorithmus stabil. Andernfalls heißt es instabil.

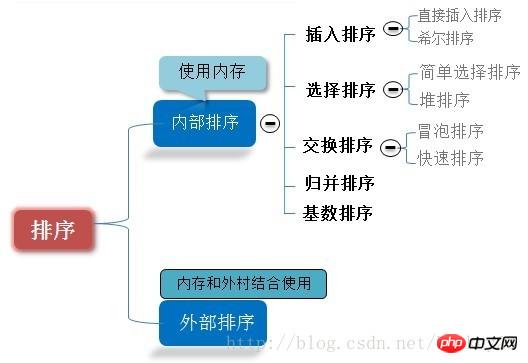
Gemeinsame Sortieralgorithmen

Schnellsortierung, Hill-Sortierung, Heap-Sortierung und Direktauswahlsortierung sind keine stabilen Sortieralgorithmen, während Radix-Sortierung, Blasensortierung und Direkteinfügung keine stabilen Sortieralgorithmen sind Sortieren, Halbeinfügungssortierung und Zusammenführungssortierung sind stabile Sortieralgorithmen

In diesem Artikel wird Python verwendet, um Blasensortierung, Einfügungssortierung, Hill-Sortierung, Schnellsortierung, Direktauswahlsortierung, Heap-Sortierung, Zusammenführungssortierung und Radix zu implementieren sort. Diese acht Sortieralgorithmen.

1. Blasensortierung

Algorithmusprinzip:

Ein Satz ungeordneter Daten a[1], a[ ist bekannt 2],.. .a[n], sie müssen in aufsteigender Reihenfolge sortiert werden. Vergleichen Sie zunächst die Werte von a[1] und a[2]. Wenn a[1] größer als a[2] ist, tauschen Sie die Werte der beiden aus, andernfalls bleiben sie unverändert. Vergleichen Sie dann die Werte von a[2] und a[3]. Wenn a[2] größer als a[3] ist, tauschen Sie die Werte der beiden aus, andernfalls bleiben sie unverändert. Vergleichen Sie dann a [3] und a [4] usw. und vergleichen Sie schließlich die Werte von a [n-1] und a [n]. Nach einer Verarbeitungsrunde muss der Wert von a[n] der größte in diesem Datensatz sein. Wenn a[1]~a[n-1] erneut auf die gleiche Weise verarbeitet wird, muss der Wert von a[n-1] der größte unter a[1]~a[n-1] sein. Verarbeiten Sie dann a[1]~a[n-2] eine Runde lang auf die gleiche Weise und so weiter. Nach insgesamt n-1 Verarbeitungsrunden werden a[1], a[2],...a[n] in aufsteigender Reihenfolge angeordnet. Die absteigende Sortierung ähnelt der aufsteigenden Sortierung. Wenn a[1] kleiner als a[2] ist, werden die Werte der beiden ausgetauscht, andernfalls bleiben sie unverändert und so weiter. Im Allgemeinen wird nach jeder Sortierrunde die größte (oder kleinste) Zahl an das Ende der Datensequenz verschoben, und theoretisch werden insgesamt n(n-1)/2 Austausche durchgeführt.

Vorteile: Stabil;
Nachteile: Langsam, es können nur zwei benachbarte Daten gleichzeitig verschoben werden.

Python-Code-Implementierung:

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
 lstlen = len(lst1);i = 0
 while i < lstlen:
  for j in range(1,lstlen):
   if lst1[j-1] > lst1[j]:
   #对比相邻两个元素的大小，小的元素上浮
    lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
  i += 1
  print &#39;sorted{}: {}&#39;.format(i, lst1)
 print &#39;-------------------------------&#39;
 return lst1
bubble_sort_basic(lst1)

Verbesserung des Blasensortierungsalgorithmus

Für Sequenzen, die völlig ungeordnet sind oder keine sich wiederholenden Elemente haben, gibt es für den oben genannten Algorithmus keinen Raum für Verbesserungen, die auf derselben Idee basieren. Wenn jedoch sich wiederholende Elemente in einer Sequenz vorhanden sind oder einige Elemente in der richtigen Reihenfolge sind, wird diese Situation zwangsläufig vorliegen. Bei unnötiger wiederholter Sortierung können wir dem Sortiervorgang eine symbolische Variablenänderung hinzufügen, um zu markieren, ob während eines bestimmten Sortiervorgangs ein Datenaustausch stattfindet. Wenn während eines bestimmten Sortiervorgangs kein Datenaustausch stattfindet, bedeutet dies, dass die Daten bereits wie erforderlich angeordnet sind , die Sortierung kann sofort beendet werden, um unnötigen Vergleichsprozess zu vermeiden. Der verbesserte Beispielcode lautet wie folgt:

lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
 lstlen = len(lst2)
 i = 1;times = 0
 while i > 0:
  times += 1
  change = 0
  for j in range(1,lstlen):
   if lst2[j-1] > lst2[j]:
   #使用标记记录本轮排序中是否有数据交换
    change = j
    lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
  print 'sorted{}: {}'.format(times,lst2)
  #将数据交换标记作为循环条件，决定是否继续进行排序
  i = change
 return lst2
bubble_sort_improve(lst2)

Die laufenden Screenshots in den beiden Fällen lauten wie folgt:

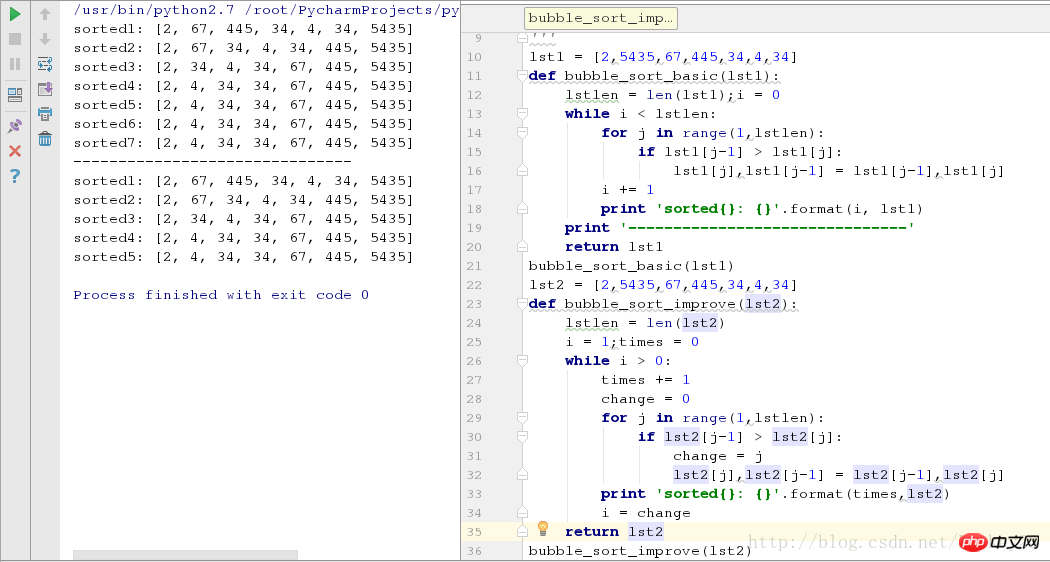
Wie aus der obigen Abbildung ersichtlich ist, reduziert der optimierte Algorithmus für Sequenzen, in denen einige Elemente der Reihe nach angeordnet sind, zwei Sortierrunden.

2. Auswahlsortierung

Algorithmusprinzip:

Wählen Sie das kleinste (oder größte) Element am Ende des sortierten Arrays aus, bis alle die zu sortierenden Datenelemente sind erschöpft.
Die Direktauswahlsortierung von Dateien mit n Datensätzen kann n-1 Mal die Direktauswahlsortierung durchlaufen, um geordnete Ergebnisse zu erhalten:

①Anfangszustand: Der ungeordnete Bereich ist R[1..n], geordnet The Bereich ist leer.
②Die erste Sortierung
Wählen Sie den Datensatz R[k] mit dem kleinsten Schlüsselwort im ungeordneten Bereich R[1..n] aus und kombinieren Sie ihn mit dem ersten Datensatz R[1] im ungeordneten Bereich Exchange, also dass R[1..1] und R[2..n] ein neuer geordneter Bereich mit einer um 1 erhöhten Anzahl von Datensätzen und ein neuer ungeordneter Bereich mit einer um 1 verringerten Anzahl von Datensätzen werden.
......
③Die i-te Sortierung
Wenn die i-te Sortierung beginnt, sind der aktuelle geordnete Bereich und der ungeordnete Bereich R[1..i-1] und R(1≤ i≤n bzw. -1). Diese Sortieroperation wählt den Datensatz R[k] mit dem kleinsten Schlüssel aus dem aktuellen ungeordneten Bereich aus und tauscht ihn mit dem ersten Datensatz R im ungeordneten Bereich aus, sodass R[1..i] bzw. R zu Datensatznummern werden Die Anzahl der neu geordneten Bereiche erhöht sich um 1 und die Anzahl der Datensätze verringert sich um 1. Der neue ungeordnete Bereich.
Auf diese Weise kann die Direktauswahlsortierung von Dateien mit n Datensätzen durch n-1 Direktauswahlsortierdurchgänge geordnete Ergebnisse erzielen.

优点：移动数据的次数已知（n-1次）；
缺点：比较次数多，不稳定。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
 lstlen = len(lst)
 for i in range(0,lstlen):
  min = i
  for j in range(i+1,lstlen):
  #从 i+1开始循环遍历寻找最小的索引
   if lst[min] > lst[j]:
    min = j
  lst[min],lst[i] = lst[i],lst[min]
  #一层遍历结束后将最小值赋给外层索引i所指的位置，将i的值赋给最小值索引  
  print('The {} sorted: {}'.format(i+1,lst))
 return lst
sorted = selection_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

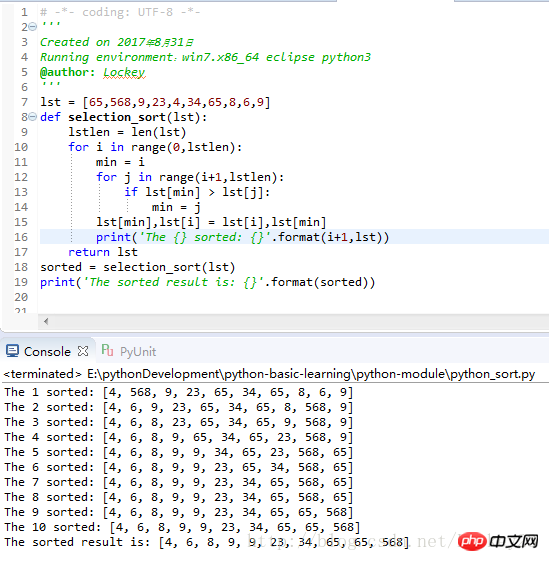
3. 插入排序

算法原理：

已知一组升序排列数据a[1]、a[2]、……a[n]，一组无序数据b[1]、b[2]、……b[m]，需将二者合并成一个升序数列。首先比较b[1]与a[1]的值，若b[1]大于a[1]，则跳过，比较b[1]与a[2]的值，若b[1]仍然大于a[2]，则继续跳过，直到b[1]小于a数组中某一数据a[x]，则将a[x]~a[n]分别向后移动一位，将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。（若无数组a，可将b[1]当作n=1的数组a）
优点：稳定，快；
缺点：比较次数不一定，比较次数越多，插入点后的数据移动越多，特别是当数据总量庞大的时候，但用链表可以解决这个问题。

算法复杂度

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
 count = len(lst)
 for i in range(1, count):
  key = lst[i]
  j = i - 1
  while j >= 0:
   if lst[j] > key:
    lst[j + 1] = lst[j]
    lst[j] = key
   j -= 1
  print('The {} sorted: {}'.format(i,lst))
 return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

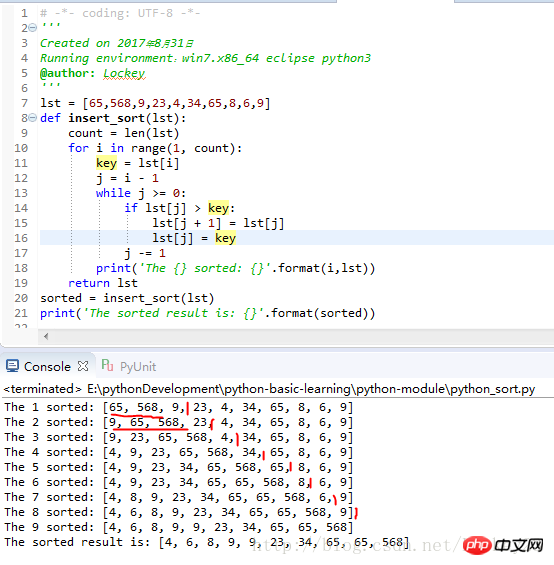
由排序过程可知，每次往已经排好序的序列中插入一个元素，然后排序，下次再插入一个元素排序。。。直到所有元素都插入，排序结束

4. 希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

算法原理

算法核心为分组（按步长）、组内插入排序

已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。发现当n不大时，插入排序的效果很好。首先取一增量d(d

python代码实现：

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
 print 'orginal list is {}'.format(lst)
 count = len(lists)
 step = 2
 times = 0
 group = int(count/step)
 while group > 0:
  for i in range(0, group):
   times += 1
   j = i + group
   while j < count:
    k = j - group
    key = lists[j]
    while k >= 0:
     if lists[k] > key:
      lists[k + group] = lists[k]
      lists[k] = key
     k -= group
    j += group
    print &#39;The {} sorted: {}&#39;.format(times,lists)
  group = int(group/step)
 print &#39;The final result is: {}&#39;.format(lists)
 return lists
shell_sort(lst)

运行测试结果截图：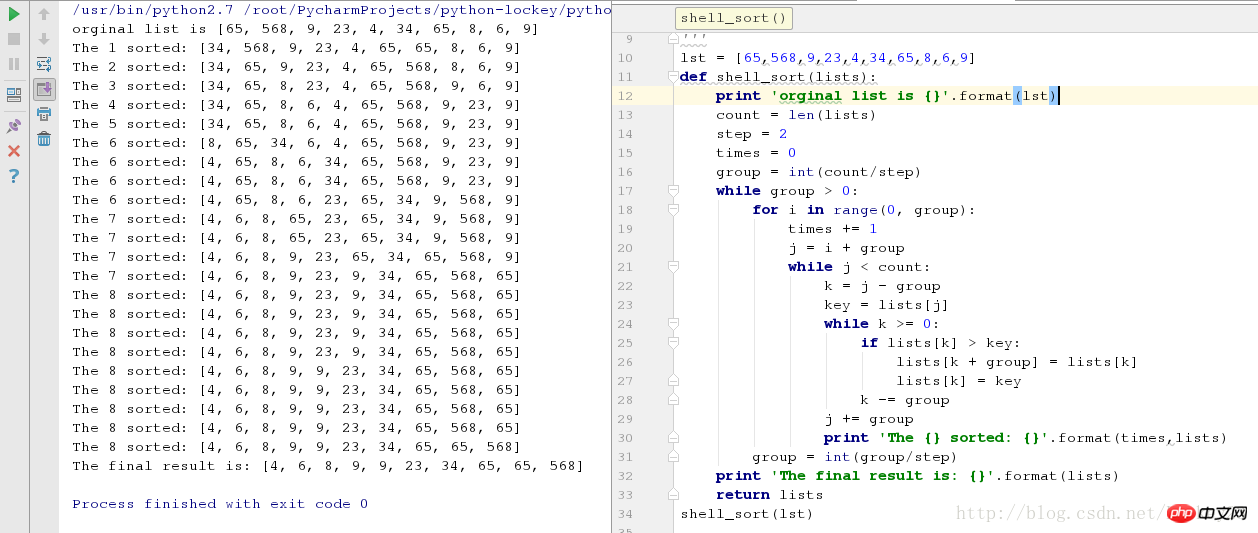

过程分析：

第一步：

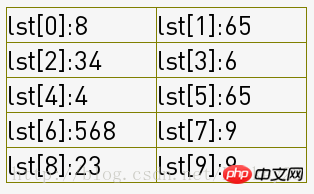
1-5：将序列分成了5组（group = int(count/step)）,如下图，一列为一组：

然后各组内进行插入排序，经过5（5组*1次）次组内插入排序得到了序列：

The 1-5 sorted：[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步：

6666-7777：将序列分成了2组（group = int(group/step)）,如下图，一列为一组：

 

然后各组内进行插入排序，经过8（2组*4次）次组内插入排序得到了序列：

The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步：

888888888：对上一个排序结果得到的完整序列进行插入排序：

[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

经过9（1组*10 -1）次插入排序后：

The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]

Hill-Sorting-Aktualitätsanalyse ist schwierig. Die Anzahl der Schlüsselcodevergleiche und die Anzahl der aufgezeichneten Züge hängen von der Auswahl der inkrementellen Faktorsequenz ab. Unter bestimmten Umständen kann die Anzahl der Schlüsselcodevergleiche und die Anzahl der aufgezeichneten Züge variieren genau geschätzt. Bisher hat noch niemand eine Methode zur Auswahl der besten inkrementellen Faktorfolge angegeben. Die Reihenfolge der inkrementellen Faktoren kann auf verschiedene Arten verwendet werden, einschließlich ungerader Zahlen und Primzahlen. Es ist jedoch zu beachten, dass es außer 1 keine gemeinsamen Faktoren zwischen den inkrementellen Faktoren gibt und der letzte inkrementelle Faktor 1 sein muss. Die Hill-Sortiermethode ist eine instabile Sortiermethode

Das obige ist der detaillierte Inhalt vonZusammenfassung von acht in Python implementierten Sortieralgorithmen (Teil 1). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!