Detaillierte Erläuterung des Grafikcodes des klassischen C#-Sortieralgorithmus (Teil 2)

Dieser Artikel stellt hauptsächlich den nächsten Teil der Serie von sieben klassischen Sortieralgorithmen von C# vor, der direkten Einfügungssortierung, der Hill-Sortierung und der Zusammenführungssortierung. Interessierte Freunde können sich auf

Heute werde ich mit Ihnen über die letzten drei Sortierungen sprechen: Direkteinfügungssortierung, Hügelsortierung und Zusammenführungssortierung.

Direkteinfügungssortierung:

Diese Art der Sortierung ist eigentlich ganz einfach zu verstehen, wenn wir eine zufällige Kartenhand fangen. Wir müssen die Pokerkarten nach Größe sortieren. Nach 30 Sekunden sind die Pokerkarten aussortiert, 4 3er, 5 s, wow ... Erinnern Sie sich, wie wir es damals sortiert haben.

Die Karte ganz links ist 3, die zweite Karte ist wieder 3. Beeilen Sie sich und stecken Sie sie hinter die erste Karte Beeil dich. Lege sie nach der zweiten Karte ein, und die fünfte Karte ist wieder 3, ich bin begeistert, haha, eine Kanone ist geboren.

Wie wäre es damit? Algorithmen sind überall im Leben und bereits in unser Leben und Blut integriert.

Das Folgende ist eine Erklärung des obigen Bildes: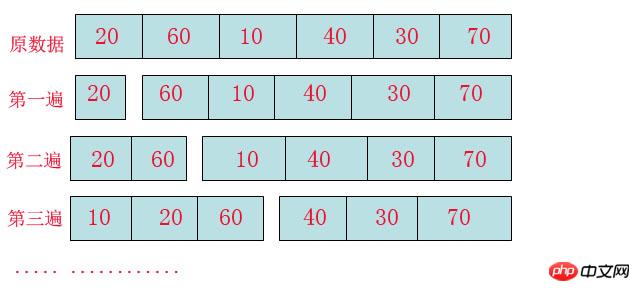

Wenn ich mir dieses Bild ansehe, weiß ich nicht, ob Sie es beim Einfügen verstehen können ,

Array Es wird in zwei Typen unterteilt: „geordneter Array-Block“ und „ungeordneter Array-Block“. Ja, im ersten Durchgang wird eine Zahl 20 als geordneter Typ aus dem „ungeordneten Array-Block“ extrahiert Array-Block.

Im zweiten Durchgang wird eine Zahl 60 aus dem „ungeordneten Array-Block“ extrahiert und geordnet in den „geordneten Array-Block“ eingefügt, also 20, 60.

Dasselbe gilt für den dritten Durchgang, aber der Unterschied besteht darin, dass 10 kleiner als der Wert des geordneten Arrays ist, sodass die Positionen von 20 und 60 nach hinten verschoben werden, um eine Position für 10 freizugeben einzufügen.

Dann können alle Einfügungen nach dieser Regel abgeschlossen werden.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace InsertSort
{
 public class Program
 {
  static void Main(string[] args)
  {
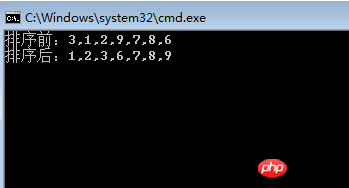
   List<int> list = new List<int>() { 3, 1, 2, 9, 7, 8, 6 };

   Console.WriteLine("排序前：" + string.Join(",", list));

   InsertSort(list);

   Console.WriteLine("排序后：" + string.Join(",", list));
  }

  static void InsertSort(List<int> list)
  {
   //无须序列
   for (int i = 1; i < list.Count; i++)
   {
    var temp = list[i];

    int j;

    //有序序列
    for (j = i - 1; j >= 0 && temp < list[j]; j--)
    {
     list[j + 1] = list[j];
    }
    list[j + 1] = temp;
   }
  }
 }
}

Hügelsortierung:

Beachten Sie die „Einfügungssortierung“: Tatsächlich Es ist nicht schwer festzustellen, dass sie einen Mangel hat:

Wenn die Daten „

5, 4, 3, 2, 1“ lauten, werden wir zu diesem Zeitpunkt einen Datensatz erstellen Beim Einfügen in einen „geordneten Block“ wird geschätzt, dass wir abstürzen und die Position bei jedem Einfügen verschoben wird. Zu diesem Zeitpunkt kann man sich die Effizienz der Einfügungssortierung vorstellen.

Die Shell hat den Algorithmus basierend auf dieser Schwäche verbessert und eine Idee namens „

Schrumpfende inkrementelle Sortiermethode“ integriert. Es ist eigentlich ganz einfach, aber etwas zu beachten ist:

Inkremente sind nicht zufällig, sondern folgen einem Muster.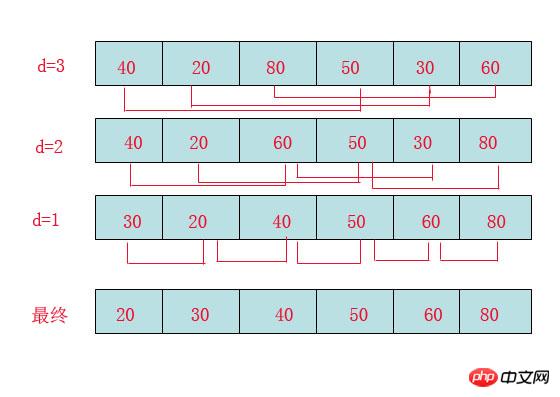

Zuerst müssen wir die Methode der Inkrementierung klären:

Die Methode zur Ermittlung des ersten Inkrements ist: d=count/2;

Die Methode zum Ermitteln des zweiten Inkrements lautet: d=(count/2)/2;

Schließlich bis: d=1;

Sehen Sie sich das beobachtete Phänomen an Bild oben:

Wenn d=3: Vergleiche 40 mit 50. Da 50 größer ist, gibt es keinen Austausch.

Wenn man 20 mit 30 vergleicht, weil 30 größer ist, gibt es keinen Umtausch.

Vergleichen Sie 80 mit 60. Da 60 kleiner ist, tauschen Sie sie aus.

Wenn d = 2: Vergleichen Sie 40 mit 60, tauschen Sie nicht aus und tauschen Sie 60 mit 30 aus. Zu diesem Zeitpunkt sind die ausgetauschten 30 kleiner als die vorherigen 40, und 40 und 30 müssen ausgetauscht werden im Bild oben dargestellt.

Vergleichen Sie 20 mit 50 ohne Umtausch, vergleichen Sie weiterhin 50 mit 80 ohne Umtausch.

Wenn d=1: Dies ist die zuvor erwähnte Einfügungssortierung, aber die Reihenfolge ist zu diesem Zeitpunkt fast in Ordnung, sodass die Einfügungssortierung eine große Leistungsverbesserung aufweist.

Da „Hill Sort“ eine verbesserte Version von „Insertion Sort“ ist, müssen wir dann vergleichen, wie viel schneller es unter 10.000 Zahlen sein kann?

Machen wir einen Test:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace ShellSort
{
 public class Program
 {
  static void Main(string[] args)
  {
   //5次比较
   for (int i = 1; i <= 5; i++)
   {
    List<int> list = new List<int>();

    //插入1w个随机数到数组中
    for (int j = 0; j < 10000; j++)
    {
     Thread.Sleep(1);
     list.Add(new Random((int)DateTime.Now.Ticks).Next(10000, 1000000));
    }

    List<int> list2 = new List<int>();
    list2.AddRange(list);

    Console.WriteLine("\n第" + i + "次比较：");

    Stopwatch watch = new Stopwatch();

    watch.Start();
    InsertSort(list);
    watch.Stop();

    Console.WriteLine("\n插入排序耗费的时间：" + watch.ElapsedMilliseconds);
    Console.WriteLine("输出前十个数:" + string.Join(",", list.Take(10).ToList()));

    watch.Restart();
    ShellSort(list2);
    watch.Stop();

    Console.WriteLine("\n希尔排序耗费的时间：" + watch.ElapsedMilliseconds);
    Console.WriteLine("输出前十个数:" + string.Join(",", list2.Take(10).ToList()));

   }
  }

  ///<summary>
/// 希尔排序
///</summary>
///<param name="list"></param>
  static void ShellSort(List<int> list)
  {
   //取增量
   int step = list.Count / 2;

   while (step >= 1)
   {
    //无须序列
    for (int i = step; i < list.Count; i++)
    {
     var temp = list[i];

     int j;

     //有序序列
     for (j = i - step; j >= 0 && temp < list[j]; j = j - step)
     {
      list[j + step] = list[j];
     }
     list[j + step] = temp;
    }
    step = step / 2;
   }
  }

  ///<summary>
/// 插入排序
///</summary>
///<param name="list"></param>
  static void InsertSort(List<int> list)
  {
   //无须序列
   for (int i = 1; i < list.Count; i++)
   {
    var temp = list[i];

    int j;

    //有序序列
    for (j = i - 1; j >= 0 && temp < list[j]; j--)
    {
     list[j + 1] = list[j];
    }
    list[j + 1] = temp;
   }
  }
 }
}

Der Screenshot sieht wie folgt aus:

Wie Sie sehen, wurde die Hill-Sortierung stark optimiert. Bei der W-Level-Sortierung beträgt der Unterschied mehr als das 70-fache.

Sortierung zusammenführen:

Persönlich ist die Sortierung, die wir leicht verstehen können, grundsätzlich O (n^2), und die Sortierung, die schwieriger zu verstehen ist, ist im Grunde O (n^2). Es ist N(LogN), daher ist die Zusammenführungssortierung auch relativ schwer zu verstehen, insbesondere wenn es um das Schreiben des Codes geht

Ich habe einen ganzen Nachmittag gebraucht, um es herauszufinden. hehe.

Erster Blick auf das Bild:

Bei der Zusammenführungssortierung sind zwei Dinge zu tun:

第一： “分”, 就是将数组尽可能的分，一直分到原子级别。

第二： “并”，将原子级别的数两两合并排序，最后产生结果。

代码：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace MergeSort
{
 class Program
 {
  static void Main(string[] args)
  {
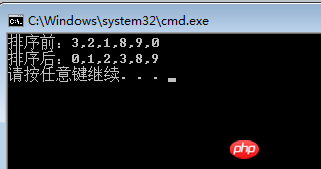
   int[] array = { 3, 2, 1, 8, 9, 0 };

   MergeSort(array, new int[array.Length], 0, array.Length - 1);

   Console.WriteLine(string.Join(",", array));
  }

  ///<summary>
/// 数组的划分
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时存放数组</param>
///<param name="left">序列段的开始位置，</param>
///<param name="right">序列段的结束位置</param>
  static void MergeSort(int[] array, int[] temparray, int left, int right)
  {
   if (left < right)
   {
    //取分割位置
    int middle = (left + right) / 2;

    //递归划分数组左序列
    MergeSort(array, temparray, left, middle);

    //递归划分数组右序列
    MergeSort(array, temparray, middle + 1, right);

    //数组合并操作
    Merge(array, temparray, left, middle + 1, right);
   }
  }

  ///<summary>
/// 数组的两两合并操作
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时数组</param>
///<param name="left">第一个区间段开始位置</param>
///<param name="middle">第二个区间的开始位置</param>
///<param name="right">第二个区间段结束位置</param>
  static void Merge(int[] array, int[] temparray, int left, int middle, int right)
  {
   //左指针尾
   int leftEnd = middle - 1;

   //右指针头
   int rightStart = middle;

   //临时数组的下标
   int tempIndex = left;

   //数组合并后的length长度
   int tempLength = right - left + 1;

   //先循环两个区间段都没有结束的情况
   while ((left <= leftEnd) && (rightStart <= right))
   {
    //如果发现有序列大，则将此数放入临时数组
    if (array[left] < array[rightStart])
     temparray[tempIndex++] = array[left++];
    else
     temparray[tempIndex++] = array[rightStart++];
   }

   //判断左序列是否结束
   while (left <= leftEnd)
    temparray[tempIndex++] = array[left++];

   //判断右序列是否结束
   while (rightStart <= right)
    temparray[tempIndex++] = array[rightStart++];

   //交换数据
   for (int i = 0; i < tempLength; i++)
   {
    array[right] = temparray[right];
    right--;
   }
  }
 }
}

结果图：

ps:

插入排序的时间复杂度为：O(N^2)

希尔排序的时间复杂度为：平均为：O(N^3/2)

最坏：O(N^2)

归并排序时间复杂度为： O(NlogN)

空间复杂度为: O(N)

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Grafikcodes des klassischen C#-Sortieralgorithmus (Teil 2). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!