Detaillierte Erläuterung des Grafikcodes des klassischen C#-Sortieralgorithmus (Teil 1)

In diesem Artikel wird hauptsächlich der erste Teil der Reihe von sieben klassischen Sortieralgorithmen in C#, Blasensortierung, Schnellsortierung usw. vorgestellt. Interessierte Freunde können darauf verweisen

Heute ist der Anfang des Artikels: Algorithmen sind wie Schwerter in der Programmentwicklung.

Für reale Sortierprobleme verfügt der Algorithmus über sieben scharfe Schwerter, die Ihnen zum Erfolg verhelfen können.

Zuallererst gibt es vier Arten der Sortierung:

Austauschsortierung: einschließlich Blasensortierung und Schnellsortierung.

Auswahlsortierung: einschließlich Direktauswahlsortierung und Heap-Sortierung.

Einfügungssortierung: einschließlich Direkteinfügungssortierung und Hill-Sortierung.

Sortierung zusammenführen: Sortierung zusammenführen.

Heute sprechen wir also über die Austauschsortierung. Wir alle wissen, dass die von der C#-Klassenbibliothek bereitgestellte Sortierung eine schnelle Sortierung ist.

Wir entwerfen einen Algorithmus um der Klassenbibliothek zu folgen. Bietet schnelle Warteschlangenschlachten. Kämpfe, um deinen Gegner KO zu schlagen.

Blasensortierung:

Lassen Sie uns zunächst die „Blasensortierung“ selbst entwerfen:

I Wenn Sie eine Handvoll Sand nehmen und ins Wasser geben, sinkt der Sand sofort auf den Grund des Wassers. Der Staub auf dem Sand sinkt aufgrund der Trägheit vorübergehend auf den Grund des Wassers, taucht aber sofort wie Blasen auf , und endlich wird die Wahrheit ans Licht kommen.

Was die sprudelnden Gedanken betrifft, werde ich weder über solche offiziellen Theorien sprechen, noch werde ich diese Worte veröffentlichen. Meine Gedanken sind nur beim Betrachten der Bilder.

Dann machen wir das Bild oben.

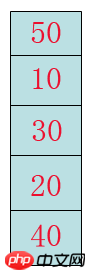
Um den sprudelnden Effekt zu erzielen, müssen wir eine Reihe von Zahlen aufstellen, um darüber nachzudenken. Wie Blase? Wie kann man verstehen, dass das Schwere zu Boden sinkt und das Leichte schwimmt?

Schritt eins: Wir vergleichen 40 mit 20 und stellen fest, dass 40 der Boss ist und kein Austausch nötig ist.

Der zweite Schritt: Dann machen Sie einen Schritt nach vorne, also vergleichen Sie 20 mit 30. Wenn Sie feststellen, dass 30 der Boss ist, müssen Sie tauschen.

Schritt 3: Vergleichen Sie die ausgetauschten 20 mit 10 und stellen Sie fest, dass Sie der Boss sind und keinen Austausch benötigen.

Schritt 4: Tauschen Sie 10 gegen 50. Sie finden, dass 50 der Boss ist, also tauschen Sie sie aus.

Endlich haben wir nach einem Durchlauf die kleinste Zahl im Array gesendet. Schauen Sie, wir sind dem Ziel einen weiteren Schritt näher gekommen.

Jetzt, da jeder weiß, was er denkt, werden wir dringend fordern, dass wir mit der schnellen Warteschlange konkurrieren. Entweder du stirbst oder ich überlebe.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;

namespace BubbleSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //五次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();
        //插入2k个随机数到数组中
        for (int j = 0; j < 2000; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 100000));
        }
        Console.WriteLine("\n第" + i + "次比较：");
        Stopwatch watch = new Stopwatch();
        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();
        Console.WriteLine("\n快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
        watch.Start();
        result = BubbleSort(list);
        watch.Stop();
        Console.WriteLine("\n冒泡排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
      }
    }

    //冒泡排序算法
    static List<int> BubbleSort(List<int> list)
    {
      int temp;
      //第一层循环： 表明要比较的次数，比如list.count个数，肯定要比较count-1次
      for (int i = 0; i < list.Count - 1; i++)
      {
        //list.count-1：取数据最后一个数下标，
//j>i: 从后往前的的下标一定大于从前往后的下标，否则就超越了。
        for (int j = list.Count - 1; j > i; j--)
        {
          //如果前面一个数大于后面一个数则交换
          if (list[j - 1] > list[j])
          {
            temp = list[j - 1];
            list[j - 1] = list[j];
            list[j] = temp;
          }
        }
      }
      return list;
    }
  }
}

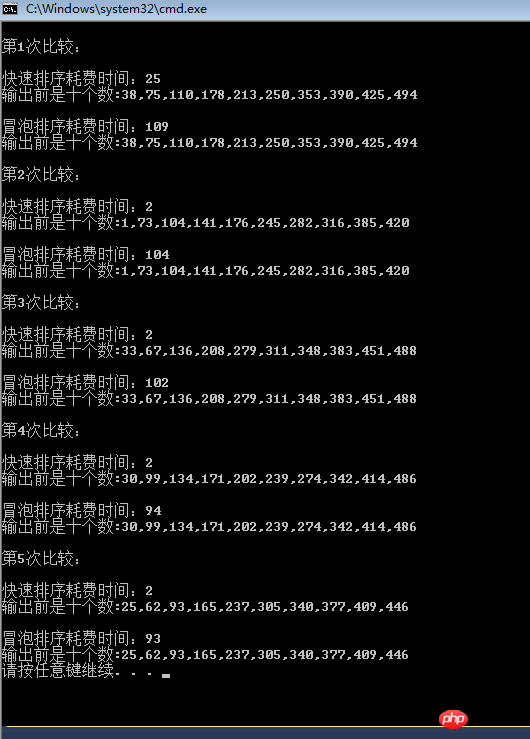
Ugh, als ich mir diese beiden sortierten Untersuchungsberichte ansah, wurde mir das Herz kalt, ich brodelte und war KO Das schnelle Ranking. Wow, es ist so miserabel, dass die Leute sagen, dass die Sprudeleffizienz niedrig ist, aber es stellt sich heraus, dass sie wirklich niedrig ist.

Schnelle Sortierung:

Da wir Sprudeln KO können, war unser Interesse sofort geweckt. Schnelle Sortierung ist so schnell, dass wir sie sorgfältig studieren müssen.

Zuerst das obige Bild:

Auf dem Bild können wir sehen:

linker Zeiger, rechter Zeiger, Basisreferenz Nummer.

Tatsächlich ist die Idee recht einfach: Sie besteht darin, den Schnittpunkt des Arrays durch den ersten Durchlauf zu finden (wodurch der linke und der rechte Zeiger zusammenfallen).

Schritt 1: Zuerst nehmen wir die Zahl (20) von der linken Position des Arrays als Basisreferenzobjekt.

Schritt 2: Suchen Sie vorwärts von der rechten Position des Arrays, bis Sie eine Zahl kleiner als (Basis) finden.

Wenn Sie diese Zahl finden, weisen Sie sie der linken Position zu (d. h. 10). Zugeordnet zu 20),

Zu diesem Zeitpunkt ist das Array: 10, 40, 50, 10, 60,

Der linke und der rechte Zeiger sind jeweils 10 davor und danach.

Schritt 3: Suchen Sie von der linken Position des Arrays rückwärts, bis Sie eine Zahl finden, die größer als (Basis) ist.

Wenn Sie diese Zahl finden, weisen Sie sie der rechten Position zu (d. h. 40). Zu 10),

Zu diesem Zeitpunkt ist das Array: 10, 40, 50, 40, 60,

Der linke und der rechte Zeiger sind jeweils 40 davor und danach.

Schritt 4: Wiederholen Sie den „zweiten, dritten“ Schritt, bis der linke und rechte Zeiger übereinstimmen,

schließlich (Basis) an 40 Positionen einfügen,

Zu diesem Zeitpunkt das Array Werte sind: 10, 20, 50, 40, 60. An diesem Punkt ist eine Sortierung abgeschlossen.

Schritt 5: Zu diesem Zeitpunkt hat sich 20 in das Innere des Arrays eingeschlichen. Die Zahlengruppe auf der linken Seite von 20 ist kleiner als 20 und die Zahlengruppe auf der rechten Seite von 20 ist kleiner größer als 20.

            以20为切入点对左右两边数按照"第一，第二，第三，第四"步骤进行，最终快排大功告成。 

同样，我们把自己设计的快排跟类库提供的快拍比较一下。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace QuickSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //5次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();

        //插入200个随机数到数组中
        for (int j = 0; j < 200; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 10000));
        }

        Console.WriteLine("\n第" + i + "次比较：");

        Stopwatch watch = new Stopwatch();

        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();

        Console.WriteLine("\n系统定义的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));

        watch.Start();
        new QuickSortClass().QuickSort(list, 0, list.Count - 1);
        watch.Stop();

        Console.WriteLine("\n俺自己写的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", list.Take(10).ToList()));

      }
    }
  }

  public class QuickSortClass
  {

    ///<summary>
/// 分割函数
///</summary>
///<param name="list">待排序的数组</param>
///<param name="left">数组的左下标</param>
///<param name="right"></param>
///<returns></returns>
    public int pision(List<int> list, int left, int right)
    {
      //首先挑选一个基准元素
      int baseNum = list[left];

      while (left < right)
      {
        //从数组的右端开始向前找，一直找到比base小的数字为止(包括base同等数)
        while (left < right && list[right] >= baseNum)
          right = right - 1;

        //最终找到了比baseNum小的元素，要做的事情就是此元素放到base的位置
        list[left] = list[right];

        //从数组的左端开始向后找，一直找到比base大的数字为止（包括base同等数）
        while (left < right && list[left] <= baseNum)
          left = left + 1;


        //最终找到了比baseNum大的元素，要做的事情就是将此元素放到最后的位置
        list[right] = list[left];
      }
      //最后就是把baseNum放到该left的位置
      list[left] = baseNum;

      //最终，我们发现left位置的左侧数值部分比left小，left位置右侧数值比left大
//至此，我们完成了第一篇排序
      return left;
    }

    public void QuickSort(List<int> list, int left, int right)
    {
      //左下标一定小于右下标，否则就超越了
      if (left < right)
      {
        //对数组进行分割，取出下次分割的基准标号
        int i = pision(list, left, right);

        //对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, left, i - 1);

        //对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, i + 1, right);
      }
    }
  }
}

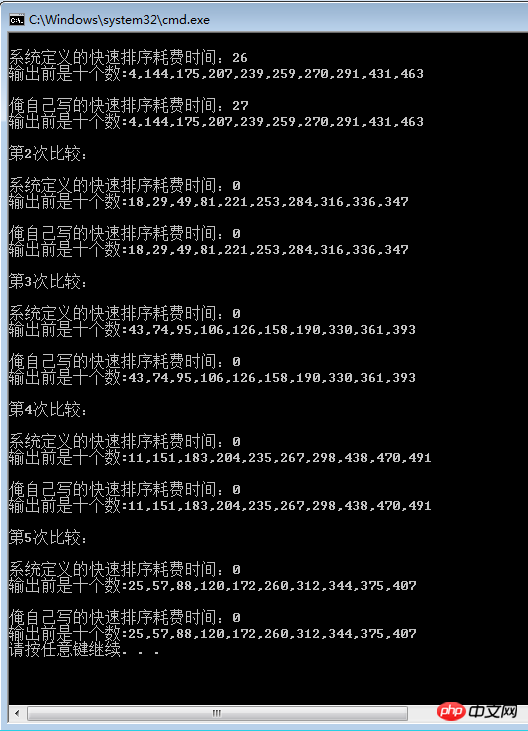
不错，快排就是快，难怪内库非要用他来作为排序的标准。 

嗯，最后要分享下：

冒泡的时间复杂度为：0(n) - 0(n^2)

快排的时间复杂度为：

    平均复杂度：N(logN)

    最坏复杂度： 0(n^2)

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Grafikcodes des klassischen C#-Sortieralgorithmus (Teil 1). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!