Heim >Web-Frontend >H5-Tutorial >Detaillierte Erläuterung des Grafik- und Textcodes für die Darstellung eines 3D-Netzwerktopologiebaums auf Basis von HTML5
Detaillierte Erläuterung des Grafik- und Textcodes für die Darstellung eines 3D-Netzwerktopologiebaums auf Basis von HTML5
- 黄舟Original
- 2017-03-07 15:36:481938Durchsuche
In HT für Web unterstützen sowohl 2D- als auch 3D-Anwendungen die Anzeige von Baumstrukturdaten mit unterschiedlichen Anzeigeeffekten. Die Baumstruktur in 2D weist eine offensichtliche hierarchische Beziehung auf, wenn jedoch die Datenmenge unterschiedlich ist groß, es scheint nicht so intuitiv zu sein und es ist schwieriger, den angegebenen Knoten zu finden. In Kombination mit der elastischen Layoutkomponente von HT für Web wird die Baumstruktur jedoch intuitiver angezeigt Daten auf einen Blick, aber unter dem Einfluss des elastischen Layouts ist seine hierarchische Struktur nicht so klar. Zu diesem Zeitpunkt besteht also Bedarf an einem 3D-Baum mit einer klaren Struktur. Wie genau sieht dieser 3D-Baum aus?
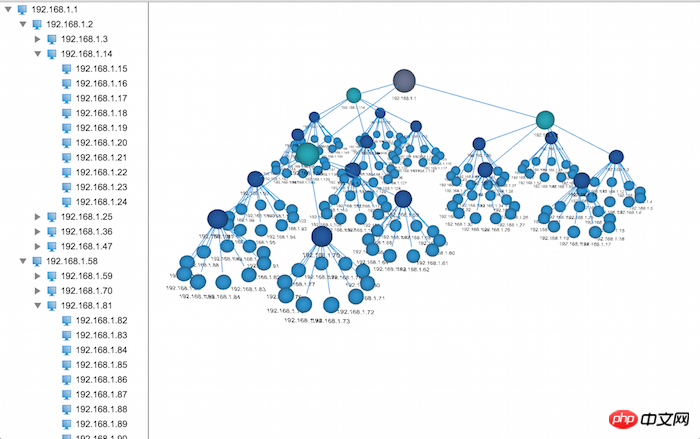
Um dies zu erreichen Wirkung, wo soll ich anfangen? Als nächstes werden wir dieses Problem in mehrere kleine zu lösende Probleme zerlegen.
1. Erstellen Sie eine Baumstruktur
Diejenigen, die etwas über HT für Web gelernt haben, sollten mit der Erstellung von Baumstrukturdaten vertraut sein, daher werde ich hier nicht näher darauf eingehen. Das Erstellen von Baumstrukturdaten ist sehr einfach. Um den Code prägnanter zu gestalten, habe ich drei Methoden zum Erstellen von Baumstrukturdaten gekapselt:
/**
* 创建连线
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} source - 起点
* @param {ht.Node} target - 终点
*/
function createEdge(dataModel, source, target) {
// 创建连线,链接父亲节点及孩子节点
var edge = new ht.Edge();
edge.setSource(source);
edge.setTarget(target);
dataModel.add(edge);
}
/**
* 创建节点对象
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} [parent] - 父亲节点
* @returns {ht.Node} 节点对象
*/
function createNode(dataModel, parent) {
var node = new ht.Node();
if (parent) {
// 设置父亲节点
node.setParent(parent);
createEdge(dataModel, parent, node);
}
// 添加到数据容器中
dataModel.add(node);
return node;
}
/**
* 创建结构树
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} parent - 父亲节点
* @param {Number} level - 深度
* @param {Array} count - 每层节点个数
* @param {function(ht.Node, Number, Number)} callback - 回调函数(节点对象,节点对应的层级,节点在层级中的编号)
*/
function createTreeNodes(dataModel, parent, level, count, callback) {
level--;
var num = (typeof count === 'number' ? count : count[level]);
while (num--) {
var node = createNode(dataModel, parent);
// 调用回调函数,用户可以在回调里面设置节点相关属性
callback(node, level, num);
if (level === 0) continue;
// 递归调用创建孩子节点
createTreeNodes(dataModel, node, level, count, callback);
}
}Hey, der Code könnte sein Ein wenig geschrieben. Der einfache Weg besteht darin, mehrere For-Schleifen zu verschachteln. Ich werde hier nicht auf Details eingehen.
2. Simulieren Sie die Radiusberechnung jeder Schicht der 3D-Baumstruktur unter 2D-Topologie
Das größte Problem bei der Baumstruktur unter 3D besteht darin, dass die Ebene jedes Knotens und jeder Schicht ein Knoten ist Der Radius wird um den übergeordneten Knoten herum berechnet. Da nun die Baumstrukturdaten verfügbar sind, ist es an der Zeit, mit der Berechnung des Radius zu beginnen. Wir beginnen mit der zweischichtigen Baumstruktur:

Ich erstelle jetzt zwei Schichten Baumstruktur: Alle untergeordneten Knoten sind in einer Reihe angeordnet und umgeben ihre übergeordneten Knoten nicht. Wie bestimmen wir also die Positionen dieser untergeordneten Knoten?
Zunächst müssen wir wissen, dass jeder Endknoten einen Kreis seiner eigenen Domäne hat, da es sonst zu Überlappungen zwischen den Knoten kommt. Daher gehen wir hier davon aus, dass der Domänenradius des Endknotens 25 beträgt. Dann beträgt der kürzeste Abstand zwischen zwei benachbarten Knoten das Doppelte des Knotenfeldradius, der 50 beträgt, und diese Endknoten umgeben ihre übergeordneten Knoten gleichmäßig, sodass der Öffnungswinkel der beiden benachbarten Knoten bestätigt werden kann. Kommen Sie mit dem Öffnungswinkel heraus und der Abstand zwischen den beiden Punkten, der kürzeste Radius des Knotens um seinen übergeordneten Knoten, kann ebenfalls berechnet werden. Angenommen, der Öffnungswinkel ist a und der Mindestabstand zwischen den beiden Punkten ist b, dann lautet der Mindestradius r. Die Berechnungsformel lautet:
r = b / 2 / sin(a / 2);
Dann lasst uns den Baum so schreiben:
/**
* 布局树
* @param {ht.Node} root - 根节点
* @param {Number} [minR] - 末端节点的最小半径
*/
function layout(root, minR) {
// 设置默认半径
minR = (minR == null ? 25 : minR);
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = Math.PI * 2 / len;
// 根据三角函数计算绕父亲节点的半径
var sin = Math.sin(degree / 2),
r = minR / sin;
// 获取父亲节点的位置坐标
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 设置孩子节点的位置坐标
child.p(x + rootPosition.x, y + rootPosition.y);
});
}Im Im Code werden Sie feststellen, dass ich den Endradius standardmäßig auf 25 eingestellt habe. Auf diese Weise können wir den Strukturbaum durch Aufrufen der Methode „layout()“ wie folgt gestalten:

Wie aus den Darstellungen hervorgeht, ist der Standardradius der Endknoten nicht sehr ideal. Die Layouteffektlinien sind nahezu unsichtbar, sodass wir den Standardradius der Endknoten vergrößern können Wenn beispielsweise das Problem eines zu dichten Layouts besteht, hat das Festlegen des Standardradius auf 40 folgende Auswirkungen:
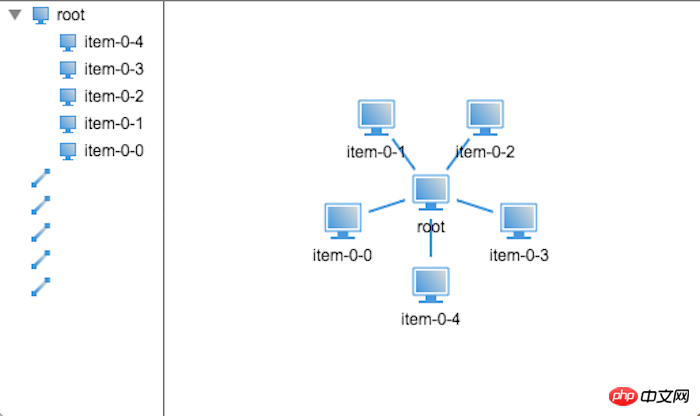
Da nun die zweischichtige Baumverteilung gelöst ist, nehmen wir Folgendes an Schauen Sie sich an, wie Sie mit der dreischichtigen Baumverteilung umgehen.
Wenn man die zweite und dritte Schicht als Ganzes betrachtet, ist die Baumstruktur der drei Schichten tatsächlich dieselbe wie die der beiden Schichten. Der Unterschied besteht darin, dass sie bei der Verarbeitung der Knoten der zweiten Schicht identisch sein sollten Um eine zweischichtige Baumstruktur zu verarbeiten, ist Rekursion der beste Weg, mit dieser Art von Regelmäßigkeit umzugehen. Daher werden wir den Code ein wenig ausprobieren und sehen, wie er funktioniert:
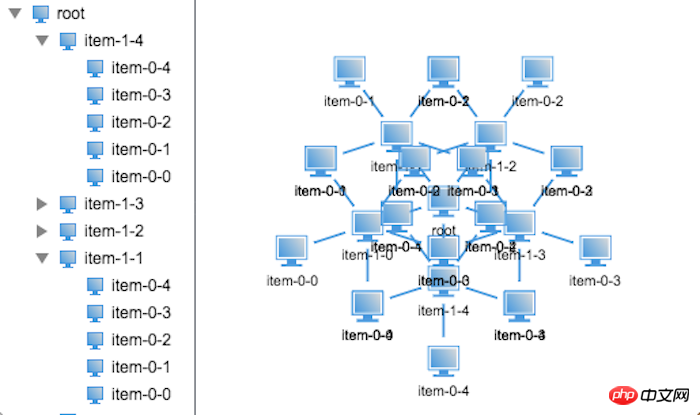
Nein, die Knoten überlappen sich alle. Es scheint, dass eine einfache Rekursion nicht funktioniert. Wo liegt also das konkrete Problem?
Nach sorgfältiger Analyse habe ich herausgefunden, dass der Domänenradius des Vaterknotens durch den Domänenradius seines untergeordneten Knotens bestimmt wird. Daher müssen Sie beim Layout den Domänenradius Ihres eigenen Knotens kennen des Knotens hängt von der Domäne des übergeordneten Knotens und den Positionsinformationen ab, sodass die Knotenposition bei der Berechnung des Radius nicht angegeben werden kann.
Jetzt können wir nur noch die Berechnung des Radius vom Layout trennen und einen zweistufigen Vorgang durchführen. Analysieren wir zunächst die Berechnung des Knotenradius:
Zuerst müssen wir das Wesentliche klären Kritische Bedingungen, Vater Der Radius eines Knotens hängt vom Radius seines untergeordneten Knotens ab. Diese Bedingung besagt, dass der Knotenradius nur von unten nach oben berechnet werden kann. Daher muss die rekursive Funktion, die wir entwerfen, zuerst rekursiv sein und dann berechnet werden. Werfen wir ohne weiteres einen Blick auf die Einzelheiten der Code-Implementierung:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的半径
var pRadius = radius / Math.sin(degree);
// 设置父亲节点的半径及其孩子节点的布局张角
root.a('radius', pRadius);
root.a('degree', degree * 2);
}OK,半径的计算解决了,那么接下来就该解决布局问题了,布局树状结构数据需要明确:孩子节点的坐标位置取决于其父亲节点的坐标位置,因此布局的递归方式和计算半径的递归方式不同,我们需要先布局父亲节点再递归布局孩子节点,具体看看代码吧:
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 设置孩子节点的位置坐标
child.p(x + rootPosition.x, y + rootPosition.y);
// 递归调用布局孩子节点
layout(child);
});
}代码写完了,接下来就是见证奇迹的时刻了,我们来看看效果图吧:
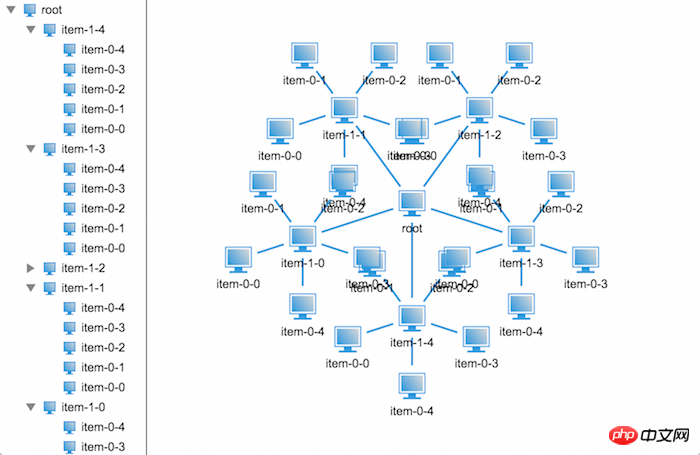
不对呀,代码应该是没问题的呀,为什么显示出来的效果还是会重叠呢?不过仔细观察我们可以发现相比上个版本的布局会好很多,至少这次只是末端节点重叠了,那么问题出在哪里呢?
不知道大家有没有发现,排除节点自身的大小,倒数第二层节点与节点之间的领域是相切的,那么也就是说节点的半径不仅和其孩子节点的半径有关,还与其孙子节点的半径有关,那我们把计算节点半径的方法改造下,将孙子节点的半径也考虑进去再看看效果如何,改造后的代码如下:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
……
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
var child00 = child0.getChildAt(0);
// 半径加上孙子节点半径,避免节点重叠
if (child00) radius += child00.a('radius');
……
}下面就来看看效果吧~
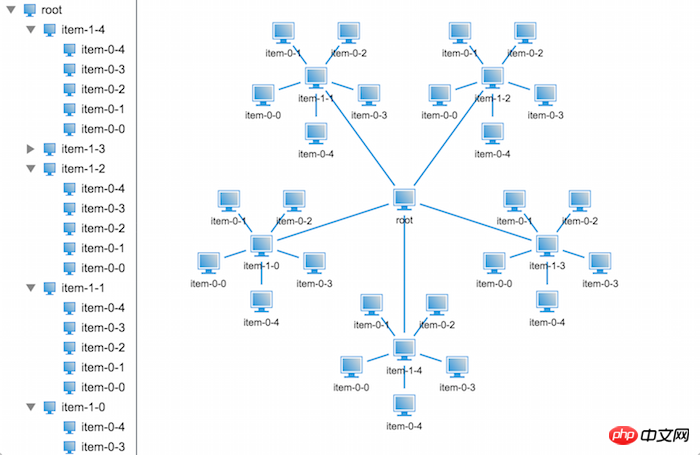
哈哈,看来我们分析对了,果然就不再重叠了,那我们来看看再多一层节点会是怎么样的壮观场景呢?

哦,NO!这不是我想看到的效果,又重叠了,好讨厌。
不要着急,我们再来仔细分析分析下,在前面,我们提到过一个名词——领域半径,什么是领域半径呢?很简单,就是可以容纳下自身及其所有孩子节点的最小半径,那么问题就来了,末端节点的领域半径为我们指定的最小半径,那么倒数第二层的领域半径是多少呢?并不是我们前面计算出来的半径,而应该加上末端节点自身的领域半径,因为它们之间存在着包含关系,子节点的领域必须包含于其父亲节点的领域中,那我们在看看上图,是不是感觉末端节点的领域被侵占了。那么我们前面计算出来的半径代表着什么呢?前面计算出来的半径其实代表着孩子节点的布局半径,在布局的时候是通过该半径来布局的。
OK,那我们来总结下,节点的领域半径是其下每层节点的布局半径之和,而布局半径需要根据其孩子节点个数及其领域半径共同决定。
好了,我们现在知道问题的所在了,那么我们的代码该如何去实现呢?接着往下看:
/**
* 就按节点领域半径及布局半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其布局半径及领域半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
root.a('totalRadius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius'),
totalRadius = child0.a('totalRadius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的布局半径
var pRadius = totalRadius / Math.sin(degree);
// 缓存父亲节点的布局半径
root.a('radius', pRadius);
// 缓存父亲节点的领域半径
root.a('totalRadius', pRadius + totalRadius);
// 缓存其孩子节点的布局张角
root.a('degree', degree * 2);
}在代码中我们将节点的领域半径缓存起来,从下往上一层一层地叠加上去。接下来我们一起验证其正确性:
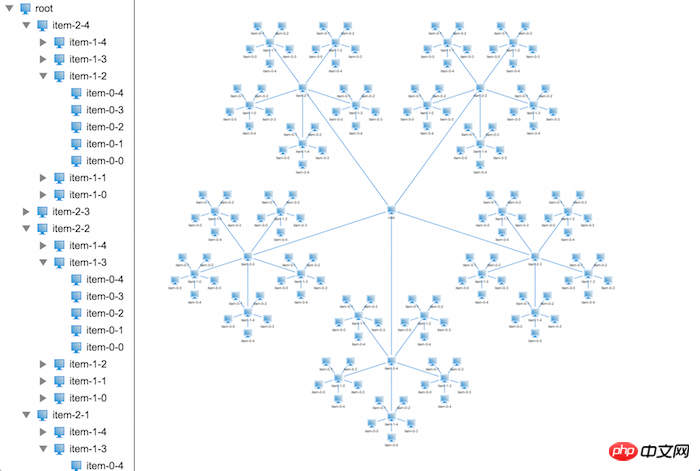
搞定,就是这样子了,2D拓扑上面的布局搞定了,那么接下来该出动3D拓扑啦~
3. 加入z轴坐标,呈现3D下的树状结构
3D拓扑上面布局无非就是多加了一个坐标系,而且这个坐标系只是控制节点的高度而已,并不会影响到节点之间的重叠,所以接下来我们来改造下我们的程序,让其能够在3D上正常布局。
也不需要太大的改造,我们只需要修改下布局器并且将2D拓扑组件改成3D拓扑组件就可以了。
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p3();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
z = c * r;
// 设置孩子节点的位置坐标
child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);
// 递归调用布局孩子节点
layout(child);
});
}上面是改造成3D布局后的布局器代码,你会发现和2D的布局器代码就差一个坐标系的的计算,其他的都一样,看下在3D上布局的效果:
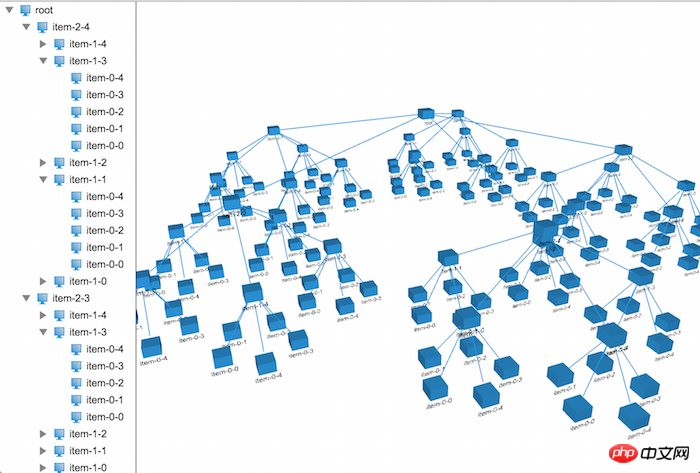
恩,有模有样的了,在文章的开头,我们可以看到每一层的节点都有不同的颜色及大小,这些都是比较简单,在这里我就不做深入的讲解,具体的代码实现如下:
var level = 4,
size = (level + 1) * 20;
var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);
root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);
var colors = {},
sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
if (!colors[level]) {
colors[level] = randomColor();
sizes[level] = (level + 1) * 20;
}
size = sizes[level];
data.setName('item-' + level + '-' + num);
// 设置节点形状为球形
data.s('shape3d', 'sphere');
data.s('shape3d.color', colors[level]);
data.s3(size, size, size);
});在这里引入了一个随机生成颜色值的方法,对每一层随机生成一种颜色,并将节点的形状改成了球形,让页面看起来美观些(其实很丑)。
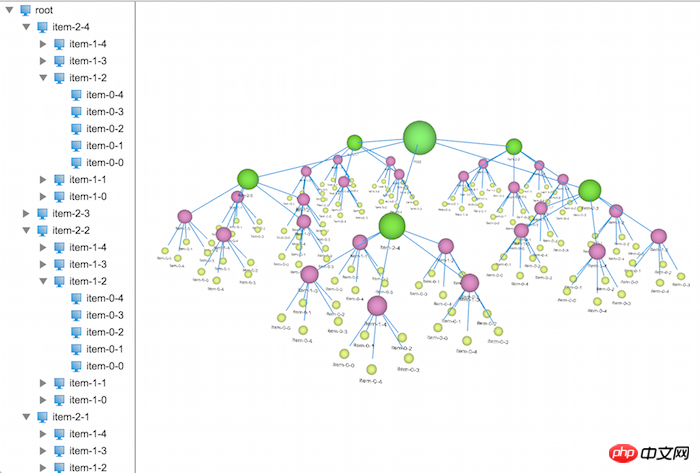
提个外话,节点上可以贴上图片,还可以设置文字的朝向,可以根据用户的视角动态调整位置,等等一系列的拓展,这些大家都可以去尝试,相信都可以做出一个很漂亮的3D树出来。
到此,整个Demo的制作就结束了,今天的篇幅有些长,感谢大家的耐心阅读,在设计上或则是表达上有什么建议或意见欢迎大家提出,点击这里可以访问HT for Web官网上的手册。
Das Obige ist die detaillierte Erläuterung des grafischen Codes des 3D-Netzwerktopologiebaums basierend auf HTML5. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.cn).
In Verbindung stehende Artikel
Mehr sehen- Das Vollbild-Bildlauf-Plug-in AlloyTouch erstellt in 30 Sekunden eine flüssige H5-Seite
- Tatsächlicher HTML5-Kampf und Analyse von Touch-Ereignissen (Touchstart, Touchmove und Touchend)
- Ausführliche Erläuterung der Beispiele für Bildzeichnungen in HTML5 Canvas 9
- Reguläre Ausdrücke und neue HTML5-Elemente
- So kombinieren Sie NodeJS und HTML5, um mehrere Dateien per Drag-and-Drop auf den Server hochzuladen

