Verwenden Sie Python, um verschiedene Sortieralgorithmen zu implementieren

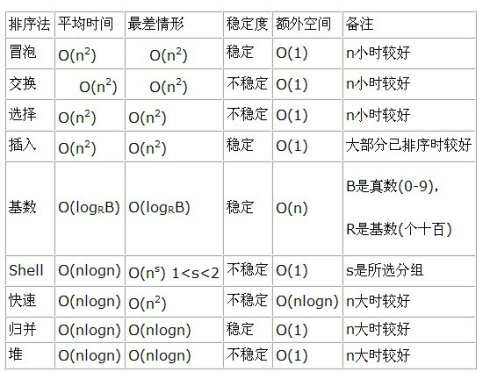
Eine Zusammenfassung gängiger zentralisierter Sortieralgorithmen

Zusammenführungssortierung

Zusammenführungssortierung, auch Zusammenführungssortierung genannt, ist eine typische Anwendung des Teilens und -conquer-Methode. Die Idee von „Teile und herrsche“ besteht darin, jedes Problem in kleine Probleme zu zerlegen, jedes kleine Problem zu lösen und sie dann zusammenzuführen.

Die spezifische Zusammenführungssortierung besteht darin, eine Menge ungeordneter Zahlen rekursiv in Unterelemente mit nur einem Element um n/2 zu zerlegen, und ein Element ist bereits sortiert. Anschließend werden diese geordneten Unterelemente zusammengeführt.

Der Zusammenführungsprozess besteht darin, zwei sortierte Teilsequenzen zu vergleichen, zuerst das kleinste Element in den beiden Teilsequenzen auszuwählen, dann die kleinste Teilsequenz der beiden Elemente auszuwählen und es aus der Teilsequenz zu entfernen

Entfernen und Zum endgültigen Ergebnissatz hinzufügen, bis die beiden Teilsequenzen zusammengeführt sind.

Der Code lautet wie folgt:

#!/usr/bin/python  
import sys  
   
def merge(nums, first, middle, last):  
    ''''' merge '''  
    # 切片边界,左闭右开并且是了0为开始  
    lnums = nums[first:middle+1]   
    rnums = nums[middle+1:last+1]  
    lnums.append(sys.maxint)  
    rnums.append(sys.maxint)  
    l = 0  
    r = 0  
    for i in range(first, last+1):  
        if lnums[l] < rnums[r]:  
            nums[i] = lnums[l]  
            l+=1  
        else:  
            nums[i] = rnums[r]  
            r+=1  
def merge_sort(nums, first, last):  
    &#39;&#39;&#39;&#39;&#39; merge sort 
    merge_sort函数中传递的是下标，不是元素个数 
    &#39;&#39;&#39;  
    if first < last:  
        middle = (first + last)/2  
        merge_sort(nums, first, middle)  
        merge_sort(nums, middle+1, last)  
        merge(nums, first, middle,last)  
   
if __name__ == &#39;__main__&#39;:  
    nums = [10,8,4,-1,2,6,7,3]  
    print &#39;nums is:&#39;, nums  
    merge_sort(nums, 0, 7)  
    print &#39;merge sort:&#39;, nums

Stabil, zeitliche Komplexität O(nlog n)

Einfügungssortierung

Der Code lautet wie folgt:

#!/usr/bin/python  
import sys  
   
def insert_sort(a):  
    ''''' 插入排序 
    有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数， 
    但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序，然后插入一 
    个元素到适当位置，然后再插入第三个元素，依次类推 
    '''  
    a_len = len(a)  
    if a_len = 0 and a[j] > key:  
            a[j+1] = a[j]  
            j-=1  
        a[j+1] = key  
    return a  
   
if __name__ == '__main__':  
    nums = [10,8,4,-1,2,6,7,3]  
    print 'nums is:', nums  
    insert_sort(nums)  
    print 'insert sort:', nums

Stabil, zeitliche Komplexität O(n^2)

Austausch zwei Elemente In Python können Sie schreiben: a, b = b, a. Tatsächlich liegt dies daran, dass die linke und rechte Seite des Zuweisungssymbols Tupel sind

(hier muss betont werden, dass in Python , Tupel werden tatsächlich durch Kommas "," anstelle von Klammern getrennt.

Auswahlsortierung

Auswahlsortierung ist ein einfacher und intuitiver Sortieralgorithmus. So funktioniert es. Suchen Sie zunächst das kleinste (große) Element in der unsortierten Sequenz und speichern Sie es an der Startposition der

sortierten Sequenz. Suchen Sie dann weiterhin das kleinste (große) Element aus den verbleibenden unsortierten Elementen und Fügen Sie es dann in die sortierte Reihenfolge ein. Und so weiter, bis alle

-Elemente sortiert sind.

import sys  
def select_sort(a):  
    ''''' 选择排序  
    每一趟从待排序的数据元素中选出最小（或最大）的一个元素， 
    顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。 
    选择排序是不稳定的排序方法。 
    '''  
    a_len=len(a)  
    for i in range(a_len):#在0-n-1上依次选择相应大小的元素   
        min_index = i#记录最小元素的下标   
        for j in range(i+1, a_len):#查找最小值  
            if(a[j]<a[min_index]):  
                min_index=j  
        if min_index != i:#找到最小元素进行交换  
            a[i],a[min_index] = a[min_index],a[i]  
   
if __name__ == &#39;__main__&#39;:  
    A = [10, -3, 5, 7, 1, 3, 7]    
    print &#39;Before sort:&#39;,A    
    select_sort(A)    
    print &#39;After sort:&#39;,A

Instabil, zeitliche Komplexität O(n^2)

Hill-Sortierung

Hill-Sortierung, auch bekannt Als absteigender inkrementeller Sortieralgorithmus ist die Hill-Sortierung ein instabiler Sortieralgorithmus. Diese Methode wird auch als reduzierende inkrementelle Sortierung bezeichnet, da DL. Shell wurde nach seinem Vorschlag im Jahr 1959 benannt.

Nehmen Sie zunächst eine Ganzzahl d1 kleiner als n als erstes Inkrement und teilen Sie alle Datensätze in der Datei in d1-Gruppen auf. Alle Datensätze, deren Abstand ein Vielfaches von d1 ist, werden in derselben Gruppe platziert. Sortieren Sie zuerst innerhalb jeder Gruppe;

Nehmen Sie dann das zweite Inkrement d2

import sys  
def shell_sort(a):  
    ''''' shell排序  
    '''  
    a_len=len(a)  
    gap=a_len/2#增量  
    while gap>0:  
        for i in range(a_len):#对同一个组进行选择排序  
            m=i  
            j=i+1  
            while j<a_len:  
                if a[j]<a[m]:  
                    m=j  
                j+=gap#j增加gap  
            if m!=i:  
                a[m],a[i]=a[i],a[m]  
        gap/=2  
   
if __name__ == &#39;__main__&#39;:  
    A = [10, -3, 5, 7, 1, 3, 7]    
    print &#39;Before sort:&#39;,A    
    shell_sort(A)    
    print &#39;After sort:&#39;,A

Instabil, Zeitkomplexität durchschnittliche Zeit O(nlogn) schlechteste Zeit O(n^s)1

Heap-Sortierung (Heap-Sortierung)

Definition von „Heap“: Im „Heap“ mit einem Startindex von 0:

Der rechte untergeordnete Knoten von Knoten i befindet sich an Position 2 * i 24 ) Der übergeordnete Knoten von Knoten i befindet sich an der Position floor((i - 1) / 2): Beachten Sie, dass floor die „Rundungs“-Operation darstellt

Eigenschaften des Heaps:

Schlüsselwert von Jeder Knoten muss immer größer (oder kleiner) als sein übergeordneter Knoten sein

„Max Heap“:

Der Wurzelknoten des „Heaps“ speichert den Knoten mit dem größten Schlüsselwert. Das heißt, der Schlüsselwert jedes Knotens im „Heap“ ist immer größer als der seiner untergeordneten Knoten.

Nach oben verschieben, nach unten verschieben:

Wenn der Schlüsselwert eines Knotens größer als sein übergeordneter Knoten ist, müssen wir eine „Nach oben“-Operation durchführen, das heißt, wir verschieben den Knoten zu Die Position seines übergeordneten Knotens,

und lassen Sie seinen übergeordneten Knoten seine Position erreichen, und dann beurteilen wir den Knoten weiter und hören nicht auf, uns nach oben zu bewegen, bis der Knoten nicht mehr größer als sein ist übergeordneter Knoten.

Jetzt werfen wir einen Blick auf den Vorgang „Nach unten verschieben“. Wenn wir den Schlüsselwert eines Knotens auf einen kleineren Wert ändern, müssen wir ihn „nach unten verschieben“.

Methode:

Wir erstellen zunächst einen maximalen Heap (Zeitkomplexität O(n)) und müssen dann jedes Mal nur den Wurzelknoten mit dem Knoten an der letzten Position austauschen, und Dann setzen Sie die letzte Eine Position wird ausgeschlossen, und dann wird der Heap des Wurzelknotens nach dem Austausch angepasst (Zeitkomplexität O(lgn)), dh der Wurzelknoten wird „nach unten verschoben“. Die Gesamtzeitkomplexität der Heap-Sortierung beträgt O(nlgn). Der Code lautet wie folgt:

#!/usr/bin env python  
   
# 数组编号从 0开始  
def left(i):  
    return 2*i +1  
def right(i):  
    return 2*i+2  
   
#保持最大堆性质 使以i为根的子树成为最大堆  
def max_heapify(A, i, heap_size):  
    if heap_size <= 0:  
        return   
    l = left(i)  
    r = right(i)  
    largest = i # 选出子节点中较大的节点  
    if l  A[largest]:  
        largest = l  
    if r  A[largest]:  
        largest = r  
    if i != largest :#说明当前节点不是最大的，下移  
        A[i], A[largest] = A[largest], A[i] #交换  
        max_heapify(A, largest, heap_size)#继续追踪下移的点  
    #print A  
# 建堆    
def bulid_max_heap(A):  
    heap_size = len(A)  
    if heap_size >1:  
        node = heap_size/2 -1  
        while node >= 0:  
           max_heapify(A, node, heap_size)  
           node -=1  
   
# 堆排序 下标从0开始  
def heap_sort(A):  
    bulid_max_heap(A)  
    heap_size = len(A)  
    i = heap_size - 1   
    while i > 0 :  
        A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置，并且进行交换  
        heap_size -=1 # heap 大小 递减 1  
        i -= 1 # 存放堆中最大值的下标递减 1  
        max_heapify(A, 0, heap_size)  
   
if __name__ == &#39;__main__&#39; :  
   
    A = [10, -3, 5, 7, 1, 3, 7]  
    print &#39;Before sort:&#39;,A  
    heap_sort(A)  
    print &#39;After sort:&#39;,A

Instabile Zeitkomplexität O(nlog n)

Schnellsortierung

Der Schnellsortierungsalgorithmus basiert ebenso wie der Zusammenführungssortierungsalgorithmus auf dem Divide-and-Conquer-Modell. Die drei Schritte des Divide-and-Conquer-Prozesses zum schnellen Sortieren des Subarrays A[p...r] sind:

Zerlegung: Teilen Sie das Array A[p...r] in A[p. ..q -1] und A[q 1...r], wobei jedes Element in A[p...q-1] kleiner oder gleich A[q] ist und in A[q 1... r] Jedes Element von ist größer oder gleich A[q];

Lösung: Rufen Sie die schnelle Sortierung rekursiv für die Subarrays A[p...q-1] und A[q 1...r auf ] Sortieren;

Zusammenführen: Da die beiden Subarrays an Ort und Stelle sortiert sind, sind keine zusätzlichen Vorgänge erforderlich.

Für den Anfang jeder Iteration der Partitionspartition, x=A[r], für jeden Array-Index k gibt es:

1) Wenn p≤k≤i, dann A[ k]≤x.

2) Wenn i 1≤k≤j-1, dann A[k]>x.

3) Wenn k=r, dann A[k]=x.

Der Code lautet wie folgt:

Instabil, die beste Zeitkomplexität ist O(nlogn) und die schlechteste Zeit ist O(n^2)

Lassen Sie uns über Sequenzen in Python sprechen:

Listen, Tupel und Strings Das ist es alles Sequenzen, aber was sind Sequenzen und warum sind sie so besonders? Die beiden Hauptmerkmale von Sequenzen sind der Indexierungsoperator und der Slicing-Operator. Mit dem Indexoperator können wir ein bestimmtes Element aus einer Sequenz abrufen. Mit dem Slice-Operator können wir einen Slice der Sequenz erhalten, dh einen Teil der Sequenz, wie zum Beispiel: a = ['aa', 'bb', 'cc'], print a[0] ist eine Indexoperation , drucken Sie a[0:2] für Slicing-Operationen.