Warum wusste ich beim Erlernen der Liniengenerierung nicht: Es gibt eine Äquivalenzbeziehung zwischen Matrizen und Graphen?

Die Matrix ist schwer zu verstehen, kann aber aus einer anderen Perspektive anders sein.

Wenn wir Mathematik lernen, sind wir oft frustriert über die Schwierigkeit und Abstraktheit des gelernten Wissens, aber manchmal können wir einfach durch einen Perspektivenwechsel eine einfache und intuitive Lösung für das Problem finden. Als wir zum Beispiel als Kinder die Formel der Quadratsumme (a+b)² lernten, verstehen wir vielleicht nicht, warum sie gleich a²+2ab+b² ist. Wir wissen nur, dass sie in der Formel so geschrieben ist Buch und der Lehrer baten uns, uns das so zu merken; bis wir eines Tages dieses animierte Bild sahen:

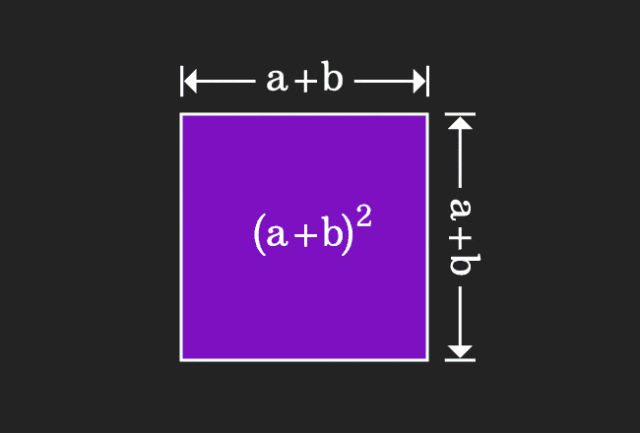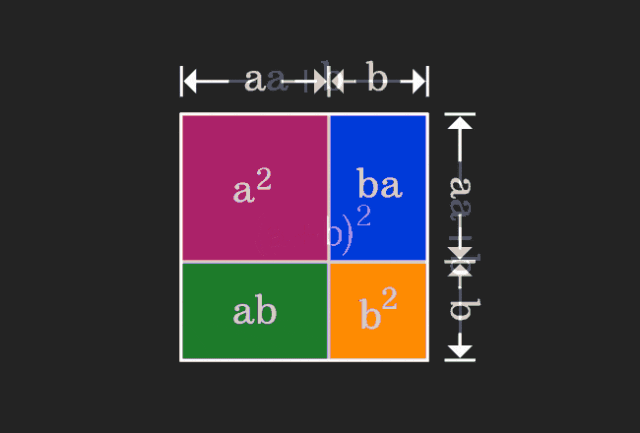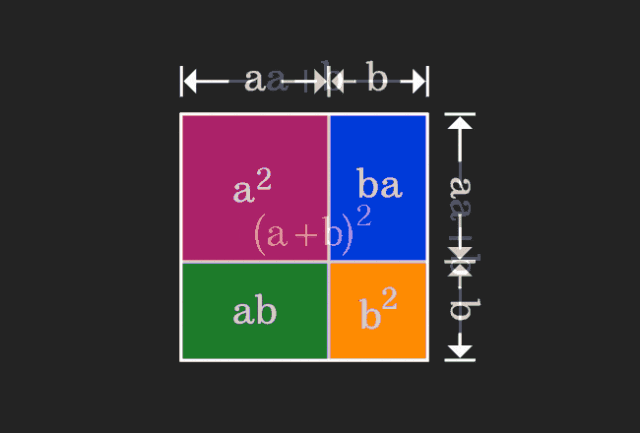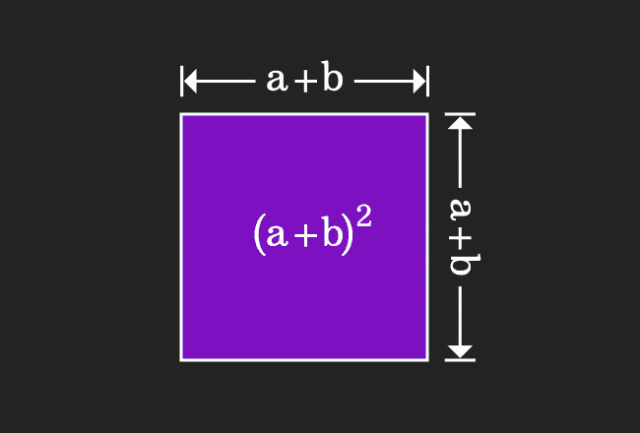
Mir wurde plötzlich klar, dass wir es aus einer geometrischen Perspektive verstehen können!

Jetzt taucht dieses Gefühl der Erleuchtung wieder auf: Die nichtnegative Matrix kann äquivalent in den entsprechenden gerichteten Graphen umgewandelt werden!

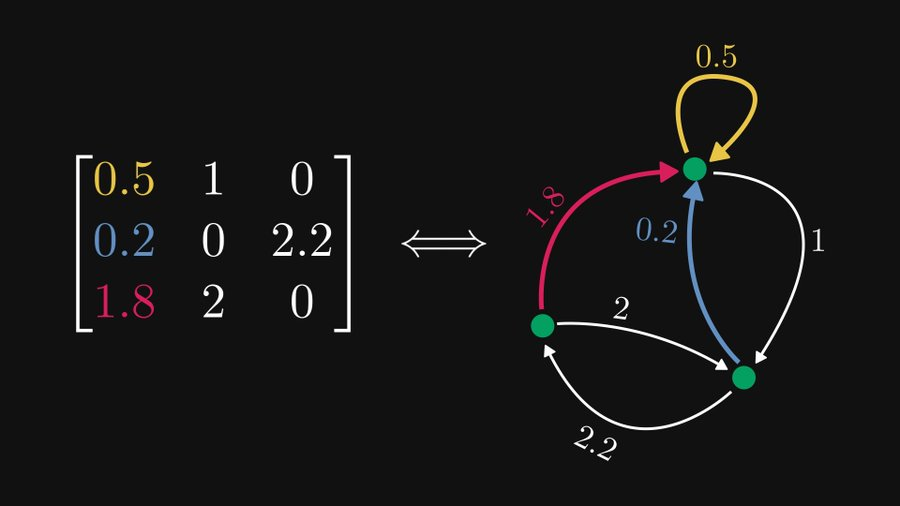
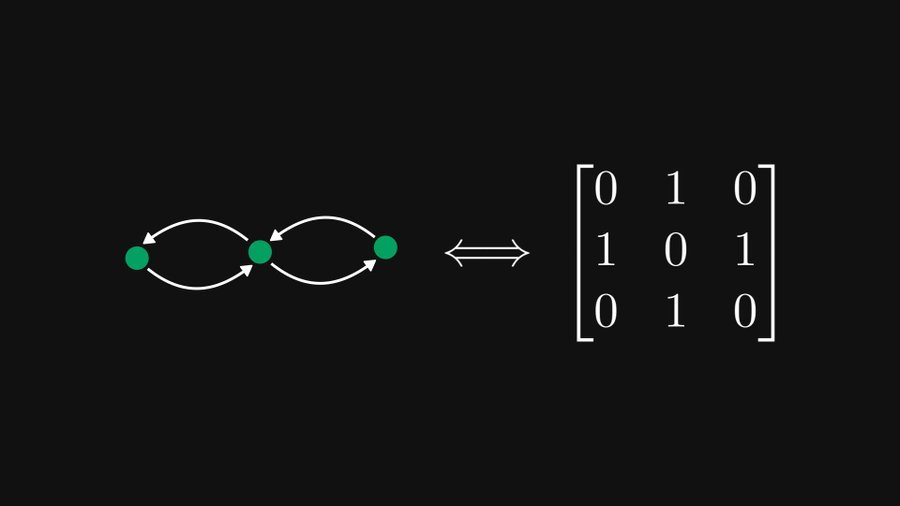
Wie in der Abbildung unten gezeigt, kann die 3×3-Matrix auf der linken Seite tatsächlich äquivalent als gerichteter Graph dargestellt werden, der rechts drei Knoten enthält, und diese Darstellung ist sowohl für die Matrix- als auch für die Graphentheorie sehr hilfreich.

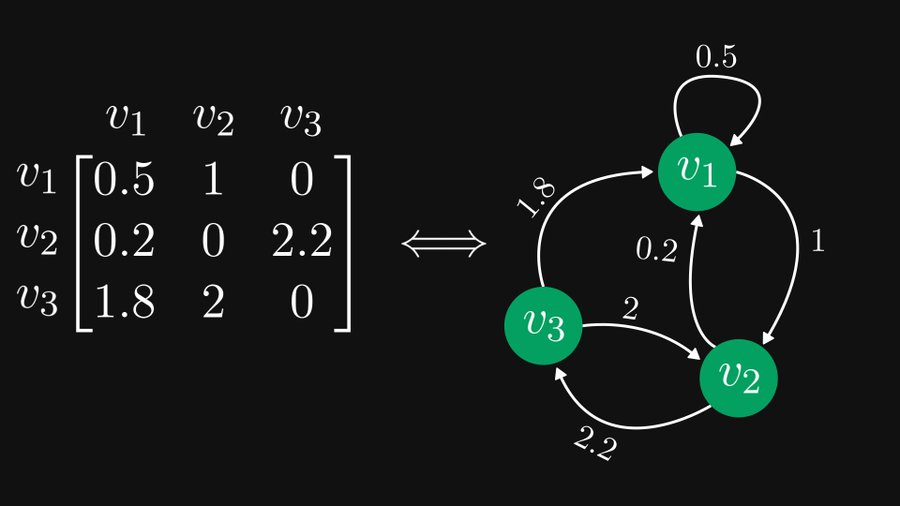
Dieses Beispiel stammt von Tivadar Danka, einem Mathematiker, der sich dafür einsetzt, Mathematik für alle zugänglich zu machen. Der selbsternannte „chaotisch gute“ Mathematiker stellte diese Äquivalenz von Matrizen und Graphen und deren Verwendung in einer Reihe von Tweets und Blogbeiträgen anschaulich vor. Bis heute wurden die Tweets mehr als 2 Millionen Mal gelesen, erhielten mehr als 3.200 Retweets und 9.100 Favoriten.

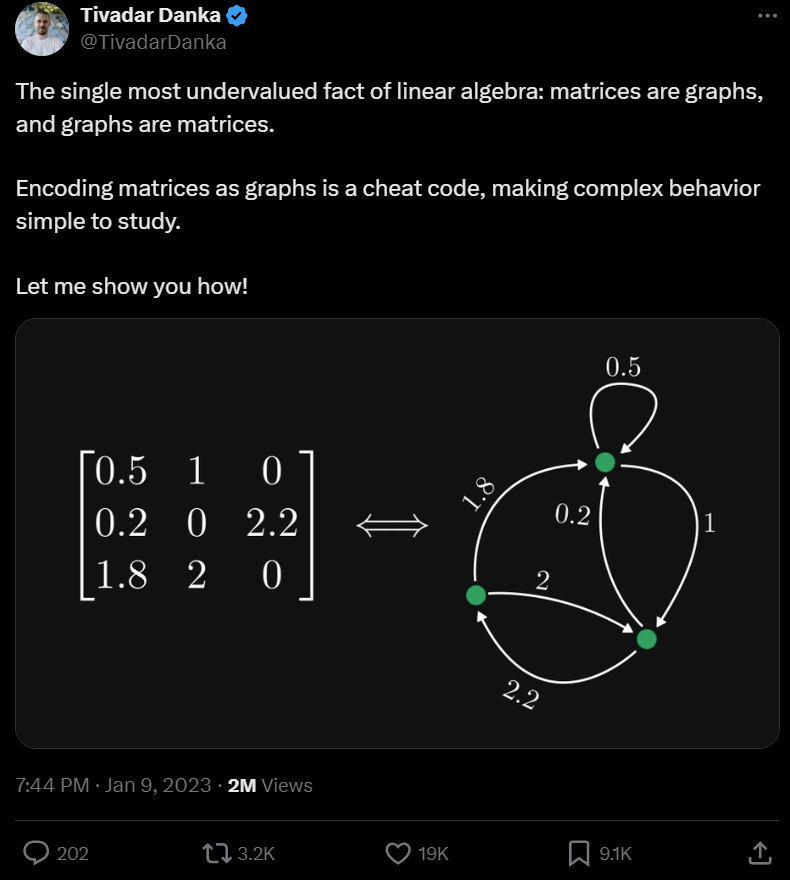
Die Wertigkeit von Matrizen und gerichteten Graphen

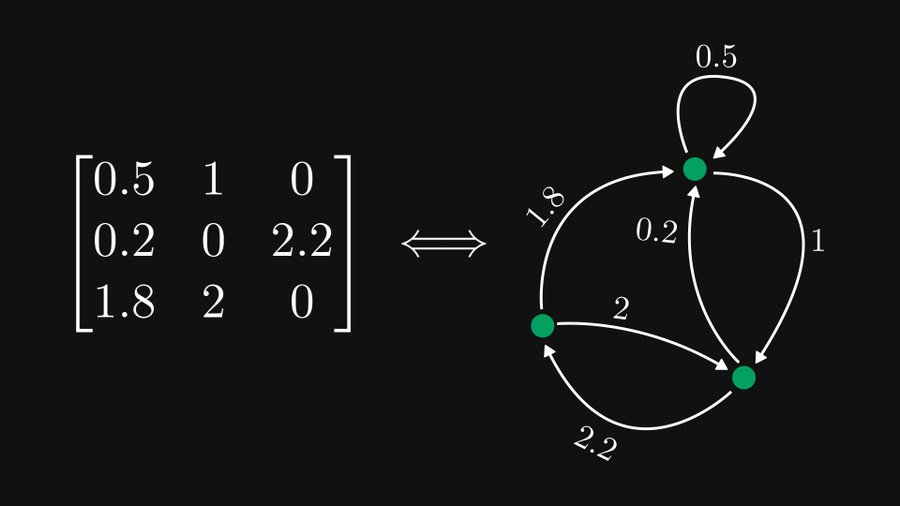
Wie im obigen Beispiel gezeigt, kann jedes Element als gerichtete und gewichtete Kanten dargestellt werden, wenn wir jede Zeile als Knoten behandeln. Natürlich können 0 Elemente ignoriert werden. Befindet sich das Element in Zeile i und Spalte j, entspricht es der Kante vom Knoten i zum Knoten j.

Das mag auf den ersten Blick kompliziert erscheinen, aber wir können uns zuerst einen der Knoten ansehen.

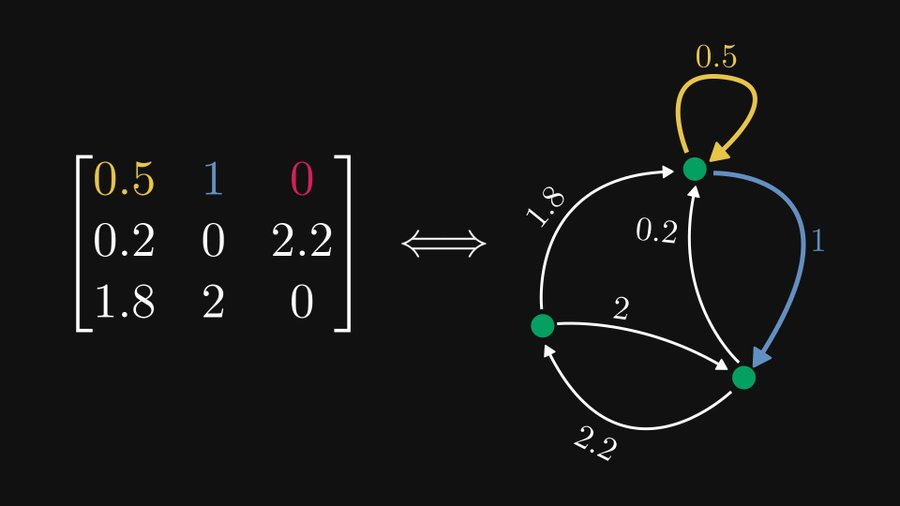
Wie in der Abbildung gezeigt, entspricht Zeile 1 für diese 3×3-Matrix dem obersten Knoten (wir nennen ihn hier Knoten 1), der 3 Elemente enthält, aber eines davon ist 0, also Dieser Knoten erweitert zwei Kanten. Die gelbe Kante stellt das Element 0,5 bei (1,1) dar, es handelt sich also um eine gerichtete Kante, die auf sich selbst zeigt und ein Gewicht von 0,5 hat. Ebenso ist die blaue Kante die Kante, die auf Knoten 2 zeigt und eine Gewichtung von 1 hat.

Auf diese Weise können wir analysieren, dass die i-te Spalte der Matrix allen Kanten entspricht, die auf den i-ten Knoten zeigen.

Was nützt dieser äquivalente Ausdruck?

Diese Äquivalenz zwischen nichtnegativen Matrizen und gerichteten Diagrammen kann uns nicht nur helfen, Matrizen und ihre Operationen besser zu verstehen, sondern auch dazu beitragen, einige Berechnungsprozesse zu vereinfachen. Dies kann uns auch dabei helfen, aus einer neuen Perspektive zu beginnen.

Zum Beispiel entspricht die Potenz der Matrix dem Gang im Diagramm.

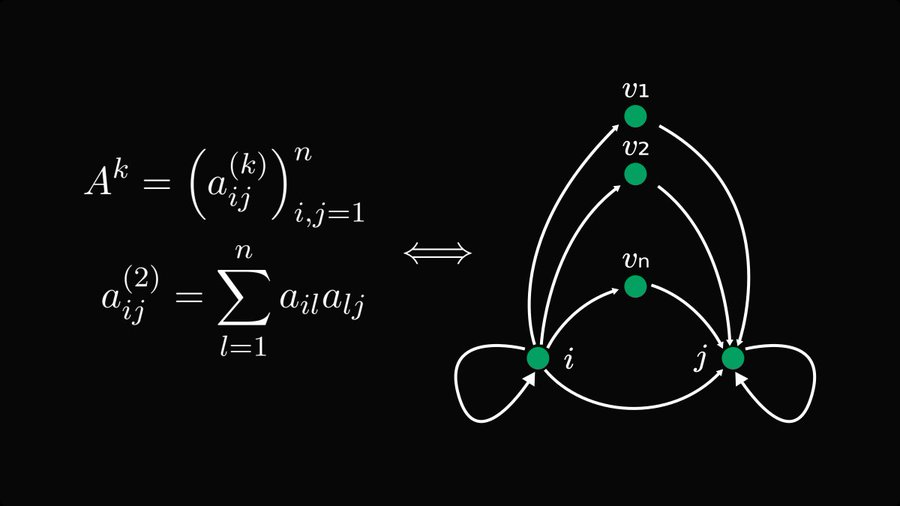
Wie in der Abbildung oben gezeigt, umfasst der Summierungsprozess jedes Elements für die k-te Potenz der n×n-Quadratmatrix A alle möglichen k-Schritt-Spaziergänge.

Angenommen, wir möchten das Quadrat der obigen 3×3-Matrix berechnen.

Wenn wir die Matrixmultiplikation verwenden, müssen wir sie wie folgt berechnen:

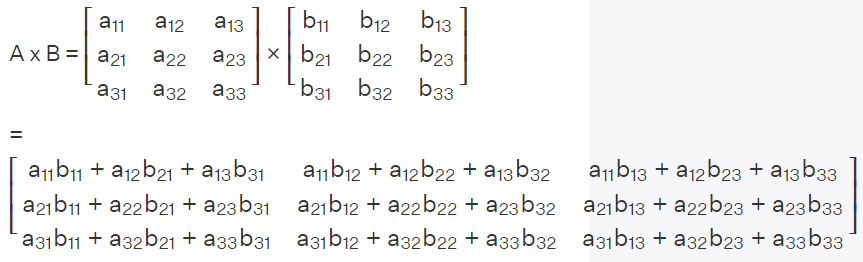
Für das erste Element des Operationsergebnisses können wir das Ergebnis = 0,5×0,5+1×0,2+0×1,8 erhalten = 0,45. Schließlich können wir das vollständige Ergebnis wie folgt erhalten:

Aber wenn wir die obige Graph-Walking-Methode verwenden, können wir das Ergebnis erhalten, indem wir den Pfad ablaufen. Ebenso müssen wir für das erste Element der Ergebnismatrix alle zweistufigen Gehwege aufsummieren, die a_{1,l}→a_{l,1} erfüllen.

Wenn dieser gerichtete Graph jedoch den Zustand einer Markov-Kette darstellt, stellt das Quadrat seiner Übergangswahrscheinlichkeitsmatrix im Wesentlichen die Wahrscheinlichkeit dar, dass die Kette nach zwei Schritten einen bestimmten Zustand erreicht.

Darüber hinaus kann die Verwendung von Diagrammen zur Darstellung von Matrizen uns auch ein tiefgreifendes Verständnis der Struktur nicht negativer Matrizen vermitteln. Um dies zu erreichen, müssen wir laut Danka zunächst das Konzept der „stark verbundenen Komponenten“ verstehen.

Stark verbundene Komponente

Was ist eine stark verbundene Komponente? Wenn bei einem gerichteten Graphen jeder andere Knoten im Graphen von jedem Knoten aus erreichbar ist, sagen wir, dass der Graph stark zusammenhängend ist. Wie unten gezeigt.

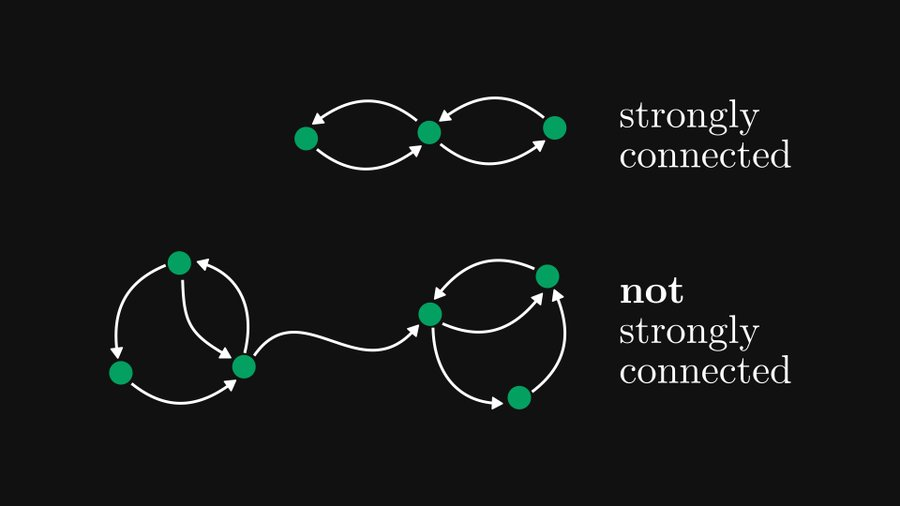
Die stark verbundene Komponente bezieht sich auf den Teil/Untergraphen im gerichteten Graphen, der eine starke Konnektivität erreichen kann. Wie in der Abbildung unten gezeigt, gibt es links und rechts eine stark verbundene Komponente, während der weiße Rand in der Mitte zu keiner stark verbundenen Komponente gehört.

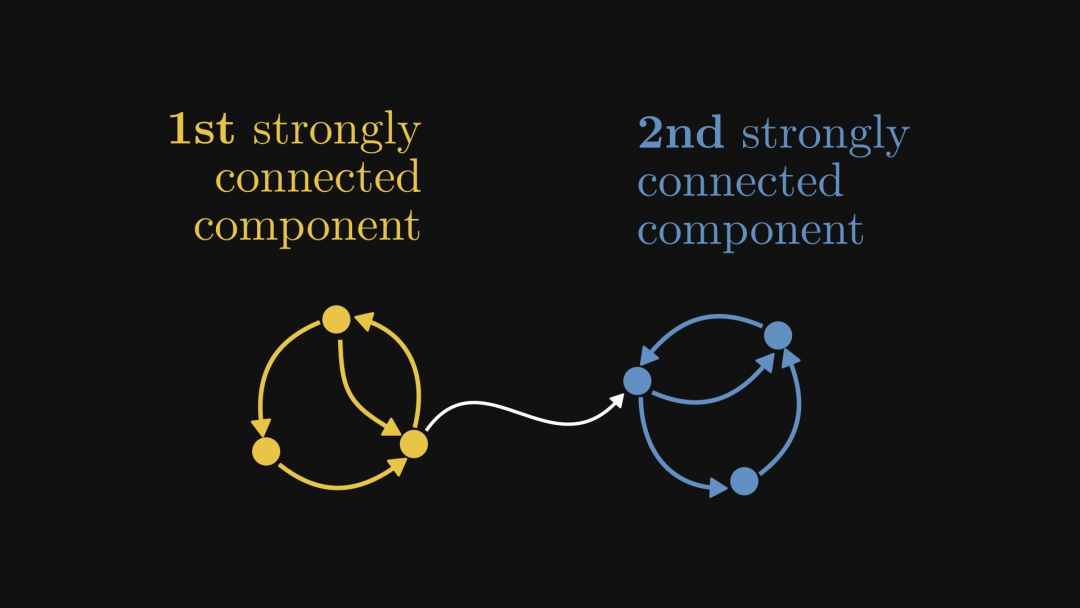
Die folgende Abbildung zeigt ein weiteres Beispiel, bei dem der gelbe Teil die stark verbundene Komponente ist:

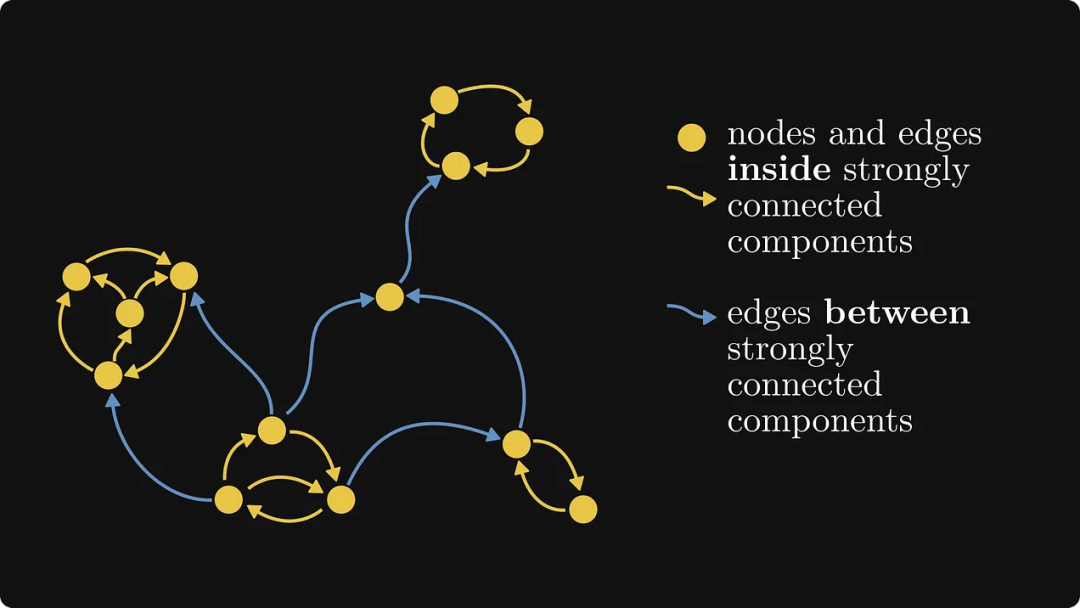
Die dem stark verbundenen Diagramm entsprechende Matrix ist eine irreduzible Matrix, während alle anderen Matrizen in der nichtnegativen Matrix enthalten sind sind reduzierbare Matrix.

Danka erklärt es anhand eines Beispiels. (Der Einfachheit halber sind alle Gewichte im Beispiel Einheitsgewichte, aber in der Praxis können diese Gewichtswerte alle nicht negativen Werte sein.)

Lassen Sie uns diesen Graphen transkribieren, der stark verbundene Komponenten enthält, aber nicht stark verbunden ist sich in die entsprechende Matrixform:

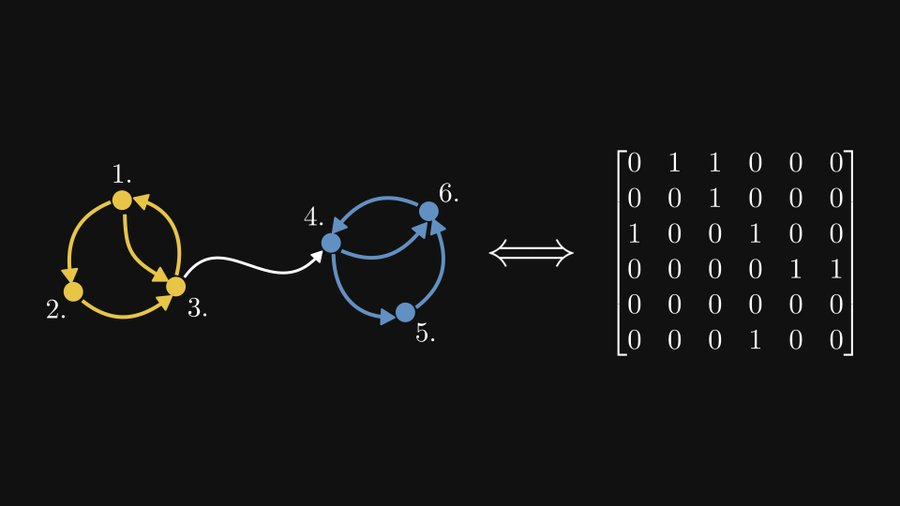
Und diese Matrix ist eine reduzierbare Matrix.

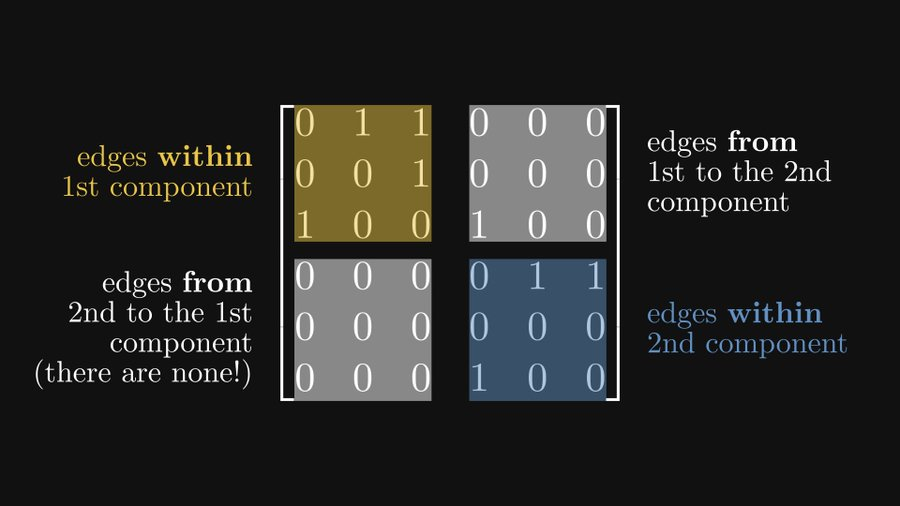
Es ist ersichtlich, dass die beiden Untermatrizen auf der Hauptdiagonale jeweils zwei stark verbundene Komponenten darstellen und die Untermatrix oben rechts die Kante von der ersten stark verbundenen Komponente zur zweiten stark verbundenen Komponente darstellt Unten links stellt die Kante von der zweiten stark verbundenen Komponente zur ersten stark verbundenen Komponente dar (da es keine solche Kante gibt, sind alle 0).

Diese Form des Schreibens einer Blockmatrix wird Frobenius-Normalform genannt.

Also fragen wir uns natürlich: Können wir jede nichtnegative Matrix in eine Frobenius-Normalformmatrix umwandeln?

Durch die Verwendung eines gerichteten Graphen zur Darstellung einer nicht negativen Matrix können wir leicht erkennen, dass die Antwort „Ja“ lautet, da jeder gerichtete Graph, der eine nicht negative Matrix darstellt, als stark verbundene Komponenten dargestellt werden kann, die miteinander verbunden sind. Dieser Vorgang ist sehr einfach:

1. Konstruieren Sie den entsprechenden gerichteten Graphen für die nichtnegative Matrix.

2. Finden Sie die stark verbundenen Komponenten.

3. Das ist es!

Verwenden Sie Bilder, um das Frobenius-Standardformular zu erhalten

Was ist also der bessere Weg? Anhand des obigen Beispiels werfen wir einen Blick auf den Prozess.

Verschmelzen Sie zunächst jede stark verbundene Komponente zu einem einzigen Objekt, wie in der Abbildung unten gezeigt. Zu diesem Zeitpunkt können wir jede stark verbundene Komponente als Black Box behandeln – wir kümmern uns nicht um ihre interne Struktur, sondern nur um ihre externen Verbindungen.

Dann müssen wir in diesem neuen Diagramm die Komponenten finden, die nur ausgehende Kanten, aber keine eingehenden Kanten haben. In diesem speziellen Beispiel gibt es nur eine, und wir beschriften sie mit der Nummer 0: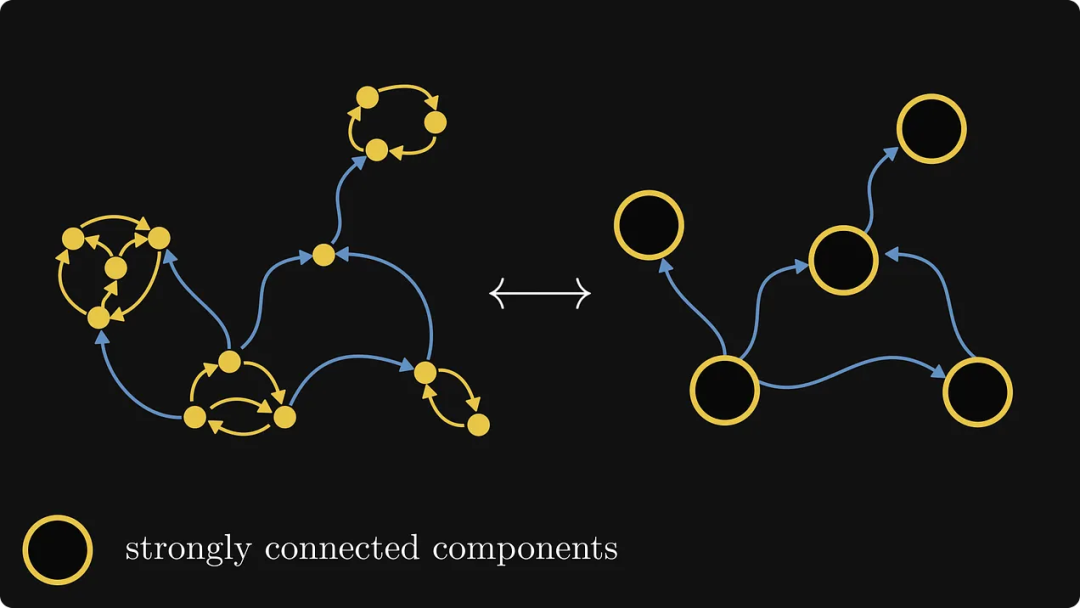

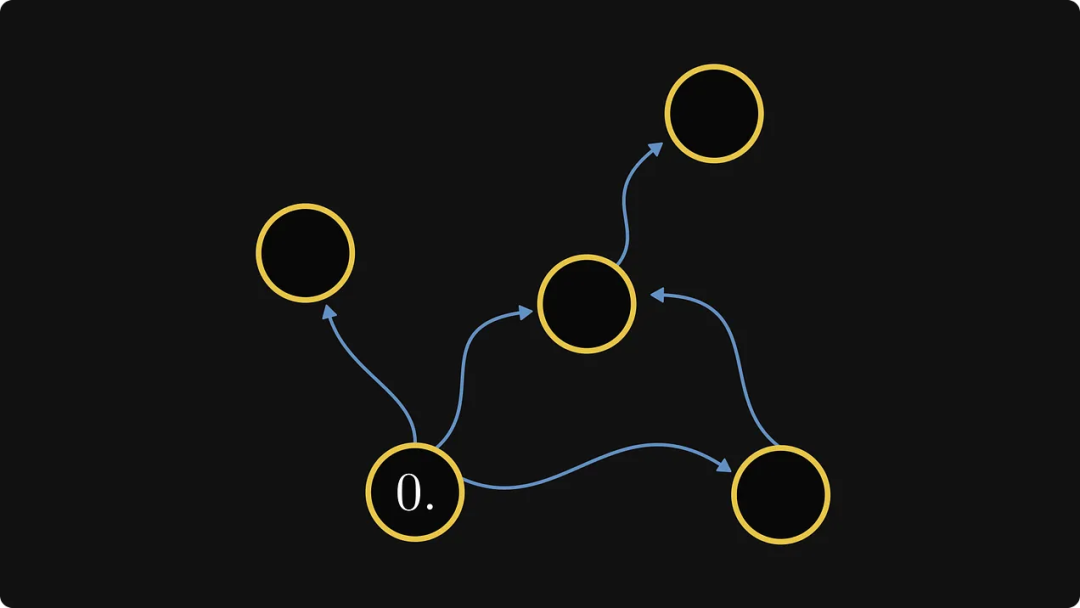
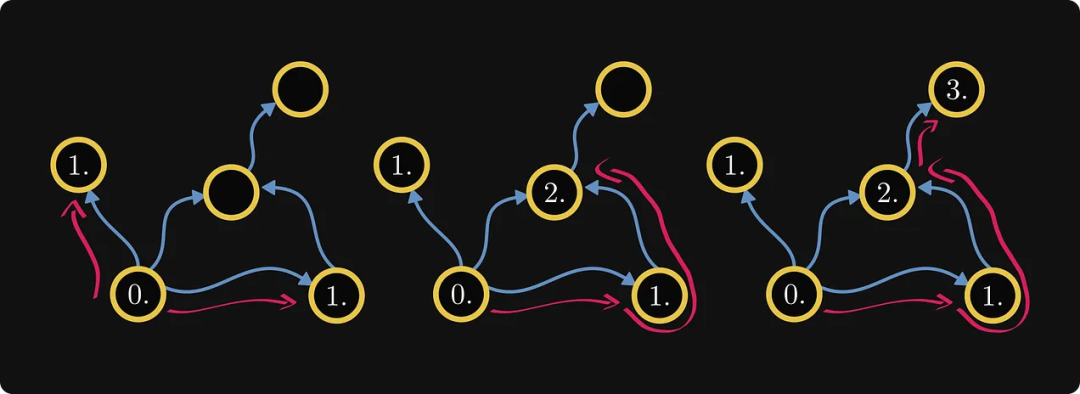
Der nächste Schritt ist schwieriger: Nummerieren Sie jede Komponente so, dass die Nummer jeder Komponente am weitesten von der Nummer 0 entfernt ist. Das folgende Beispiel kann diesen Punkt deutlicher veranschaulichen:

Sie können sehen, dass es zwei Pfade von Nr. 0 bis zur mittleren Komponente gibt. Wählen Sie daher den Pfad, der am weitesten von 0 entfernt ist, um ihn zu nummerieren. Endlich habe ich:

実際には、これはコンポーネントの順序を定義します。次に、各コンポーネントの内部ノードをマークします。

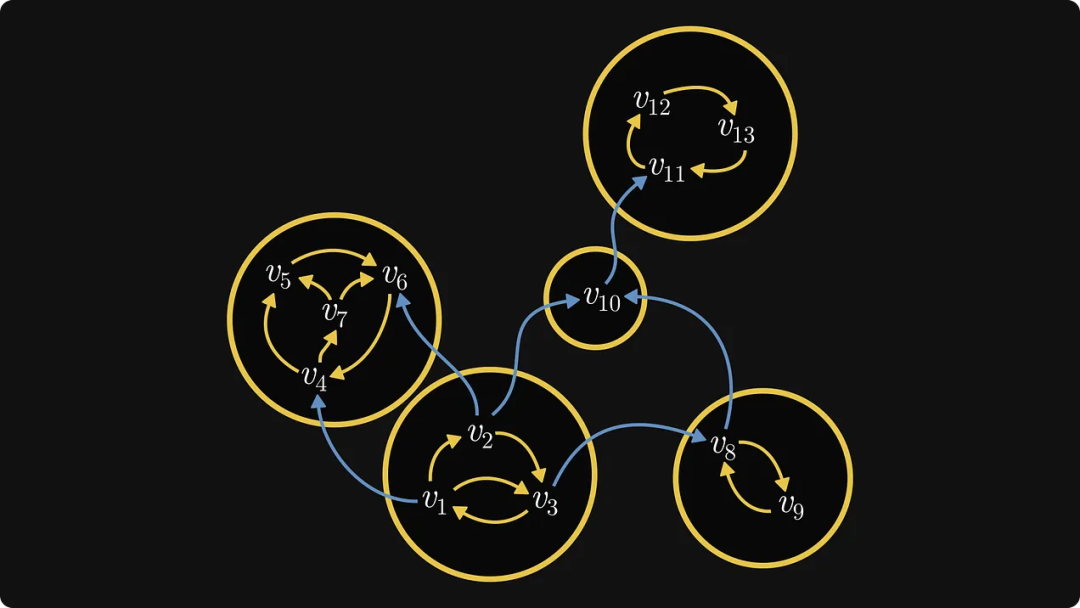
グラフ自体が行列からのものである場合、このような再ラベル付けプロセスにより Frobe が発生する可能性があります。 Nius正準形式マトリックス!

実際、この再ラベル付けプロセスは、置換行列 P を使用して元の行列を変換することであり、置換行列は次のように構成されます。複数の転置行列 積の構成。

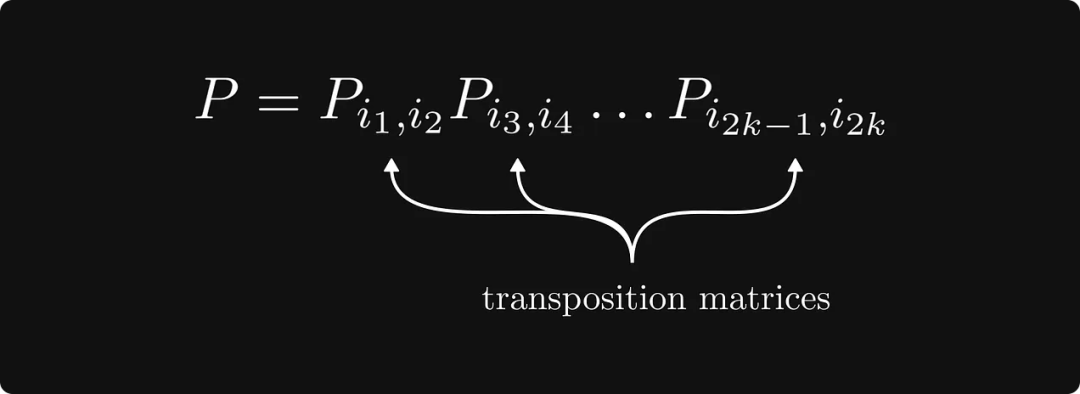
以下は定理の完全な形です:

もちろん、グラフを使用して行列を表す用途はこれをはるかに超えています。たとえば、行列の固有値を使用してグラフの固有値を定義することもできます。実際、この考え方からスペクトル グラフ理論という研究分野が生まれました。

結論

明らかに、行列とグラフの間のこの同値関係は、グラフ理論の研究に役立つだけでなく、線形代数にも役立ちます。計算と分析に対する新しい視点。たとえば、DNA データは行列やグラフの形式で表現されることがよくあります。

さらに、現在の大規模モデル AI にとって行列演算の重要性は誰もが知っており、ナレッジ グラフで表されるグラフも検索強化検索などの技術を通じて現在の AI の重要な推進力になりつつあります。この 2 つを接続すると、AI の解釈可能性とグラフ人工知能に新たなブレークスルーがもたらされる可能性があります。少なくとも、これは線形代数をより良く学ぶのに役立ちます。

実際、上記の内容は Tivadar Danka が執筆中の書籍「Mathematics of Machine Learning」から抜粋したものです。本書は、機械学習に関連する数学的知識を簡単なレベルから深いレベルまで紹介しており、読者が何が起こっているのか、なぜそうなのかを真に理解できるようにするものであり、ダンカ氏は「機械学習を学ぶための最良のリソース」であると自信を持って断言します。現在、彼は 2 つの章のプレビューをオンラインで公開しています。興味のある読者は https://tivadardanka.com/mathematics-of-machine-learning-preview/

にアクセスしてください。

Das obige ist der detaillierte Inhalt vonWarum wusste ich beim Erlernen der Liniengenerierung nicht: Es gibt eine Äquivalenzbeziehung zwischen Matrizen und Graphen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!