Wird spekulatives Sampling die Inferenzgenauigkeit großer Sprachmodelle verlieren?

Mitchell Stern und andere schlugen 2018 das Prototyp-Konzept des spekulativen Samplings vor. Dieser Ansatz wurde seitdem durch verschiedene Arbeiten weiterentwickelt und verfeinert, darunter Lookahead Decoding, REST, Medusa und EAGLE, wo spekulatives Sampling den Inferenzprozess großer Sprachmodelle (LLMs) erheblich beschleunigt.

Eine wichtige Frage ist: Beeinträchtigt spekulatives Sampling im LLM die Genauigkeit des Originalmodells? Lassen Sie mich mit der Antwort beginnen: Nein.

Der standardmäßige spekulative Stichprobenalgorithmus ist verlustfrei, und dieser Artikel wird dies durch mathematische Analysen und Experimente beweisen.

Mathematischer Beweis

Die spekulative Stichprobenformel kann wie folgt definiert werden:

wobei:

• ? eine reelle Zahl ist, die aus einer gleichmäßigen Verteilung entnommen wurde.
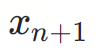• ist der nächste vorherzusagende Token.
• ?(?) ist die nächste Token-Verteilung, die vom Entwurfsmodell vorgegeben wird.
• ?(?) ist die nächste Tokenverteilung, die vom Basismodell vorgegeben wird.

Der Einfachheit halber lassen wir die Wahrscheinlichkeitsbedingung weg. Tatsächlich sind ? und ? bedingte Verteilungen, die auf der Präfix-Token-Sequenz basieren .

Das Folgende ist der Beweis für die Verlustlosigkeit dieser Formel im DeepMind-Papier:

Wenn Ihnen das Lesen mathematischer Gleichungen zu langweilig ist, veranschaulichen wir als Nächstes den Beweisprozess anhand einiger intuitiver Diagramme.

Dies ist das Verteilungsdiagramm des Entwurfsmodells ? und des Basismodells ?:

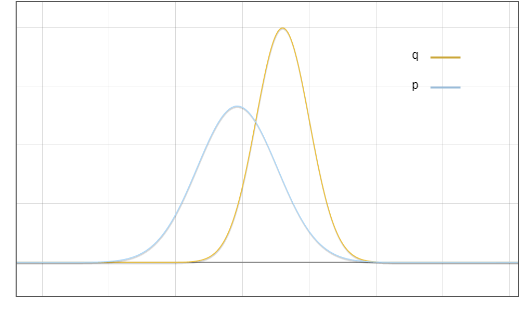
Abbildung 1: Die Wahrscheinlichkeitsdichtefunktion der Ausgabeverteilung des Entwurfsmodells p und des Basismodells q

Es sollte beachtet werden dass dies nur ein idealisiertes Diagramm ist. In der Praxis berechnen wir eine diskrete Verteilung, die wie folgt aussieht:

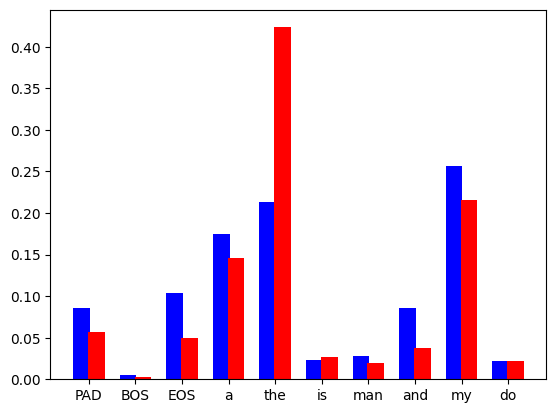
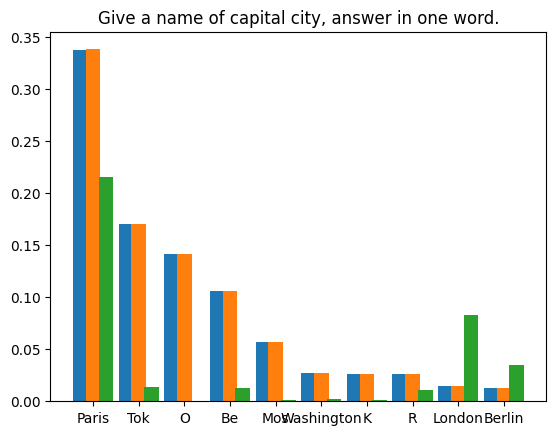
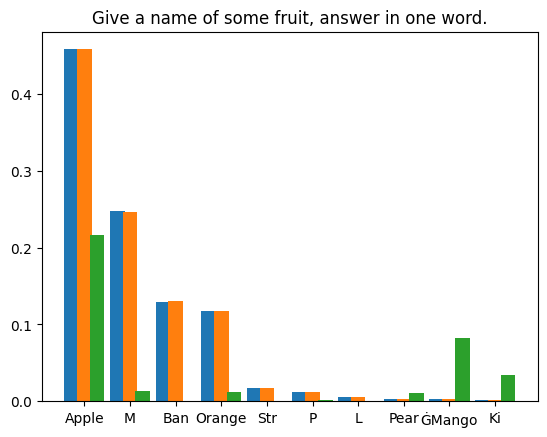
Abbildung 2: Das Sprachmodell sagt die diskrete Wahrscheinlichkeitsverteilung jedes Tokens im Vokabularsatz voraus, der blaue Balken stammt aus dem Entwurfsmodell und Der rote Balken stammt vom Basismodell.

Der Einfachheit und Klarheit halber diskutieren wir dieses Problem jedoch anhand seiner kontinuierlichen Approximation.

Die Frage ist nun: Wir nehmen eine Probe aus der Verteilung, aber wir möchten, dass das Endergebnis so ist, wie wir es genommen haben. Eine Schlüsselidee ist: Verschieben Sie die Wahrscheinlichkeit des roten Bereichs in den gelben Bereich:

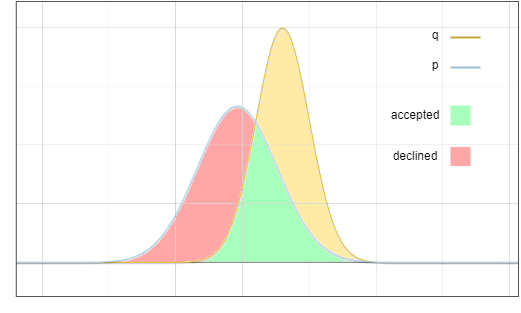
Abbildung 3: Akzeptanz- und Ablehnungsstichprobenbereich

Zielverteilung? Kann als Summe zweier Teile angesehen werden:

I Akzeptanz

In diesem Zweig gibt es zwei unabhängige Ereignisse:

1. Bei der Stichprobenverteilung wird ein bestimmtes Token erzeugt?. Die Wahrscheinlichkeit ist ?(?)
2. Zufallsvariable ?Akzeptiere das Token ?. Die Wahrscheinlichkeiten sind:

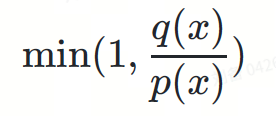
Multiplizieren Sie diese Wahrscheinlichkeiten: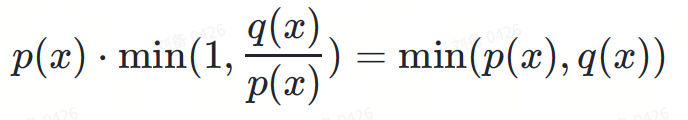

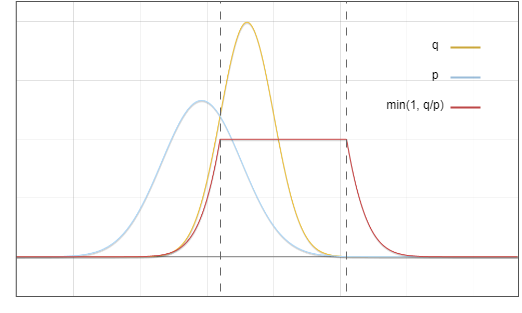
Abbildung 4: Multiplizieren Sie die blauen und roten Linien. Das Ergebnis ist die grüne Linie in Abbildung 6

II. Validierungsablehnung

in diesem Zweig auch zwei unabhängige Ereignisse:

1. ? weist einen bestimmten Token in ? zurück, die Wahrscheinlichkeit ist:

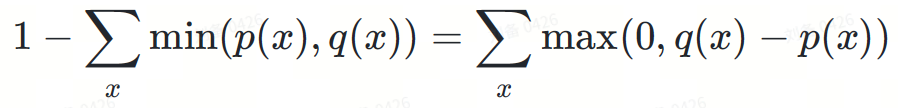
Dies ist ein ganzzahliger Wert, der Wert hat nichts mit dem spezifischen Token x zu tun

1. ist eine positive Zahl in Verteilung ?−?(Teilweises) Upsampling generiert ein bestimmtes Token?, die Wahrscheinlichkeit ist:

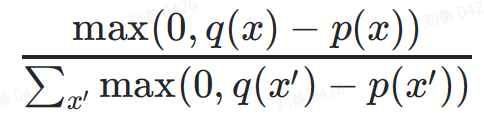
Die Funktion seines Nenners besteht darin, die Wahrscheinlichkeitsverteilung zu normalisieren, um das Wahrscheinlichkeitsdichteintegral gleich 1 zu halten.

Zwei Elemente werden miteinander multipliziert und der Nenner des zweiten Termes eliminiert:

max(0,?(?)−?(?))

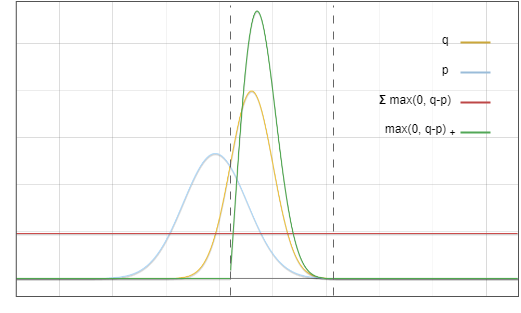
Abbildung 5. Die entsprechenden Funktionen der roten Linie und grüne Linie in dieser Abbildung Zusammen multipliziert entspricht das Ergebnis der roten Linie in Abbildung 6

Warum wird die Ablehnungswahrscheinlichkeit zufällig auf max(0,?−?) normiert? Auch wenn es wie ein Zufall erscheinen mag, ist hier eine wichtige Beobachtung, dass die Fläche des roten Bereichs in Abbildung 3 gleich der Fläche des gelben Bereichs ist, da das Integral aller Wahrscheinlichkeitsdichtefunktionen gleich 1 ist.

Fügen Sie die beiden Teile I und II hinzu: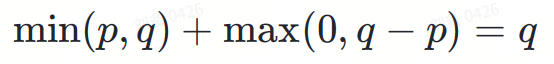

Schließlich erhalten wir die Zielverteilung?.

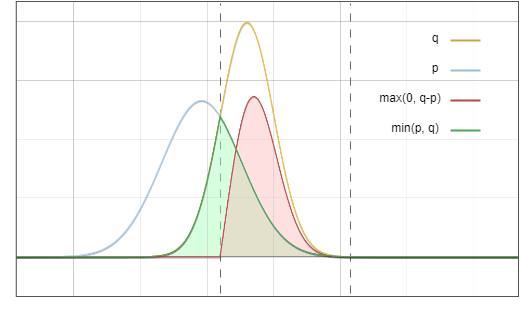
Abbildung 6. Die Summe der grünen Fläche und der roten Fläche entspricht genau der Fläche unterhalb der gelben Linie

Und das ist unser Ziel.

Experimente

Obwohl wir im Prinzip bewiesen haben, dass spekulatives Sampling verlustfrei ist, kann es dennoch zu Fehlern bei der Implementierung des Algorithmus kommen. Daher ist auch eine experimentelle Überprüfung erforderlich.

Wir haben Experimente in zwei Fällen durchgeführt: der deterministischen Methode der gierigen Dekodierung und der stochastischen Methode der polynomialen Stichprobenziehung.

Greedy Decoding

Wir bitten LLM, Kurzgeschichten zweimal zu generieren, zunächst mit gewöhnlicher Inferenz und dann mit spekulativem Sampling. Die Probenahmetemperatur wird für beide Zeiten auf 0 eingestellt. Wir haben die spekulative Sampling-Implementierung in Medusa verwendet. Das Modellgewicht ist medusa-1.0-vicuna-7b-v1.5 und das Basismodell vicuna-7b-v1.5.

Nach Abschluss des Testlaufs kamen wir zu zwei exakt gleichen Ergebnissen. Der generierte Text lautet wie folgt:

und EAGLE-LLaMA3-Instruct-8B. Die statistischen Ergebnisse lauten wie folgt:

Benutzer: Bitte erzählen Sie eine Geschichte über einen Cyperpunk-Ritter namens PPIO, der ein bezauberndes Lama als Haustier hält.

Assistent: Es war einmal, in einer Welt, in der Die Technologie war über unsere kühnsten Träume hinaus fortgeschritten, da lebte ein Cyberpunk-Ritter namens PPIO. PPIO war ein erfahrener Krieger mit fortschrittlichen kybernetischen Verbesserungen, die ihm unglaubliche Kraft und Geschwindigkeit verliehen. Er war auch ein Mann von großer Ehre, der immer danach strebte, das Richtige zu tun Und einfach .

Eines Tages stieß PPIO auf einer Mission auf ein wunderschönes Lama. Obwohl PPIO ein kybernetisches Wesen war, hatte er eine Schwäche für Tiere und konnte nicht widerstehen, das Lama vor der Gefahr zu retten, die es auch gewesen sein mochte Von diesem Tag an folgte das Lama PPIO, wohin er auch ging, und die beiden wurden schnelle Freunde.

Das Lama, dessen Name Llama-ella war, war ein besonderes Lama. Es hatte eine einzigartige Fähigkeit zu spüren, wenn jemand da war PPIO war dankbar für Llama-ellas Fähigkeiten und die beiden wurden ein unaufhaltsames Team. Gemeinsam nahmen PPIO und Llama-ella alle möglichen Herausforderungen an Sie kämpften gegen kybernetische Bösewichte, um unschuldige Menschen vor Schaden zu bewahren, und ihr Mut und ihre Ehre waren eine Inspiration für alle, die sie kannten , Die Situation ist komplizierter. Die meisten Methoden zur Reproduktion von Ergebnissen in randomisierten Programmen verwenden feste Zufallsstartwerte, um den Determinismus von Pseudozufallsgeneratoren auszunutzen. Dieser Ansatz ist jedoch für unser Szenario nicht geeignet. Unser Experiment basiert auf dem Gesetz der großen Zahlen: Bei genügend Stichproben konvergiert der Fehler zwischen der tatsächlichen Verteilung und der theoretischen Verteilung gegen Null.

Wir haben vier Eingabeaufforderungstexte zusammengestellt und 1.000.000 spekulative Stichprobeniterationen für den ersten von LLM unter jeder Eingabeaufforderung generierten Token durchgeführt. Die verwendeten Modellgewichte sind

Llama3 8B Instruct

• Blue: softmax from base model output logits
• Green: softmax from draft model output logitsOrange: from cast Machine sampling (1,000,000 times) The first token count proportion of
• The standard deviation between the basic model output result and the sampling distribution is 9.694e-5. As expected.

Conclusion

Speculative sampling does not harm the inference accuracy of large language models. Through rigorous mathematical analysis and practical experiments, we demonstrate the lossless nature of the standard speculative sampling algorithm. The mathematical proof shows how the speculative sampling formula preserves the original distribution of the underlying model. Our experiments, including deterministic greedy decoding and probabilistic polynomial sampling, further validate these theoretical findings. The greedy decoding experiment produced the same results with and without speculative sampling, while the polynomial sampling experiment showed that the difference in token distribution is negligible across a large number of samples.

Together, these results demonstrate that speculative sampling can significantly speed up LLM inference without sacrificing accuracy, paving the way for more efficient and accessible AI systems in the future.

Das obige ist der detaillierte Inhalt vonWird spekulatives Sampling die Inferenzgenauigkeit großer Sprachmodelle verlieren?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!