Training mit Millionen von Kristalldaten zur Lösung kristallographischer Phasenprobleme, die Deep-Learning-Methode PhAI wird in Science veröffentlicht

Herausgeber |. KX

Bis heute sind die durch die Kristallographie ermittelten Strukturdetails und Präzision, von einfachen Metallen bis hin zu großen Membranproteinen, mit keiner anderen Methode zu erreichen. Die größte Herausforderung, das sogenannte Phasenproblem, bleibt jedoch die Gewinnung von Phaseninformationen aus experimentell bestimmten Amplituden.

Forscher der Universität Kopenhagen, Dänemark, haben eine Deep-Learning-Methode namens PhAI entwickelt, um Kristallphasenprobleme zu lösen. Ein Deep-Learning-Neuronales Netzwerk, das mit Millionen künstlicher Kristallstrukturen und den entsprechenden synthetischen Beugungsdaten trainiert wird, kann genaue Elektronendichtekarten erstellen. .

Untersuchungen zeigen, dass diese auf Deep Learning basierende Ab-initio-Strukturlösungsmethode das Phasenproblem mit einer Auflösung von nur 2 Angström lösen kann, was nur 10 % bis 20 % der verfügbaren Daten bei atomarer Auflösung entspricht, während herkömmliche Ab-initio Methoden erfordern typischerweise eine atomare Auflösung.

Relevante Forschung trug den Titel „PhAI: Ein Deep-Learning-Ansatz zur Lösung des kristallographischen Phasenproblems“ und wurde am 1. August in „Science“ veröffentlicht.

Link zum Papier: https://www.science.org/doi/10.1126/science.adn2777

Kristallographie ist eine der zentralen Analysetechniken in den Naturwissenschaften. Die Röntgenkristallographie ermöglicht einen einzigartigen Einblick in die dreidimensionale Struktur von Kristallen.

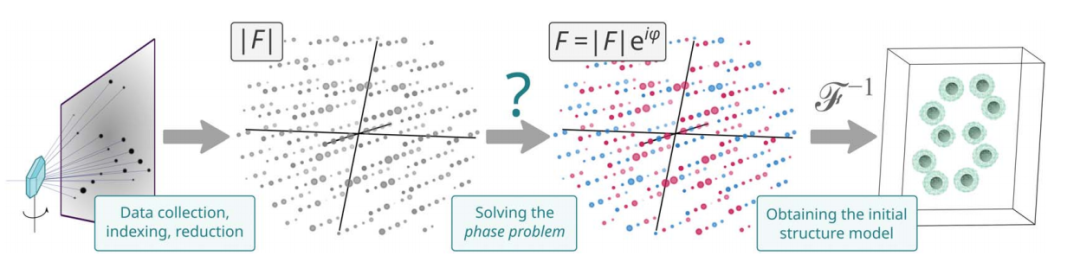
Um die Elektronendichtekarte zu rekonstruieren, müssen genügend komplexe Strukturfaktoren $F$ der Beugungsreflexe bekannt sein. In einem herkömmlichen Experiment wird nur die Amplitude $|F|$ erhalten, während die Phase $phi$ verloren geht. Dies ist ein kristallographisches Phasenproblem.

Abbildung: Standard-Flussdiagramm zur Bestimmung der Kristallstruktur. (Quelle: Paper)

Ein großer Durchbruch gelang in den 1950er und 1960er Jahren, als Karle und Hauptmann** sogenannte direkte Methoden zur Lösung von Phasenproblemen entwickelten. Die direkte Methode erfordert jedoch Beugungsdaten mit atomarer Auflösung. Das Erfordernis einer atomaren Auflösung ist jedoch eine empirische Beobachtung.

In den letzten Jahren wurden traditionelle direkte Methoden durch Dual-Space-Methoden ergänzt. Die derzeit verfügbaren Ab-initio-Methoden scheinen an ihre Grenzen gestoßen zu sein. Eine allgemeine Lösung des Phasenproblems bleibt unbekannt.

Mathematisch gesehen kann jede Kombination aus Strukturfaktoramplitude und -phase einer inversen Fourier-Transformation unterzogen werden. Physikalische und chemische Anforderungen (z. B. eine atomarähnliche Elektronendichteverteilung) legen jedoch Regeln für die möglichen Kombinationen von Phasen fest, die mit einer Reihe von Amplituden übereinstimmen. Fortschritte im Deep Learning ermöglichen es, diesen Zusammenhang zu untersuchen, möglicherweise tiefergehend als mit den aktuellen Ab-initio-Methoden.

Hier haben Forscher der Universität Kopenhagen einen datengesteuerten Ansatz gewählt und Millionen künstlicher Kristallstrukturen und deren entsprechende Beugungsdaten verwendet, um Phasenprobleme in der Kristallographie zu lösen.

Studie zeigt, dass diese auf Deep Learning basierende Ab-initio-Strukturlösungsmethode mit einer Auflösung von nur minimalem Gitterebenenabstand (dmin) = 2,0 Å durchgeführt werden kann, wobei nur die für die direkte Methode erforderlichen Daten verwendet werden (10 % bis 20 %). .

Neuronales Netzwerkdesign und Training

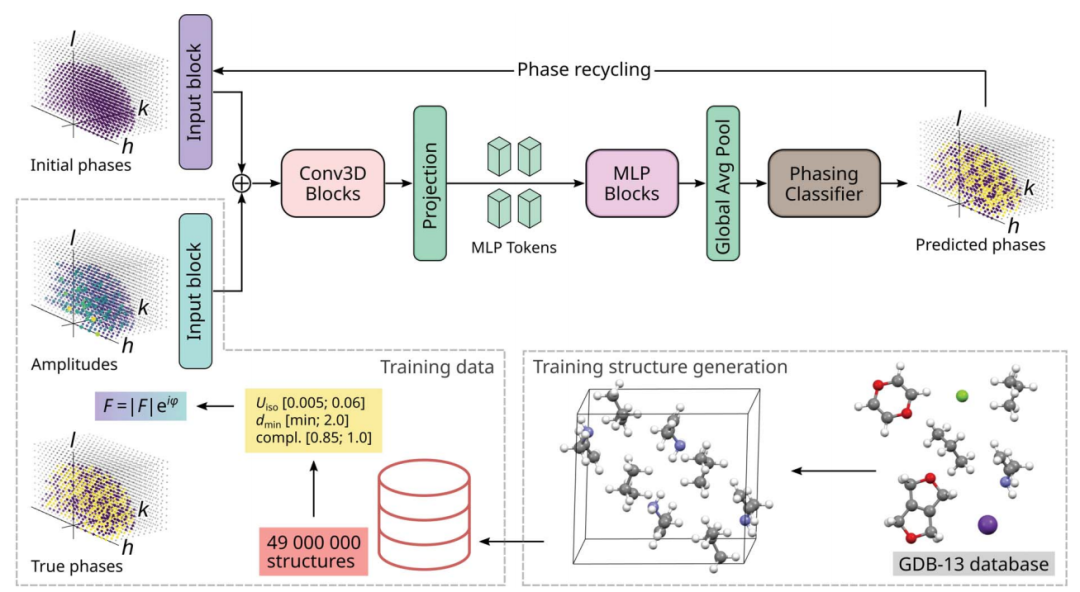
Das konstruierte künstliche neuronale Netzwerk heißt PhAI, das die Strukturfaktoramplitude |F| akzeptiert und den entsprechenden Phasenwert ϕ ausgibt. Die Architektur von PhAI ist in der folgenden Abbildung dargestellt.

Abbildung: Die neuronale Netzwerkmethode PhAI löst das Phasenproblem. (Quelle: Paper) Die Anzahl der Strukturfaktoren in einer Kristallstruktur hängt von der Elementarzellengröße ab. Abhängig von den Rechenressourcen sind der Größe der Eingabedaten Grenzen gesetzt. Die Amplituden der Eingabestrukturfaktoren werden auf der Grundlage der Miller-Indizes (h, k, l) gemäß der

1-Reflexion ausgewählt.
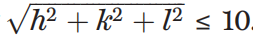
Das heißt, Strukturen, die bei atomarer Auflösung auf Elementarzellenabmessungen von etwa 10 Å beschränkt sind. Darüber hinaus wurde die häufigste zentrosymmetrische Raumgruppe P21/c gewählt. Die zentrale Symmetrie begrenzt die möglichen Phasenwerte auf Null oder π rad.

2. 主に有機分子を含む人工結晶構造を用いたニューラルネットワークの学習に関する研究。約 4,900 万個の構造が作成され、そのうち 94.29% が有機結晶構造、5.66% が金属有機結晶構造、0.05% が無機結晶構造でした。
3. ニューラル ネットワークへの入力は振幅と位相で構成され、畳み込み入力ブロックによって処理され、一連の畳み込みブロック (Conv3D) に追加されて供給され、その後に一連の多層パーセプトロン (MLP) ブロックが続きます。線形分類器（位相分類器）からの予測位相は、ネットワークを Nc 回循環します。トレーニング データは、GDB-13 データベースからの金属原子と有機分子を単位セルに挿入することによって生成されました。得られた構造はトレーニング データに編成され、そこからサンプリングされた温度係数での真の位相と構造係数の振幅、分解能、完全性を計算できます。
   実際の構造問題を解決する
4. トレーニングされたニューラル ネットワークは、中程度の計算要件を持つ標準的なコンピューター上で実行されます。 hkl インデックスと対応する構造因子振幅のリストを入力として受け入れます。他の入力情報は必要なく、構造の単位セル パラメーターも必要ありません。これは、他のすべての現代の ab initio メソッドとは根本的に異なります。ネットワークは、その場で位相値を予測して出力できます。
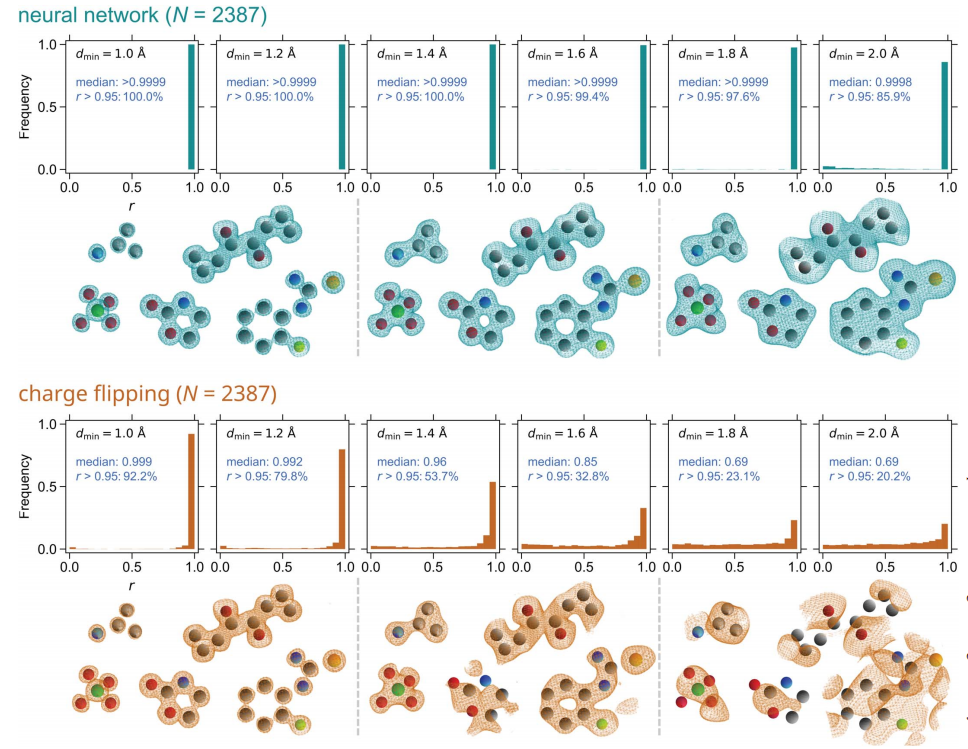
5. 研究者らは、実際の結晶構造から計算された回折データを使用してニューラル ネットワークのパフォーマンスをテストしました。合計 2387 のテスト ケースが取得されました。収集されたすべての構造について、1.0 ～ 2.0 Å の範囲の複数のデータ解像度値が考慮されました。比較のために、チャージフリップ法も位相情報の取得に使用されました。

   

   イラスト: 位相と真の電子密度マップ間の相関係数 r のヒストグラム。
   (出典: 論文)

トレーニングされたニューラル ネットワークは良好なパフォーマンスを発揮します 対応する回折データの解像度が高ければ、テストされたすべての構造 (N = 2387) を解くことができ、低解像度の構造を解くのに優れています。データ 優れたパフォーマンス。ニューラル ネットワークが無機構造に対してトレーニングされることはほとんどありませんが、そのような構造を完全に解決できます。

電荷フリップ法は、高解像度データを処理する場合には良好に機能しますが、データ解像度が低下するにつれて、適切に正しい解を生成する能力は徐々に低下しますが、それでも 1.6 Å % 構造の解像度で約 32 ピクセルを解決します。電荷反転によって特定される構造の数は、さらなる実験と反転閾値などの入力パラメータの変更によって改善できます。

PhAI アプローチでは、このメタ最適化はトレーニング中に実行され、ユーザーが実行する必要はありません。これらの結果は、位相を最初から計算するには原子分解能データが必要であるという結晶学における一般的な概念が崩れている可能性があることを示唆しています。 PhAI は 10% ～ 20% の原子分解能データのみを必要とします。

この結果は、原子分解能が ab initio 法には必要なく、深層学習ベースの構造決定に新しい道を開くことを明確に示しています。この深層学習アプローチの課題

は、ニューラル ネットワークをスケールすることです。つまり、より大きな単位セルの回折データには、トレーニング中に大量の入出力データと計算コストが必要になります。将来的には、この方法を一般的なケースに拡張するには、さらなる研究が必要です。

Das obige ist der detaillierte Inhalt vonTraining mit Millionen von Kristalldaten zur Lösung kristallographischer Phasenprobleme, die Deep-Learning-Methode PhAI wird in Science veröffentlicht. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!