
Die AIxiv-Kolumne ist eine Kolumne, in der diese Website akademische und technische Inhalte veröffentlicht. In den letzten Jahren sind in der AIxiv-Kolumne dieser Website mehr als 2.000 Berichte eingegangen, die Spitzenlabore großer Universitäten und Unternehmen auf der ganzen Welt abdecken und so den akademischen Austausch und die Verbreitung wirksam fördern. Wenn Sie hervorragende Arbeiten haben, die Sie teilen möchten, können Sie gerne einen Beitrag leisten oder uns für die Berichterstattung kontaktieren. E-Mail-Adresse: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
Die Autoren dieses Artikels sind Zhang Junpeng, Ren Qihan und Zhang Quanshi. Unter ihnen ist Zhang Junpeng ein angehender Doktorand von Zhang Quanshi und Ren Qihan ist ein Doktorand von Zhang Quanshi. In diesem Artikel wird zunächst kurz das „Theoretische System der äquivalenten Interaktionsinterpretabilität“ (20 CCF-A- und ICLR-Artikel) besprochen und auf dieser Grundlage die Leistung neuronaler Netze in der Dynamik genau abgeleitet und vorhergesagt Änderungen seiner konzeptionellen Darstellung und seiner Verallgemeinerung während des Trainingsprozesses, das heißt, wir können bis zu einem gewissen Grad die Verallgemeinerung des neuronalen Netzwerks zu jedem Zeitpunkt während des Trainingsprozesses und seine internen Ursachen erklären. Unser Team hat lange über eine ultimative Frage im Bereich der Interpretierbarkeit nachgedacht, nämlich
Was ist das erste Prinzip im Bereich der Interpretierbarkeit? ? Für die sogenannten ersten Prinzipien gibt es derzeit keinen allgemein akzeptierten Rahmen. Es gibt keine Möglichkeit, einen solchen Weg schrittweise zu definieren. Wir müssen eine große Anzahl axiomatischer Anforderungen in einem neuen theoretischen System aufstellen und eine Theorie entwickeln, die den inneren Mechanismus neuronaler Netze aus verschiedenen Blickwinkeln genau und genau erklären kann. Ein theoretisches System, das alle Aspekte neuronaler Netze genau erklären kann, wird als „erste Prinzipien“ bezeichnet. Wenn Sie „Wissenschaft“ wirklich konsequent betreiben, dann darf das erste Prinzip nicht so einfach sein wie gedacht, sondern ein komplexes System, das Forschung und Berücksichtigung aller Aspekte des Deep Learning erfordert. Wenn Sie subjektiv nicht dazu bereit sind oder nicht glauben, dass eine Theorie streng genug sein muss, wird die Forschung natürlich um ein Vielfaches einfacher. Genauso wie das Standardmodell der Physik komplizierter sein muss als die Newtonschen Gesetze, je nachdem, welchen Weg man einschlagen möchte.
In dieser Richtung hat unser Team das „
Equivalent Interactive Interpretability Theoretical System“ unabhängig von Grund auf konstruiert und auf der Grundlage dieser Theorie den intrinsischen Mechanismus neuronaler Netze aus drei Perspektiven erklärt.
1. Theoretische Grundlage der semantischen Erklärung: Beweisen Sie mathematisch, ob die Entscheidungslogik des neuronalen Netzwerks durch eine kleine Menge symbolischer Logik vollständig abgedeckt (vollständig erklärt) werden kann. „Beweisen Sie, ob die Entscheidungslogik neuronaler Netze klar durch begrenzte symbolische Logik erklärt werden kann.“ Dieser Satz ist der grundlegende Satz zur Erklärung neuronaler Netze. Wenn dieser Vorschlag verfälscht wird, ist die Interpretierbarkeit neuronaler Netze grundsätzlich aussichtslos und alle interpretierenden Algorithmen können nur ungefähre Interpretationen liefern, aber nicht die gesamte Entscheidungslogik genau abdecken. Glücklicherweise haben wir drei gemeinsame Bedingungen für die okklusionsorientierte Robustheit gefunden, die neuronale Netze in den meisten Anwendungen erfüllen können, und mathematisch bewiesen, dass die Entscheidungslogik neuronaler Netze, die diese drei Bedingungen erfüllt, symbolisch als Interaktionskonzept geschrieben werden kann.
Siehe https://zhuanlan.zhihu.com/p/6937479462. Finden Sie nachweisbare und überprüfbare Grundursachen für Leistungsindikatoren: Kombinieren Sie die Generalisierung und Robustheit neuronaler Netze. Die Grundursache für ultimative Leistungsindikatoren B. die Leistung, wird in einige detaillierte Logiken unterteilt
. Die Interpretation der Leistung neuronaler Netze (Robustheit, Generalisierung) ist ein weiteres wichtiges Thema im Bereich der Interpretierbarkeit neuronaler Netze. Derzeit wird jedoch allgemein davon ausgegangen, dass die Leistung neuronaler Netze eine Beschreibung des neuronalen Netzes als Ganzes ist und dass neuronale Netze ihre Klassifizierungsurteile nicht wie Menschen in konkrete, kleine Mengen an Entscheidungslogik zerlegen können. In diesem Zusammenhang geben wir eine andere Perspektive und stellen eine mathematische Beziehung zwischen Leistungsindikatoren und konkreten Interaktionen her. Wir haben bewiesen, dass 1. die Komplexität äquivalenter Interaktionen direkt die gegnerische Robustheit/Übertragbarkeit neuronaler Netze bestimmen kann, 2. die Komplexität von Interaktionen die Darstellungsfähigkeit neuronaler Netze bestimmt und 3. die Generalisierungsfähigkeit neuronaler Netze erklärt [1], und 4. Erklären Sie den Darstellungsengpass neuronaler Netze.
Siehe 1: https://zhuanlan.zhihu.com/p/369883667
- Siehe 2: https://zhuanlan.zhihu.com/p/361686461
- Siehe 3: https://zhuanlan.zhihu.com/p/704760363
- Siehe 4: https://zhuanlan.zhihu.com/p/468569001
3. Unified Engineering Deep Learning Algorithmus
. Aufgrund des Mangels an grundlegender theoretischer Unterstützung sind die meisten aktuellen Deep-Learning-Algorithmen empirischer und technischer Natur. Die ersten Prinzipien im Bereich der Erklärbarkeit sollten in der Lage sein, die große Menge an Ingenieurerfahrungen früherer Generationen in wissenschaftliche Gesetze zusammenzufassen. Unter dem äquivalenten theoretischen System der Interaktionsinterpretierbarkeit hat unser Team bewiesen, dass die rechnerische Natur von 14 verschiedenen Algorithmen zur Zuordnung der Eingabewichtigkeit mathematisch in Form einer Umverteilung von Interaktionen vereinheitlicht werden kann. Darüber hinaus haben wir 12 Algorithmen zur Verbesserung der gegnerischen Übertragbarkeit vereinheitlicht und bewiesen, dass ein gemeinsamer Mechanismus aller Algorithmen zur Verbesserung der gegnerischen Übertragbarkeit darin besteht, den Interaktionseffekt zwischen gegnerischen Störungen zu reduzieren und so die meisten technischen Fähigkeiten in Richtung der theoretischen Interpretierbarkeit neuronaler Netze zu erreichen Verdichtung von Algorithmen.
- Siehe 1: https://zhuanlan.zhihu.com/p/610774894
- Siehe 2: https://zhuanlan.zhihu.com/p/546433296
Unter dem entsprechenden theoretischen System der interaktiven Interpretierbarkeit hat unser Team in früheren Forschungsarbeiten erfolgreich 20 CCF-A- und maschinelles Lern-Top-Konferenzbeiträge veröffentlicht. Wir haben die oben genannten Fragen theoretisch und experimentell vollständig beantwortet. 2. Überblick über die Forschung in diesem Artikel Es handelt sich um zwei Papiere. 1.Junpeng Zhang, Qing Li, Liang Lin, Quanshi Zhang, „Two-Phase Dynamics of Interactions Explains the Starting Point of a DNN Learning Over-Fitted Features“, in arXiv: 2405.10262 2. Qihan Ren, Yang Xu, Junpeng Zhang, Yue
Abbildung 1: Schematische Darstellung des zweistufigen Phänomens. In der ersten Stufe eliminiert das neuronale Netzwerk nach und nach Interaktionen mittlerer und hoher Ordnung und lernt Interaktionen niedriger Ordnung. Wenn die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust während des Trainingsprozesses des neuronalen Netzwerks zuzunehmen beginnt, tritt das neuronale Netzwerk zufällig in die zweite Trainingsphase ein. Wir hoffen, im entsprechenden Interaktionsrahmen eine neue Theorie vorschlagen zu können, um die Anzahl, Komplexität und Generalisierungsänderungen der vom neuronalen Netzwerk zu jedem Zeitpunkt gelernten Interaktionskonzepte genau vorherzusagen (dargestellt in Abbildung 1). Konkret hoffen wir, zwei Schlussfolgerungen beweisen zu können. Erstens wurde dies während des gesamten Trainingsprozesses auf der Grundlage des vorherigen Beweises (die Entscheidungslogik eines neuronalen Netzwerks kann streng dekonstruiert und als Summe des Nutzens von Dutzenden interaktiver Konzepte ausgedrückt werden) weiter rigoros abgeleitet , das neuronale Netzwerk Der dynamische Prozess der Änderung des modellierten Interaktionsnutzens –
Das heißt, die Theorie muss die Änderungen in der Verteilung der vom neuronalen Netzwerk modellierten Interaktionskonzepte in verschiedenen Trainingsstadien genau vorhersagen – um abzuleiten, welche Interaktionen auftreten werden verwendet zu welchem Zeitpunkt Gelernt . Zweitens suchen Sie nach ausreichenden Beweisen, um zu beweisen, dass die sich ändernden Regeln der abgeleiteten Interaktionskomplexität
objektiv die sich ändernden Regeln der Generalisierung des neuronalen Netzwerks während des Trainingszyklus widerspiegeln. Um die beiden oben genannten Punkte zusammenzufassen, hoffen wir, die eigentlichen Ursachen der Generalisierungsänderungen neuronaler Netze gründlich erklären zu können.
Beziehung zu Vorgängern: Natürlich kann jeder zuerst an den neuronalen Tangentenkern (NTK) denken [2], aber der neuronale Tangentenkern löst nur die Parameteränderungskurve und kann nicht weiter erklären Die Ebene der Entscheidungslogik stellt keine Beziehung zwischen der konzeptionellen Darstellung der neuronalen Netzwerkmodellierung und ihrer Generalisierung her. Die Analyse der Generalisierung bleibt immer noch auf der Ebene der Merkmalsraumanalyse, und es gibt keinen Zusammenhang zwischen [symbolisierter Konzeptlogik] und [. symbolisierte Konzeptlogik]. Es wird eine strikte Beziehung zwischen Generalisierbarkeit hergestellt. 3. Zwei wichtige Forschungshintergründe Missverständnis 1: Die primäre Darstellung des neuronalen Netzwerks ist die „äquivalente Interaktion“, nicht die Parameter und die Struktur des neuronalen Netzwerks. Die Analyse neuronaler Netze ausschließlich auf struktureller Ebene ist ein Missverständnis der grundlegenden Darstellung der Generalisierung neuronaler Netze. Derzeit konzentrieren sich die meisten Forschungen zur Generalisierung neuronaler Netze hauptsächlich auf die Struktur, Eigenschaften und Daten neuronaler Netze. Die Menschen glauben, dass unterschiedliche neuronale Netzwerkstrukturen von Natur aus unterschiedlichen Funktionen entsprechen und natürlich unterschiedliche Leistungen erbringen. Wie in Abbildung 2 dargestellt, handelt es sich bei dem Strukturunterschied jedoch nur um eine oberflächliche Form der Darstellung neuronaler Netze. Mit Ausnahme neuronaler Netze mit offensichtlichen Mängeln, die einen erheblichen Einfluss auf die Leistung haben, modellieren alle anderen neuronalen Netze mit unterschiedlichen Strukturen, die eine SOTA-Leistung erreichen können, häufig ähnliche äquivalente Interaktionsdarstellungen, dh leistungsstarke neuronale Netze mit unterschiedlichen Strukturen entsprechen interaktiven Darstellungen führen häufig durch unterschiedliche Ansätze zum gleichen Ziel [3, 4]. Obwohl die inneren Merkmale des neuronalen Netzwerks komplex und chaotisch sind, obwohl die von verschiedenen neuronalen Netzwerken modellierten Merkmalsvektoren sehr unterschiedlich sind und obwohl einzelne Neuronen im neuronalen Netzwerk häufig eine relativ verwirrende Semantik (nicht streng klare Semantik) modellieren, gilt dies für neuronale Netzwerke Netzwerk als Ganzes, beweisen wir theoretisch, dass die vom neuronalen Netzwerk modellierten Interaktionsbeziehungen spärlich und symbolisch sind (anstelle der spärlichen Anzahl von Merkmalen, siehe Kapitel „4. Definition der Interaktion“ für Einzelheiten) und auf dieselbe Aufgabe ausgerichtet sind . Unterschiedliche neuronale Netze modellieren oft ähnliche Interaktionen. Abbildung 2: Äquivalente Interaktionen, die durch neuronale Netze mit unterschiedlichen Strukturen modelliert werden, führen oft zum gleichen Ziel. Für einen identischen Eingabesatz modellieren zwei völlig unterschiedliche neuronale Netze, die auf dieselbe Aufgabe abzielen, häufig ähnliche Interaktionen. Aufgrund der unterschiedlichen Parameter und Trainingsmuster verschiedener neuronaler Netze weist kein Neuron in den beiden neuronalen Netzen eine strikte Eins-zu-eins-Entsprechung in der Darstellung auf, und jedes Neuron modelliert häufig unterschiedliche semantische Mischmuster. Im Gegensatz dazu sind die von neuronalen Netzen modellierten interaktiven Darstellungen, wie im vorherigen Absatz analysiert, tatsächlich Invarianten in verschiedenen Darstellungen neuronaler Netze. Daher haben wir Grund zu der Annahme, dass die grundlegende Darstellung neuronaler Netze eine äquivalente Interaktion ist und nicht deren Träger (Parameter und Trainingsbeispiele). Die symbolische Interaktionsdarstellung kann das erste Prinzip der Wissensdarstellung darstellen (interagiertes Sparsity-Theorem, Unendlichkeitssimulator). und das Phänomen, das gleiche Ziel auf verschiedenen Wegen zu erreichen, finden Sie im Kapitel „4. Definition von Interaktion“. Weitere Informationen finden Sie im folgenden Zhihu-Artikel /p/633531725 Missverständnis 2: Das Generalisierungsproblem neuronaler Netze ist ein gemischtes Modellproblem, kein Vektor in einem hochdimensionalen Raum Wie in Abbildung 3 gezeigt, geht die traditionelle Generalisierungsanalyse immer davon aus, dass es sich um ein einzelnes Modell handelt Probe ist ein Punkt in einem hochdimensionalen Raum. Tatsächlich erfolgt die Darstellung einer einzelnen Probe durch ein Mischungsmodell – tatsächlich ausgedrückt durch eine große Anzahl verschiedener Interaktionen Die Generalisierungsfähigkeit einfacher Interaktionen ist stärker als die komplexer Interaktionen. Daher ist es nicht mehr geeignet, die Generalisierungsfähigkeit des gesamten neuronalen Netzwerks auf verschiedenen Stichproben darzustellen Interaktionsbeziehungen unterschiedlicher Komplexität auf verschiedenen Proben entsprechen häufig unterschiedlichen Generalisierungsfähigkeiten. Durch neuronale Netze modellierte Interaktionen höherer Ordnung lassen sich häufig nur schwer auf Testproben übertragen (die gleichen Interaktionen werden nicht auf Testproben ausgelöst). , die Überanpassungsdarstellungen darstellen, und durch neuronale Netze modellierte Interaktionen niedriger Ordnung stellen häufig Darstellungen mit starker Verallgemeinerung dar. Weitere Informationen finden Sie in [1].Abbildung 3: (a) Die traditionelle Generalisierungsanalyse geht immer davon aus, dass eine einzelne Probe als Ganzes ein Punkt im hochdimensionalen Raum ist. (b) Tatsächlich stellt das neuronale Netzwerk eine einzelne Stichprobe in Form eines Mischungsmodells dar. Das neuronale Netzwerk modelliert einfache Interaktionen (verallgemeinerbare Interaktionen) und komplexe Interaktionen (nicht verallgemeinerbare Interaktionen) an einer einzelnen Stichprobe. 4. Definition von Interaktion . Es sei
eine skalare Ausgabe des DNN in der Stichprobe darstellen. Für ein auf Klassifizierungsaufgaben ausgerichtetes neuronales Netzwerk können wir seine skalare Ausgabe aus verschiedenen Perspektiven definieren. Beispielsweise kann für ein Klassifizierungsproblem mit mehreren Kategorien als oder als skalare Ausgabe definiert werden, die der wahren Bezeichnung der Probe vor der Softmax-Ebene entspricht. Hier stellt die Klassifizierungswahrscheinlichkeit der wahren Bezeichnung dar. Auf diese Weise können wir für jede Teilmenge die folgende Formel verwenden, um „Äquivalenz und Interaktion“ und „Äquivalenz oder Interaktion“ zwischen allen Eingabevariablen in  Wie in Abbildung 4(a) gezeigt, können wir die obige UND- oder Interaktion auf diese Weise verstehen: Wir können uns vorstellen, dass die UND-äquivalente Interaktion die „UND-Beziehung“ zwischen den Eingabevariablen in
Wie in Abbildung 4(a) gezeigt, können wir die obige UND- oder Interaktion auf diese Weise verstehen: Wir können uns vorstellen, dass die UND-äquivalente Interaktion die „UND-Beziehung“ zwischen den Eingabevariablen in  darstellt, die vom neuronalen Netzwerk codiert werden. Wenn beispielsweise ein Eingabesatz
darstellt, die vom neuronalen Netzwerk codiert werden. Wenn beispielsweise ein Eingabesatz  gegeben ist, könnte ein neuronales Netzwerk eine Interaktion zwischen
gegeben ist, könnte ein neuronales Netzwerk eine Interaktion zwischen  so modellieren, dass
so modellieren, dass  einen numerischen Nutzen erzeugt, der den „Regenguss“ der Ausgabe des neuronalen Netzwerks antreibt. Wenn eine Eingabevariable in
einen numerischen Nutzen erzeugt, der den „Regenguss“ der Ausgabe des neuronalen Netzwerks antreibt. Wenn eine Eingabevariable in  verdeckt ist, wird dieser numerische Nutzen aus der Ausgabe des neuronalen Netzwerks entfernt. In ähnlicher Weise stellt Äquivalenz oder Interaktion
verdeckt ist, wird dieser numerische Nutzen aus der Ausgabe des neuronalen Netzwerks entfernt. In ähnlicher Weise stellt Äquivalenz oder Interaktion  eine „ODER-Beziehung“ zwischen Eingabevariablen innerhalb von
eine „ODER-Beziehung“ zwischen Eingabevariablen innerhalb von  dar, die durch ein neuronales Netzwerk modelliert wird. Wenn beispielsweise ein Eingabesatz
dar, die durch ein neuronales Netzwerk modelliert wird. Wenn beispielsweise ein Eingabesatz  gegeben ist und ein Wort in
gegeben ist und ein Wort in  vorkommt, wird die Ausgabe des neuronalen Netzwerks zur Klassifizierung negativer Emotionen gesteuert. Die vom neuronalen Netzwerk modellierte äquivalente Interaktion erfüllt die drei axiomatischen Kriterien des „idealen Konzepts“, nämlich unendliche Anpassung, Sparsität und Übertragbarkeit zwischen Proben.
vorkommt, wird die Ausgabe des neuronalen Netzwerks zur Klassifizierung negativer Emotionen gesteuert. Die vom neuronalen Netzwerk modellierte äquivalente Interaktion erfüllt die drei axiomatischen Kriterien des „idealen Konzepts“, nämlich unendliche Anpassung, Sparsität und Übertragbarkeit zwischen Proben.
- Unendliche Anpassung: Wie in den Abbildungen 4 und 5 gezeigt, kann für jede Okklusionsprobe die Ausgabe des neuronalen Netzwerks auf der Probe durch die Summe der Nutzen verschiedener Interaktionskonzepte angepasst werden. Das heißt, wir können ein logisches Modell basierend auf der Interaktion erstellen. Unabhängig davon, wie wir die Eingabeprobe blockieren, kann dieses logische Modell den Ausgabewert des Modells in jedem blockierten Zustand der Eingabeprobe genau anpassen.
- Sparsity: Neuronale Netze für Klassifizierungsaufgaben modellieren oft nur eine kleine Anzahl signifikanter interaktiver Konzepte, und die meisten interaktiven Konzepte sind Rauschen mit einem numerischen Nutzen nahe 0.
- Übertragbarkeit zwischen Proben: Interaktionen sind zwischen verschiedenen Proben übertragbar, das heißt, signifikante Interaktionskonzepte, die von neuronalen Netzen an verschiedenen Proben (der gleichen Kategorie) modelliert werden, weisen häufig große Überlappungen auf.

Abbildung 4: Die komplexe Argumentationslogik neuronaler Netze kann durch ein Logikmodell basierend auf einer kleinen Anzahl von Interaktionen genau angepasst werden  . Jede Interaktion ist ein Maß für die nichtlineare Beziehung zwischen dem neuronalen Netzwerk und der Modellierung eines bestimmten Satzes von Eingabevariablen
. Jede Interaktion ist ein Maß für die nichtlineare Beziehung zwischen dem neuronalen Netzwerk und der Modellierung eines bestimmten Satzes von Eingabevariablen  . Wenn und nur wenn die Variablen im Satz gleichzeitig erscheinen, wird sie ausgelöst und interagiert und trägt einen numerischen Wert zur Ausgabe bei
. Wenn und nur wenn die Variablen im Satz gleichzeitig erscheinen, wird sie ausgelöst und interagiert und trägt einen numerischen Wert zur Ausgabe bei  Wenn eine Variable im Satz
Wenn eine Variable im Satz  erscheint, wird sie ausgelöst oder interagiert.
erscheint, wird sie ausgelöst oder interagiert. 
Abbildung 5: Die Ausgabe des neuronalen Netzwerks für jede Okklusionsstichprobe kann durch die Summe der Nutzen verschiedener Interaktionskonzepte angepasst werden, das heißt, wir können ein logisches Modell basierend auf der Interaktion konstruieren, unabhängig davon, wie wir die Eingabe verdecken Selbst wenn wir schlecht sind, kann dieses logische Modell beispielsweise bei einer völlig anderen Okklusionsmethode auf der Eingabeeinheit den Ausgabewert der Eingabeprobe des Modells in jedem Okklusionszustand genau anpassen. 5. Neue Entdeckungen und Beweise 5.1 Entdecken Sie das zweistufige Phänomen interaktiver Veränderungen in neuronalen Netzen während des Trainings 5 Konzentrieren Sie sich auf Ein grundlegendes Problem auf dem Gebiet der Interpretierbarkeit neuronaler Netze ist die Frage, wie die Änderungen der Generalisierungsfähigkeit des neuronalen Netzes während des Trainingsprozesses aus analytischer Analyseperspektive genau vorhergesagt und der Übergang des neuronalen Netzes von Unteranpassung zu Überanpassung genau analysiert werden können. Der gesamte dynamische Veränderungsprozess der Anprobe und die Ursachen dahinter . Zuerst definieren wir die Reihenfolge (Komplexität) einer Interaktion als die Anzahl der Eingabevariablen in der Interaktion, . Die frühere Arbeit unseres Teams ergab, dass die Komplexität der „Interaktion mit oder“, die von einem neuronalen Netzwerk in einer bestimmten Stichprobe modelliert wird, direkt die Generalisierungsfähigkeit des neuronalen Netzwerks in dieser Stichprobe bestimmt [1], d. h. die neuronale Ebene höherer Ordnung Netzwerkmodellierung. „UND-ODER-Interaktionen“ (zwischen einer großen Anzahl von Eingabeeinheiten) weisen tendenziell schlechte Generalisierungsfähigkeiten auf, während „UND-ODER-Interaktionen“ niedriger Ordnung (zwischen einer kleinen Anzahl von Eingabeeinheiten) starke Generalisierungsfähigkeiten aufweisen.
Daher besteht der erste Schritt dieser Forschung darin, eine analytische Lösung für die Komplexität verschiedener Ordnungen von „UND-ODER-Interaktionen“ vorherzusagen, die vom neuronalen Netzwerk zu verschiedenen Zeitpunkten während des Trainingsprozesses modelliert werden, d. h. Wir können die Generalisierungsfähigkeit des neuronalen Netzwerks in verschiedenen Phasen durch die Verteilung verschiedener Ordnungen von „UND oder Interaktion“ erklären, die das neuronale Netzwerk zu verschiedenen Zeitpunkten modelliert. Zur Definition der Generalisierungsfähigkeit der Interaktion und zur Definition der gesamten Generalisierungsfähigkeit des neuronalen Netzwerks lesen Sie bitte das Kapitel „5.2 Die Beziehung zwischen der durch das neuronale Netzwerk modellierten Interaktionsreihenfolge und seiner Generalisierungsfähigkeit“. Wir schlagen zwei Indikatoren vor, um die Verteilung der Intensität von Interaktionen unterschiedlicher Ordnung (Komplexität) darzustellen. Insbesondere verwenden wir
, um die Stärke aller positiven signifikanten Wechselwirkungen der Ordnung zu messen, und , um die Stärke aller negativen signifikanten Wechselwirkungen der Ordnung zu messen, wobei und die Menge der signifikanten Interaktionen darstellen und den Schwellenwert der Signifikanz darstellt Interaktion. Abbildung 6: Unterschiedliche Ordnungsinteraktionsstärken  und
und  extrahiert aus neuronalen Netzen, die für verschiedene Runden trainiert wurden. Der Trainingsprozess verschiedener neuronaler Netze, die auf unterschiedlichen Datensätzen und unterschiedlichen Aufgaben trainiert werden, weist ein zweistufiges Phänomen auf. Die ersten beiden ausgewählten Zeitpunkte gehören zur ersten Phase, während die letzten beiden Zeitpunkte zur zweiten Phase gehören. Gerade kurz nach Eintritt in die zweite Phase des neuronalen Netztrainingsprozesses beginnt die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust des neuronalen Netzes deutlich anzusteigen (siehe letzte Spalte). Dies zeigt, dass das zweistufige Phänomen des neuronalen Netzwerktrainings zeitlich an Änderungen der Modellverlustlücke „ausgerichtet“ wird. Weitere experimentelle Ergebnisse finden Sie im Artikel. Wie in Abbildung 6 gezeigt, manifestiert sich das zweistufige Phänomen des neuronalen Netzwerks insbesondere wie folgt:
extrahiert aus neuronalen Netzen, die für verschiedene Runden trainiert wurden. Der Trainingsprozess verschiedener neuronaler Netze, die auf unterschiedlichen Datensätzen und unterschiedlichen Aufgaben trainiert werden, weist ein zweistufiges Phänomen auf. Die ersten beiden ausgewählten Zeitpunkte gehören zur ersten Phase, während die letzten beiden Zeitpunkte zur zweiten Phase gehören. Gerade kurz nach Eintritt in die zweite Phase des neuronalen Netztrainingsprozesses beginnt die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust des neuronalen Netzes deutlich anzusteigen (siehe letzte Spalte). Dies zeigt, dass das zweistufige Phänomen des neuronalen Netzwerktrainings zeitlich an Änderungen der Modellverlustlücke „ausgerichtet“ wird. Weitere experimentelle Ergebnisse finden Sie im Artikel. Wie in Abbildung 6 gezeigt, manifestiert sich das zweistufige Phänomen des neuronalen Netzwerks insbesondere wie folgt:
- Vor dem neuronalen Training codiert das initialisierte neuronale Netzwerk hauptsächlich mittel- Interaktionen höherer und niedrigerer Ordnung werden selten kodiert und die Verteilung von Interaktionen unterschiedlicher Ordnung scheint „spindelförmig“ zu sein. Unter der Annahme, dass das neuronale Netzwerk mit zufälligen Initialisierungsparametern reines Rauschen modelliert, haben wir in „5.4 Theoretischer Beweis des zweistufigen Phänomens“ bewiesen, dass die vom neuronalen Netzwerk mit zufälligen Initialisierungsparametern modellierte Verteilung von Interaktionen unterschiedlicher Ordnung eine „Spindelform“ aufweist „Das heißt, es wird nur eine kleine Anzahl von Interaktionen niedriger und hoher Ordnung modelliert, während eine große Anzahl von Interaktionen mittlerer Ordnung modelliert wird.
- In der ersten Phase des neuronalen Netzwerktrainings schwächt sich die Stärke der vom neuronalen Netzwerk codierten Interaktionen hoher und mittlerer Ordnung allmählich ab, während die Stärke der Interaktionen niedriger Ordnung allmählich zunimmt. Schließlich werden Interaktionen hoher und mittlerer Ordnung nach und nach eliminiert, und das neuronale Netzwerk kodiert nur noch Interaktionen niedriger Ordnung.
- In der zweiten Phase des neuronalen Netzwerktrainings nimmt die vom neuronalen Netzwerk codierte Interaktionsreihenfolge (Komplexität) während des Trainingsprozesses allmählich zu. Mit dem schrittweisen Erlernen komplexerer Interaktionen steigt auch allmählich das Risiko einer Überanpassung neuronaler Netze.
Das obige zweistufige Phänomen kommt häufig im Trainingsprozess neuronaler Netze mit unterschiedlichen Strukturen auf unterschiedlichen Datensätzen und unterschiedlichen Aufgaben vor. Wir haben VGG-13.11.16 auf Bilddatensätzen (CIFAR-10-Datensatz, MNIST-Datensatz, CUB200-2011-Datensatz (unter Verwendung von aus Bildern ausgeschnittenen Vogelbildern) und Tiny-ImageNet-Datensatz) und AlexNet trainiert. Wir haben das Bert-Medium/Tiny-Modell für die semantische Stimmungsklassifizierung auf dem SST-2-Datensatz trainiert, und wir haben DGCNN auf dem ShapeNet-Datensatz trainiert, um 3D-Punktwolkendaten zu klassifizieren. Die obige Abbildung zeigt die Verteilung signifikanter Interaktionen unterschiedlicher Ordnung, die von verschiedenen neuronalen Netzen in verschiedenen Trainingsepochen extrahiert wurden. Wir haben während des Trainingsprozesses dieser neuronalen Netze zweistufige Phänomene entdeckt. Weitere experimentelle Ergebnisse und Details finden Sie im Artikel. 5.2 Die Beziehung zwischen der durch ein neuronales Netzwerk modellierten Interaktionsreihenfolge und seiner Generalisierungsfähigkeit , Interaktionen höherer Ordnung haben eine schlechtere Generalisierungsfähigkeit als Interaktionen niedriger Ordnung [1]. Die Generalisierbarkeit einer bestimmten Interaktion ist klar definiert – wenn eine Interaktion sowohl in Trainingsproben als auch in Testproben häufig vom neuronalen Netzwerk modelliert wird, weist diese Interaktion eine gute Generalisierungsfähigkeit auf. In diesem Zhihu-Artikel werden zwei Experimente vorgestellt, um zu beweisen, dass Wechselwirkungen hoher Ordnung über schlechte Generalisierungsfähigkeiten und Wechselwirkungen niedriger Ordnung über starke Generalisierungsfähigkeiten verfügen. Experiment 1: Beobachten Sie die Verallgemeinerung von Interaktionen, die von verschiedenen neuronalen Netzen modelliert werden, die auf verschiedenen Datensätzen trainiert wurden. Hier verwenden wir die Jaccard-Ähnlichkeit zwischen der Verteilung der durch den Testsatz ausgelösten Interaktionen und der Verteilung der durch den Trainingssatz ausgelösten Interaktionen, um die Verallgemeinerung der Interaktion zu messen.Konkret vektorisieren wir anhand einer Eingabeprobe  , die
, die  Eingabevariablen enthält,
Eingabevariablen enthält,  die aus der Eingabeprobe
die aus der Eingabeprobe  extrahierten
extrahierten  -Ordnungsinteraktionen, wobei
-Ordnungsinteraktionen, wobei 

 -Ordnungsinteraktionen darstellt. Anschließend berechnen wir den durchschnittlichen Interaktionsvektor der Ordnung
-Ordnungsinteraktionen darstellt. Anschließend berechnen wir den durchschnittlichen Interaktionsvektor der Ordnung  , der aus allen Stichproben mit der Kategorie
, der aus allen Stichproben mit der Kategorie  in der Klassifizierungsaufgabe extrahiert wurde, ausgedrückt als
in der Klassifizierungsaufgabe extrahiert wurde, ausgedrückt als  , wobei
, wobei  die Menge der Stichproben mit der Kategorie
die Menge der Stichproben mit der Kategorie  darstellt.Als nächstes berechnen wir die Jaccard-Ähnlichkeit zwischen dem durchschnittlichen Interaktionsvektor
darstellt.Als nächstes berechnen wir die Jaccard-Ähnlichkeit zwischen dem durchschnittlichen Interaktionsvektor  der Ordnung
der Ordnung  , der aus den Trainingsproben extrahiert wurde, und dem durchschnittlichen Interaktionsvektor
, der aus den Trainingsproben extrahiert wurde, und dem durchschnittlichen Interaktionsvektor  der Ordnung
der Ordnung  , der aus den Testproben extrahiert wurde, um die
, der aus den Testproben extrahiert wurde, um die  der Proben mit der Kategorie in der Klassifizierungsaufgabe zu messen Generalisierungsfähigkeit der Ordnungsinteraktion, das heißt:
der Proben mit der Kategorie in der Klassifizierungsaufgabe zu messen Generalisierungsfähigkeit der Ordnungsinteraktion, das heißt: 
 wobei
wobei  und
und  zwei
zwei  -dimensionale Interaktionsvektoren auf zwei -dimensionale nichtnegative Vektoren projizieren, um die Jaccard-Ähnlichkeit zu berechnen. Wenn für eine Interaktion einer bestimmten Reihenfolge diese Interaktionsreihenfolge im Allgemeinen eine große Jaccard-Ähnlichkeit aufweist, bedeutet dies, dass diese Interaktionsreihenfolge eine starke Generalisierungsfähigkeit aufweist.
-dimensionale Interaktionsvektoren auf zwei -dimensionale nichtnegative Vektoren projizieren, um die Jaccard-Ähnlichkeit zu berechnen. Wenn für eine Interaktion einer bestimmten Reihenfolge diese Interaktionsreihenfolge im Allgemeinen eine große Jaccard-Ähnlichkeit aufweist, bedeutet dies, dass diese Interaktionsreihenfolge eine starke Generalisierungsfähigkeit aufweist.  Wir haben Experimente durchgeführt, um verschiedene Bestellinteraktionen zu berechnen
Wir haben Experimente durchgeführt, um verschiedene Bestellinteraktionen zu berechnen . Wir haben LeNet getestet, das auf dem MNIST-Datensatz trainiert wurde, VGG-11, das auf dem CIFAR-10-Datensatz trainiert wurde, VGG-13, das auf dem CUB200-2011-Datensatz trainiert wurde, und AlexNet, das auf dem Tiny-ImageNet-Datensatz trainiert wurde. Um den Rechenaufwand zu reduzieren, haben wir nur die durchschnittliche Jaccard-Ähnlichkeit der Top-10-Kategorien berechnet. Wie in Abbildung 7 dargestellt, nimmt die Jaccard-Ähnlichkeit der Interaktion mit zunehmender Interaktionsreihenfolge weiter ab. Dies bestätigt daher, dass Interaktionen höherer Ordnung schlechtere Generalisierungsfähigkeiten aufweisen als Interaktionen niedrigerer Ordnung. Abbildung 7: Jaccard-Ähnlichkeit zwischen Interaktionen, die aus Trainings- und Testproben extrahiert wurden. Die relativ hohe Jaccard-Ähnlichkeit von Wechselwirkungen niedriger Ordnung weist darauf hin, dass Wechselwirkungen niedriger Ordnung eine starke Generalisierungsfähigkeit aufweisen.
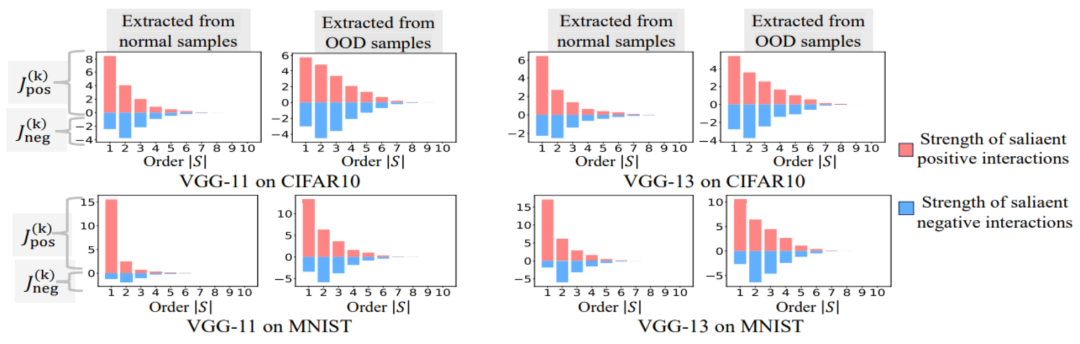
. Wir haben LeNet getestet, das auf dem MNIST-Datensatz trainiert wurde, VGG-11, das auf dem CIFAR-10-Datensatz trainiert wurde, VGG-13, das auf dem CUB200-2011-Datensatz trainiert wurde, und AlexNet, das auf dem Tiny-ImageNet-Datensatz trainiert wurde. Um den Rechenaufwand zu reduzieren, haben wir nur die durchschnittliche Jaccard-Ähnlichkeit der Top-10-Kategorien berechnet. Wie in Abbildung 7 dargestellt, nimmt die Jaccard-Ähnlichkeit der Interaktion mit zunehmender Interaktionsreihenfolge weiter ab. Dies bestätigt daher, dass Interaktionen höherer Ordnung schlechtere Generalisierungsfähigkeiten aufweisen als Interaktionen niedrigerer Ordnung. Abbildung 7: Jaccard-Ähnlichkeit zwischen Interaktionen, die aus Trainings- und Testproben extrahiert wurden. Die relativ hohe Jaccard-Ähnlichkeit von Wechselwirkungen niedriger Ordnung weist darauf hin, dass Wechselwirkungen niedriger Ordnung eine starke Generalisierungsfähigkeit aufweisen.  실험 2: 일반 샘플과 OOD 샘플에서 신경망으로 모델링한 상호작용 분포 비교. 우리는 신경망이 OOD 샘플에서 더 고차 상호 작용을 모델링하는지 여부를 조사하기 위해 일반 샘플에서 추출된 상호 작용과 OOD(Out-of-Distribution) 샘플에서 추출된 상호 작용을 비교했습니다. 소수의 훈련 샘플의 분류 라벨을 잘못된 라벨로 설정했습니다. 이런 방식으로 데이터 세트의 원래 샘플은 일반 샘플로 간주될 수 있지만 잘못된 레이블이 있는 일부 샘플은 OOD 샘플에 해당하며 이러한 OOD 샘플은 신경망의 과적합을 유발할 수 있습니다. 우리는 MNIST 데이터세트와 CIFAR-10 데이터세트에서 각각 VGG-11과 VGG-13을 훈련했습니다. 그림 8은 일반 샘플에서 추출된 상호 작용의 분포와 OOD 샘플에서 추출된 상호 작용의 분포를 비교합니다. 우리는 VGG-11과 VGG-13이 OOD 샘플을 분류할 때 더 복잡한 상호작용(고차 상호작용)을 모델링하는 반면, 일반 샘플을 분류할 때는 저차 상호작용이 사용된다는 것을 발견했습니다. 이는 고차 상호작용의 일반화 능력이 일반적으로 저차 상호작용의 일반화 능력보다 약하다는 것을 검증합니다.
실험 2: 일반 샘플과 OOD 샘플에서 신경망으로 모델링한 상호작용 분포 비교. 우리는 신경망이 OOD 샘플에서 더 고차 상호 작용을 모델링하는지 여부를 조사하기 위해 일반 샘플에서 추출된 상호 작용과 OOD(Out-of-Distribution) 샘플에서 추출된 상호 작용을 비교했습니다. 소수의 훈련 샘플의 분류 라벨을 잘못된 라벨로 설정했습니다. 이런 방식으로 데이터 세트의 원래 샘플은 일반 샘플로 간주될 수 있지만 잘못된 레이블이 있는 일부 샘플은 OOD 샘플에 해당하며 이러한 OOD 샘플은 신경망의 과적합을 유발할 수 있습니다. 우리는 MNIST 데이터세트와 CIFAR-10 데이터세트에서 각각 VGG-11과 VGG-13을 훈련했습니다. 그림 8은 일반 샘플에서 추출된 상호 작용의 분포와 OOD 샘플에서 추출된 상호 작용의 분포를 비교합니다. 우리는 VGG-11과 VGG-13이 OOD 샘플을 분류할 때 더 복잡한 상호작용(고차 상호작용)을 모델링하는 반면, 일반 샘플을 분류할 때는 저차 상호작용이 사용된다는 것을 발견했습니다. 이는 고차 상호작용의 일반화 능력이 일반적으로 저차 상호작용의 일반화 능력보다 약하다는 것을 검증합니다. 
그림 8: 일반 표본에서 추출한 상호 작용과 분포(OOD) 표본에서 추출한 상호 작용을 비교합니다. 신경망은 일반적으로 OOD 샘플에 대한 고차 상호 작용을 모델링합니다.
5.3 신경망 훈련 과정 중 2단계 현상과 손실 격차의 변화는 비교적 일관적입니다.
위의 2단계 현상이 일반화를 완벽하게 나타낼 수 있음을 발견했습니다. 신경망의 역학. 매우 흥미로운 현상은 신경망 훈련 과정의 2단계 현상과 테스트 세트와 훈련 세트의 신경망 손실 격차의 변화가 시간적으로 정렬된다는 것입니다. 훈련 손실과 테스트 손실 간의 손실 격차는 모델 과적합 정도를 측정하는 데 가장 널리 사용되는 측정항목입니다. 그림 6은 다양한 신경망에 대한 학습 프로젝트의 테스트 손실과 학습 손실 간의 손실 격차 곡선을 보여주며, 다양한 학습 에포크에서 신경망에서 추출된 상호 작용 분포도 보여줍니다. 우리는 신경망 훈련 과정에서 테스트 손실과 훈련 손실 사이의 손실 격차가 증가하기 시작하면 신경망이 우연히 훈련의 두 번째 단계에 진입한다는 것을 발견했습니다. 이는 신경망 훈련의 2단계 현상이 모델 손실 격차의 변화에 맞춰 "정렬"된다는 것을 보여줍니다. 위의 현상을 이렇게 이해할 수 있습니다. 훈련 과정이 시작되기 전에 초기화된 신경망에 의해 모델링된 상호 작용은 모두 무작위 노이즈를 나타내며 서로 다른 순서의 상호 작용 분포는 "스핀들"처럼 보입니다. 신경망 훈련의 첫 번째 단계에서 신경망은 점차적으로 중간 및 고차 상호 작용을 제거하고 가장 간단한(최하위) 상호 작용을 학습합니다. 그런 다음 신경망 훈련의 두 번째 단계에서 신경망은 증가하는 순서의 상호 작용을 모델링합니다. "5.2 신경망으로 모델링된 상호 작용의 순서와 일반화 능력의 관계" 장에서 두 번의 실험을 통해 고차 상호 작용이 일반적으로 저차 상호 작용보다 일반화 능력이 떨어진다는 것을 확인했기 때문에 두 번째 단계에서 생각할 수 있습니다. 신경망 훈련의 경우 DNN은 먼저 가장 강력한 일반화 능력을 갖춘 상호 작용을 학습한 다음 점차 일반화 능력이 약한 더 복잡한 상호 작용으로 이동합니다. 결국 일부 신경망은 점차적으로 과적합되어 다수의 중간 및 고차원 상호 작용을 인코딩합니다.
신경망 훈련 과정의 2단계 현상이 세 부분으로 나누어진다는 것을 이론적으로 증명해야 합니다. 훈련 과정이 시작되기 전에 무작위로 초기화된 신경망 모델링된 상호작용의 분포는 "스핀들 모양"을 나타냅니다. 즉, 고차 및 저차 상호작용은 거의 모델링되지 않고 중간차 상호작용이 주로 모델링됩니다. 두 번째 부분에서는 신경망이 훈련의 두 번째 단계에서 점점 더 큰 상호 작용을 모델링한다는 것을 보여줍니다. 섹션 3에서는 신경망이 훈련의 첫 번째 단계에서 중간 및 고차원 상호 작용을 점차적으로 제거하고 최저 비용 상호 작용을 학습한다는 것을 보여줍니다.
1. 초기화 신경망 모델링을 위한 "스핀들" 상호 작용 분포를 증명합니다. 무작위로 초기화된 무작위 네트워크 모델은 훈련 과정이 시작되기 전에 노이즈가 발생하므로 무작위로 초기화된 신경망에 의해 모델링된 상호 작용은 평균
및 분산 을 갖는 정규 분포를 따른다고 가정합니다. 위의 가정 하에서, 우리는 초기화된 신경망에 의해 모델링된 상호 작용의 강도 합 분포가 "스핀들 모양"을 나타냄을 보여줄 수 있었습니다. 주문 상호 작용. 2. 신경망 훈련의 두 번째 단계에서 대화형 변화의 동적 프로세스를 증명합니다. 정식 인증에 들어가기 전에 다음과 같은 준비 작업을 해야 합니다. 먼저, 우리는 [5, 6]의 접근 방식을 따르고 다양한 상호 작용 트리거 함수의 가중 합계  로 특정 샘플에 대한 신경망 추론 을 다시 작성합니다.
로 특정 샘플에 대한 신경망 추론 을 다시 작성합니다.  여기서
여기서  는 만족스러운 스칼라 가중치입니다
는 만족스러운 스칼라 가중치입니다  .
.  기능은 모든 교합 샘플
기능은 모든 교합 샘플  에서
에서  을 만족시키는 대화형 트리거 기능입니다. 함수
을 만족시키는 대화형 트리거 기능입니다. 함수  의 특정 형태는 Taylor 확장에서 파생될 수 있습니다. 논문을 참조하세요. 여기서는 설명하지 않습니다.
의 특정 형태는 Taylor 확장에서 파생될 수 있습니다. 논문을 참조하세요. 여기서는 설명하지 않습니다.
위에서 다시 작성한 형식에 따르면 특정 샘플에 대한 신경망 학습은 대략적으로 대화형 트리거 기능의 가중치 에 대한 학습으로 간주할 수 있습니다. 또한, 실험실의 예비 작업[3]에서는 동일한 작업에 대해 완전히 훈련된 서로 다른 신경망이 유사한 상호 작용을 모델링하는 경향이 있음을 발견했습니다. 따라서 신경망 학습을 일련의 잠재적인 실제 상호 작용으로 간주할 수 있습니다. 따라서 신경망이 수렴하도록 훈련될 때 모델링된 상호 작용은 다음 목적 함수를 최소화할 때 얻은 솔루션으로 볼 수 있습니다.
에 대한 학습으로 간주할 수 있습니다. 또한, 실험실의 예비 작업[3]에서는 동일한 작업에 대해 완전히 훈련된 서로 다른 신경망이 유사한 상호 작용을 모델링하는 경향이 있음을 발견했습니다. 따라서 신경망 학습을 일련의 잠재적인 실제 상호 작용으로 간주할 수 있습니다. 따라서 신경망이 수렴하도록 훈련될 때 모델링된 상호 작용은 다음 목적 함수를 최소화할 때 얻은 솔루션으로 볼 수 있습니다.  여기서
여기서  는 신경망이 적합해야 하는 일련의 잠재적인 Ground Truth 상호 작용을 나타냅니다.
는 신경망이 적합해야 하는 일련의 잠재적인 Ground Truth 상호 작용을 나타냅니다.  과
과  는 각각 모든 가중치를 합친 벡터와 모든 상호작용 트리거 함수의 값을 합친 벡터를 나타냅니다.
는 각각 모든 가중치를 합친 벡터와 모든 상호작용 트리거 함수의 값을 합친 벡터를 나타냅니다.
불행하게도 위의 모델링은 신경망이 융합으로 훈련될 때 상호작용을 얻을 수 있지만, 신경망 훈련 과정에서 상호작용을 학습하는 동적 과정을 잘 설명할 수는 없습니다. 여기서는 핵심 가설을 소개합니다. 초기화된 신경망의 매개 변수에는 많은 양의 잡음이 포함되어 있으며 이러한 잡음의 크기는 훈련 과정에서 점차 작아진다고 가정합니다. 또한 매개변수의 노이즈는 상호작용 트리거 기능의 노이즈로 이어지며() 이 노이즈는 상호작용 순서에 따라 기하급수적으로 증가합니다([5]에서 실험적으로 관찰되고 검증되었습니다). 우리는 다음과 같이 잡음이 있는 신경망 학습을 모델링합니다. 
소음이  만족되는 곳
만족되는 곳  . 그리고 훈련이 진행됨에 따라 노이즈의 분산
. 그리고 훈련이 진행됨에 따라 노이즈의 분산 은 점차 작아집니다. 주어진 노이즈 레벨
은 점차 작아집니다. 주어진 노이즈 레벨 에 대해 위의 손실 함수를 최소화하면 아래 그림의 정리와 같이 최적 상호 작용 가중치
에 대해 위의 손실 함수를 최소화하면 아래 그림의 정리와 같이 최적 상호 작용 가중치  의 분석 솔루션 을 얻을 수 있습니다.
의 분석 솔루션 을 얻을 수 있습니다.

우리는 훈련이 진행됨에 따라(즉, 잡음 크기  가 작아짐), 저차 및 중차 상호 작용 강도 대 고차 상호 작용 강도의 비율이 점차 감소한다는 것을 발견했습니다 (그림에 표시된 대로) 아래 정리). 이는 신경망이 훈련의 두 번째 단계에서 점차적으로 고차 상호작용을 학습하는 현상을 설명합니다.
가 작아짐), 저차 및 중차 상호 작용 강도 대 고차 상호 작용 강도의 비율이 점차 감소한다는 것을 발견했습니다 (그림에 표시된 대로) 아래 정리). 이는 신경망이 훈련의 두 번째 단계에서 점차적으로 고차 상호작용을 학습하는 현상을 설명합니다. 
또한 위의 결론을 추가로 실험적으로 검증했습니다. n개의 입력 단위가 있는 샘플이 주어지면 미터법  (여기서
(여기서  )을 사용하여 k+1차 상호 작용에 대한 k차 상호 작용의 강도 비율을 대략적으로 측정할 수 있습니다. 아래 그림에서 서로 다른 입력 단위 수 n과 서로 다른 차수 k에서
)을 사용하여 k+1차 상호 작용에 대한 k차 상호 작용의 강도 비율을 대략적으로 측정할 수 있습니다. 아래 그림에서 서로 다른 입력 단위 수 n과 서로 다른 차수 k에서  이 감소함에 따라 비율이 점차 감소하는 것을 확인할 수 있습니다.
이 감소함에 따라 비율이 점차 감소하는 것을 확인할 수 있습니다. 
그림 9: 서로 다른 입력 장치 수 n과 서로 다른 차수 k에서 k차 상호 작용 비율과 k+1차 상호 작용 강도는 소음 수준에 따라 변경됩니다.  점차 감소합니다. . 이는 훈련이 진행됨에 따라(즉,
점차 감소합니다. . 이는 훈련이 진행됨에 따라(즉,  점차 작아짐), 저차 상호작용 강도와 고차 상호작용 강도의 비율이 점차 작아지고, 신경망이 점차 고차 상호작용을 학습한다는 것을 보여줍니다. ㅋㅋㅋ 이론 상호작용 분포는 실제 훈련의 각 시점에서의 상호작용 강도 분포를 잘 예측할 수 있습니다. 그림 10: 이론적 상호 작용 분포
점차 작아짐), 저차 상호작용 강도와 고차 상호작용 강도의 비율이 점차 작아지고, 신경망이 점차 고차 상호작용을 학습한다는 것을 보여줍니다. ㅋㅋㅋ 이론 상호작용 분포는 실제 훈련의 각 시점에서의 상호작용 강도 분포를 잘 예측할 수 있습니다. 그림 10: 이론적 상호 작용 분포  (파란색 히스토그램)과 실제 상호 작용 분포
(파란색 히스토그램)과 실제 상호 작용 분포  (주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 3. 신경망 훈련의 첫 번째 단계에서 대화형 변화의 동적 프로세스를 증명합니다. 훈련의 두 번째 단계에서 상호 작용의 동적 변화를 소음
(주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 3. 신경망 훈련의 첫 번째 단계에서 대화형 변화의 동적 프로세스를 증명합니다. 훈련의 두 번째 단계에서 상호 작용의 동적 변화를 소음 
 이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 갈 길이 멀다. 우리 팀은 이 이론을 더 많은 측면에서 확고히 하고 등가 상호 작용이 상징적 설명이라는 것을 엄격하게 증명할 수 있기를 바랍니다. , 신경망 표현의 병목 현상을 입증하고 신경망의 마이그레이션 저항성을 향상시키는 12가지 방법을 통합하고 14가지 중요도 추정 방법을 설명하는 동시에 신경망의 일반화 및 견고성을 설명할 수 있습니다. 나중에 이론적인 시스템을 더욱 개선하기 위해 더욱 탄탄한 작업을 하도록 하겠습니다. [1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang이 대화형 개념을 사용하여 DNS의 일반화 능력을 설명합니다., 2024 [2] Arthur Jacot, Franck Gabriel, 신경 탄젠트 커널: 신경망의 수렴 및 일반화. NeurIPS, 2018[3] 신경망은 실제로 ICML을 인코딩합니까? , 2023[4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li 및 Quanshi Zhang. 대규모 언어 모델의 추론 논리를 상징적 개념으로 풀 수 있습니까?[5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou 및 Quanshi Zhang. ICML, 2023[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi. Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움. NeurIPS, 2023
이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 갈 길이 멀다. 우리 팀은 이 이론을 더 많은 측면에서 확고히 하고 등가 상호 작용이 상징적 설명이라는 것을 엄격하게 증명할 수 있기를 바랍니다. , 신경망 표현의 병목 현상을 입증하고 신경망의 마이그레이션 저항성을 향상시키는 12가지 방법을 통합하고 14가지 중요도 추정 방법을 설명하는 동시에 신경망의 일반화 및 견고성을 설명할 수 있습니다. 나중에 이론적인 시스템을 더욱 개선하기 위해 더욱 탄탄한 작업을 하도록 하겠습니다. [1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang이 대화형 개념을 사용하여 DNS의 일반화 능력을 설명합니다., 2024 [2] Arthur Jacot, Franck Gabriel, 신경 탄젠트 커널: 신경망의 수렴 및 일반화. NeurIPS, 2018[3] 신경망은 실제로 ICML을 인코딩합니까? , 2023[4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li 및 Quanshi Zhang. 대규모 언어 모델의 추론 논리를 상징적 개념으로 풀 수 있습니까?[5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou 및 Quanshi Zhang. ICML, 2023[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi. Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움. NeurIPS, 2023등가 상호 작용 이론 시스템
[1] Huiqi Deng, Na Zou, Mengnan Du, Weifu Chen, Guocan Feng, Ziwei Yang, Zheyang Li, Quanshi Zhang. Taylor 상호 작용을 통해 14가지 사후 기여 분석 방법 통합. 패턴 분석 및 기계 지능(IEEE T-PAMI)에 대한 IEEE 트랜잭션, 2024.
[2] Xu Cheng, Lei Cheng , Zhaoran Peng, Yang Xu, Tian Han 및 Quanshi Zhang. ICML, 2024.
[3] Qihan Ren, Jiayang Gao, Wen Shen 및 Quanshi Zhang. AI 모델에서 희소 상호 작용 프리미티브의 출현 증명, 2024.
[4] Lu Chen, Siyu Lou, Benhao Huang 및 Quanshi Zhang ICLR에서 일반화 가능한 상호 작용 프리미티브 정의 및 추출, 2024.
[5] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang. 대화형 개념을 사용하여 DNN의 일반화 기능 설명, 2024.
[ 6 ] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움, 2023.
[7] Quanshi Zhang, Jie Ren, Ge Huang, Ruiming Cao, Ying Nian Wu 및 Song-Chun Zhu. 패턴 분석 및 기계 지능에 대한 IEEE 트랜잭션을 통한 컨볼루셔널 네트워크의 해석 가능한 AOG 표현 마이닝. -PAMI), 2020.
[8] Xin Wang, Jie Ren, Shuyun Lin, Xiangming Zhu, Yisen Wang, Quanshi Zhang. ICLR 해석 및 향상을 위한 통합 접근 방식, 2021.
[9] Hao Zhang, Sen Li, Yinchao Ma, Mingjie Li, Yichen Xie 및 Quanshi Zhang. ICLR에서 탈락 해석 및 향상, 2021.
[10] Mingjie Li 및 Quanshi Zhang. . 신경망은 실제로 상징적 개념을 인코딩합니까?, 2023.
[11] Lu Chen, Siyu Lou, Keyan Zhang, Jin Huang 및 Quanshi Zhang: 단일 순방향 전파에서 정확한 Shapley 값 계산. . ICML , 2023.
[12] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou 및 Quanshi Zhang. 섭동에 민감하고 복잡한 개념을 인코딩하지 않음, 2023.
[13 ] Jie Ren, Mingjie Li, Qirui Chen, Huiqi Deng 및 Quanshi Zhang. CVPR에서 희소 개념의 출현 정의 및 정량화, 2023.
[14] Jie Ren, Mingjie Li, Meng Zhou, Shih- Han Chan 및 Quanshi Zhang. ReLU DNN의 변환 복잡성에 대한 이론적 분석, 2022.
[15] Jie Ren, Die Zhang, Yisen Wang, Lu Chen, Zhanpeng Zhou, Yiting Chen, Xu Cheng, Xin Wang, Meng Zhou, Jie Shi 및 Quanshi Zhang. NeurIPS, 2021.
[16] Wen Shen, Qihan Ren, Dongrui Liu 및 Quanshi Zhang. 3D 포인트 클라우드 처리를 위한 DNN, 2021.
[17] Xin Wang, Shuyun Lin, Hao Zhang, Yufei Zhu 및 Quanshi Zhang. ICCV의 속성 및 상호 작용 해석, 2021. Zhihua Wei, Shikun Huang, Binbin Zhang, Panyue Chen, Ping Zhao 및 Quanshi Zhang. 검증 가능성 및 예측 가능성: CVPR을 위한 네트워크 아키텍처의 유틸리티 해석, 2021.
[19] Hao Zhang, Yichen Xie. , Longjie Zheng, Die Zhang 및 Quanshi Zhang. AAAI에서 다변량 Shapley 상호 작용 해석, 2021.
[20] Die Zhang, Huilin Zhou, Hao Zhang, Xiaoyi Bao, Da Huo, Ruizhao Chen, Xu Cheng, Mengyue Wu 및 Quanshi Zhang. 심층 NLP 모델을 위한 해석 가능한 상호 작용 트리 구축, 2021.
Das obige ist der detaillierte Inhalt vonDie ultimative Frage der Erklärbarkeit lautet: Was ist die erste Erklärung? 20 CCF-A+ICLR-Artikel geben Ihnen Antworten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

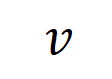
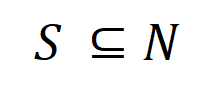 darstellt, die vom neuronalen Netzwerk codiert werden. Wenn beispielsweise ein Eingabesatz
darstellt, die vom neuronalen Netzwerk codiert werden. Wenn beispielsweise ein Eingabesatz 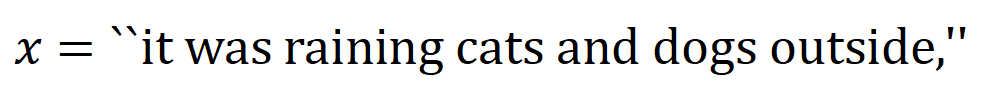 gegeben ist, könnte ein neuronales Netzwerk eine Interaktion zwischen
gegeben ist, könnte ein neuronales Netzwerk eine Interaktion zwischen 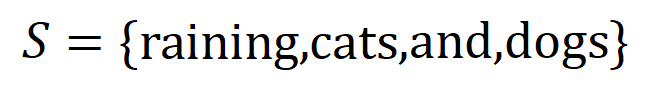 so modellieren, dass
so modellieren, dass 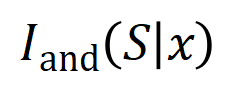 einen numerischen Nutzen erzeugt, der den „Regenguss“ der Ausgabe des neuronalen Netzwerks antreibt. Wenn eine Eingabevariable in
einen numerischen Nutzen erzeugt, der den „Regenguss“ der Ausgabe des neuronalen Netzwerks antreibt. Wenn eine Eingabevariable in 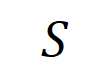 verdeckt ist, wird dieser numerische Nutzen aus der Ausgabe des neuronalen Netzwerks entfernt. In ähnlicher Weise stellt Äquivalenz oder Interaktion
verdeckt ist, wird dieser numerische Nutzen aus der Ausgabe des neuronalen Netzwerks entfernt. In ähnlicher Weise stellt Äquivalenz oder Interaktion 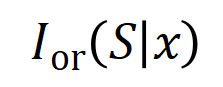 eine „ODER-Beziehung“ zwischen Eingabevariablen innerhalb von
eine „ODER-Beziehung“ zwischen Eingabevariablen innerhalb von  dar, die durch ein neuronales Netzwerk modelliert wird. Wenn beispielsweise ein Eingabesatz
dar, die durch ein neuronales Netzwerk modelliert wird. Wenn beispielsweise ein Eingabesatz 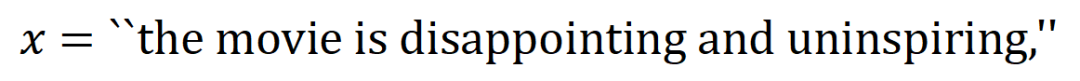 gegeben ist und ein Wort in
gegeben ist und ein Wort in 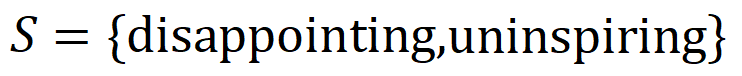 vorkommt, wird die Ausgabe des neuronalen Netzwerks zur Klassifizierung negativer Emotionen gesteuert.
vorkommt, wird die Ausgabe des neuronalen Netzwerks zur Klassifizierung negativer Emotionen gesteuert. 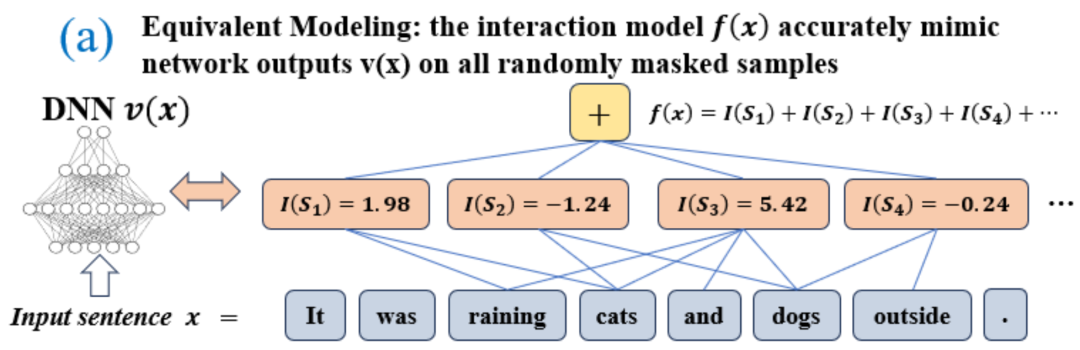
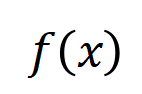 . Jede Interaktion ist ein Maß für die nichtlineare Beziehung zwischen dem neuronalen Netzwerk und der Modellierung eines bestimmten Satzes von Eingabevariablen
. Jede Interaktion ist ein Maß für die nichtlineare Beziehung zwischen dem neuronalen Netzwerk und der Modellierung eines bestimmten Satzes von Eingabevariablen 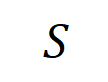 . Wenn und nur wenn die Variablen im Satz gleichzeitig erscheinen, wird sie ausgelöst und interagiert und trägt einen numerischen Wert zur Ausgabe bei
. Wenn und nur wenn die Variablen im Satz gleichzeitig erscheinen, wird sie ausgelöst und interagiert und trägt einen numerischen Wert zur Ausgabe bei 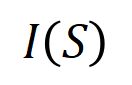 Wenn eine Variable im Satz
Wenn eine Variable im Satz  erscheint, wird sie ausgelöst oder interagiert.
erscheint, wird sie ausgelöst oder interagiert. 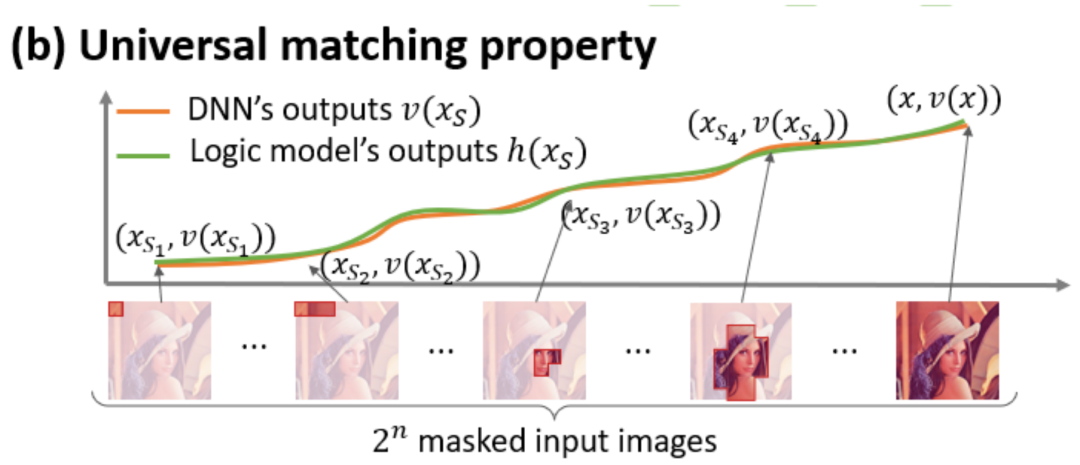
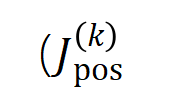 und
und 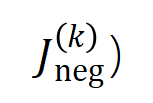 extrahiert aus neuronalen Netzen, die für verschiedene Runden trainiert wurden. Der Trainingsprozess verschiedener neuronaler Netze, die auf unterschiedlichen Datensätzen und unterschiedlichen Aufgaben trainiert werden, weist ein zweistufiges Phänomen auf. Die ersten beiden ausgewählten Zeitpunkte gehören zur ersten Phase, während die letzten beiden Zeitpunkte zur zweiten Phase gehören. Gerade kurz nach Eintritt in die zweite Phase des neuronalen Netztrainingsprozesses beginnt die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust des neuronalen Netzes deutlich anzusteigen (siehe letzte Spalte). Dies zeigt, dass das zweistufige Phänomen des neuronalen Netzwerktrainings zeitlich an Änderungen der Modellverlustlücke „ausgerichtet“ wird. Weitere experimentelle Ergebnisse finden Sie im Artikel.
extrahiert aus neuronalen Netzen, die für verschiedene Runden trainiert wurden. Der Trainingsprozess verschiedener neuronaler Netze, die auf unterschiedlichen Datensätzen und unterschiedlichen Aufgaben trainiert werden, weist ein zweistufiges Phänomen auf. Die ersten beiden ausgewählten Zeitpunkte gehören zur ersten Phase, während die letzten beiden Zeitpunkte zur zweiten Phase gehören. Gerade kurz nach Eintritt in die zweite Phase des neuronalen Netztrainingsprozesses beginnt die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust des neuronalen Netzes deutlich anzusteigen (siehe letzte Spalte). Dies zeigt, dass das zweistufige Phänomen des neuronalen Netzwerktrainings zeitlich an Änderungen der Modellverlustlücke „ausgerichtet“ wird. Weitere experimentelle Ergebnisse finden Sie im Artikel. 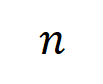 , die
, die  Eingabevariablen enthält,
Eingabevariablen enthält,  die aus der Eingabeprobe
die aus der Eingabeprobe  extrahierten
extrahierten 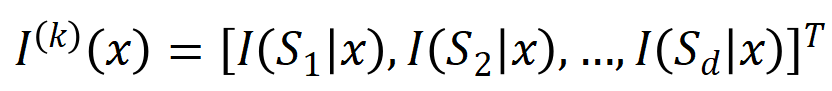 -Ordnungsinteraktionen, wobei
-Ordnungsinteraktionen, wobei 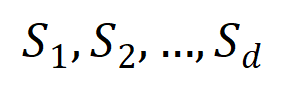
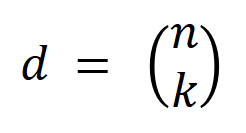
 -Ordnungsinteraktionen darstellt. Anschließend berechnen wir den durchschnittlichen Interaktionsvektor der Ordnung
-Ordnungsinteraktionen darstellt. Anschließend berechnen wir den durchschnittlichen Interaktionsvektor der Ordnung 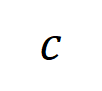 , der aus allen Stichproben mit der Kategorie
, der aus allen Stichproben mit der Kategorie  in der Klassifizierungsaufgabe extrahiert wurde, ausgedrückt als
in der Klassifizierungsaufgabe extrahiert wurde, ausgedrückt als 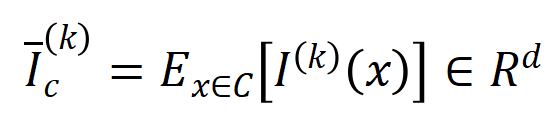 , wobei
, wobei 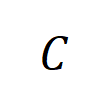 die Menge der Stichproben mit der Kategorie
die Menge der Stichproben mit der Kategorie  darstellt.Als nächstes berechnen wir die Jaccard-Ähnlichkeit zwischen dem durchschnittlichen Interaktionsvektor
darstellt.Als nächstes berechnen wir die Jaccard-Ähnlichkeit zwischen dem durchschnittlichen Interaktionsvektor 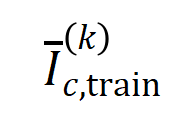 der Ordnung
der Ordnung  , der aus den Trainingsproben extrahiert wurde, und dem durchschnittlichen Interaktionsvektor
, der aus den Trainingsproben extrahiert wurde, und dem durchschnittlichen Interaktionsvektor 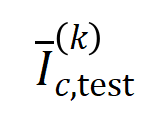 der Ordnung
der Ordnung  , der aus den Testproben extrahiert wurde, um die
, der aus den Testproben extrahiert wurde, um die  der Proben mit der Kategorie
der Proben mit der Kategorie 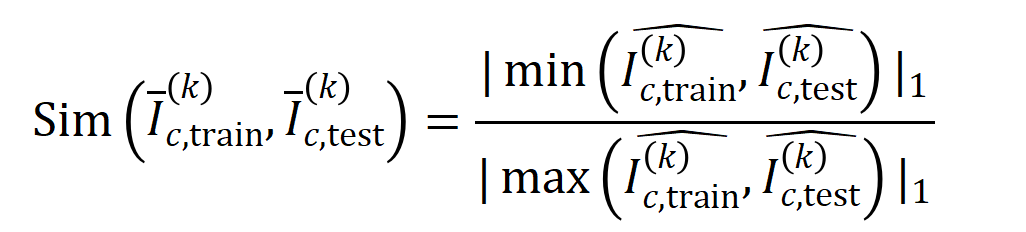
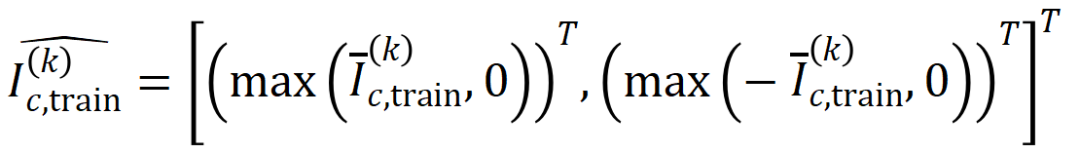 wobei
wobei 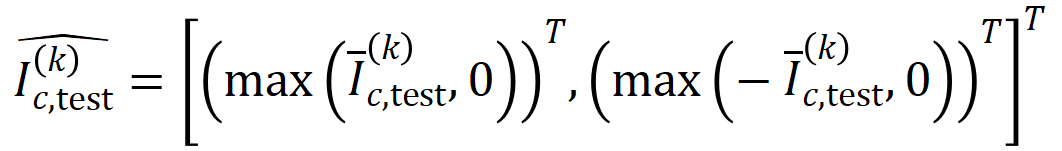 und
und 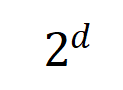 zwei
zwei 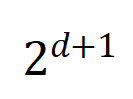 -dimensionale Interaktionsvektoren auf zwei
-dimensionale Interaktionsvektoren auf zwei 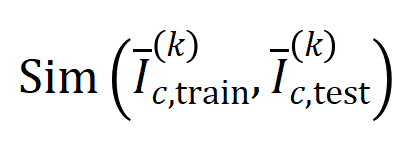 Wir haben Experimente durchgeführt, um verschiedene Bestellinteraktionen zu berechnen
Wir haben Experimente durchgeführt, um verschiedene Bestellinteraktionen zu berechnen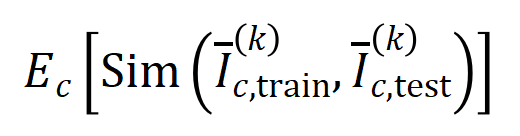 . Wir haben LeNet getestet, das auf dem MNIST-Datensatz trainiert wurde, VGG-11, das auf dem CIFAR-10-Datensatz trainiert wurde, VGG-13, das auf dem CUB200-2011-Datensatz trainiert wurde, und AlexNet, das auf dem Tiny-ImageNet-Datensatz trainiert wurde. Um den Rechenaufwand zu reduzieren, haben wir nur die durchschnittliche Jaccard-Ähnlichkeit der Top-10-Kategorien berechnet
. Wir haben LeNet getestet, das auf dem MNIST-Datensatz trainiert wurde, VGG-11, das auf dem CIFAR-10-Datensatz trainiert wurde, VGG-13, das auf dem CUB200-2011-Datensatz trainiert wurde, und AlexNet, das auf dem Tiny-ImageNet-Datensatz trainiert wurde. Um den Rechenaufwand zu reduzieren, haben wir nur die durchschnittliche Jaccard-Ähnlichkeit der Top-10-Kategorien berechnet
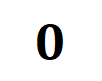
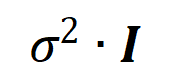
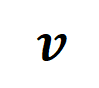 로 특정 샘플에 대한 신경망 추론 을 다시 작성합니다.
로 특정 샘플에 대한 신경망 추론 을 다시 작성합니다.  여기서
여기서  는 만족스러운 스칼라 가중치입니다
는 만족스러운 스칼라 가중치입니다  .
.  기능은 모든 교합 샘플
기능은 모든 교합 샘플  에서
에서  을 만족시키는 대화형 트리거 기능입니다. 함수
을 만족시키는 대화형 트리거 기능입니다. 함수  의 특정 형태는 Taylor 확장에서 파생될 수 있습니다. 논문을 참조하세요. 여기서는 설명하지 않습니다.
의 특정 형태는 Taylor 확장에서 파생될 수 있습니다. 논문을 참조하세요. 여기서는 설명하지 않습니다. 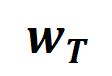 에 대한 학습으로 간주할 수 있습니다. 또한, 실험실의 예비 작업[3]에서는 동일한 작업에 대해 완전히 훈련된 서로 다른 신경망이 유사한 상호 작용을 모델링하는 경향이 있음을 발견했습니다. 따라서 신경망 학습을 일련의 잠재적인 실제 상호 작용으로 간주할 수 있습니다. 따라서 신경망이 수렴하도록 훈련될 때 모델링된 상호 작용은 다음 목적 함수를 최소화할 때 얻은 솔루션으로 볼 수 있습니다.
에 대한 학습으로 간주할 수 있습니다. 또한, 실험실의 예비 작업[3]에서는 동일한 작업에 대해 완전히 훈련된 서로 다른 신경망이 유사한 상호 작용을 모델링하는 경향이 있음을 발견했습니다. 따라서 신경망 학습을 일련의 잠재적인 실제 상호 작용으로 간주할 수 있습니다. 따라서 신경망이 수렴하도록 훈련될 때 모델링된 상호 작용은 다음 목적 함수를 최소화할 때 얻은 솔루션으로 볼 수 있습니다.  여기서
여기서  는 신경망이 적합해야 하는 일련의 잠재적인 Ground Truth 상호 작용을 나타냅니다.
는 신경망이 적합해야 하는 일련의 잠재적인 Ground Truth 상호 작용을 나타냅니다.  과
과 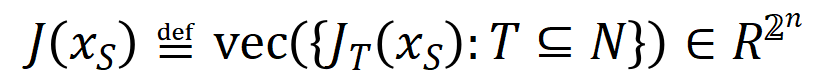 는 각각 모든 가중치를 합친 벡터와 모든 상호작용 트리거 함수의 값을 합친 벡터를 나타냅니다.
는 각각 모든 가중치를 합친 벡터와 모든 상호작용 트리거 함수의 값을 합친 벡터를 나타냅니다. 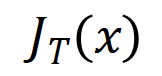
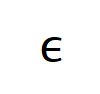 만족되는 곳
만족되는 곳 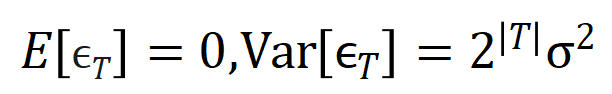 . 그리고 훈련이 진행됨에 따라 노이즈의 분산
. 그리고 훈련이 진행됨에 따라 노이즈의 분산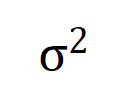 은 점차 작아집니다.
은 점차 작아집니다.  에 대해 위의 손실 함수를 최소화하면 아래 그림의 정리와 같이 최적 상호 작용 가중치
에 대해 위의 손실 함수를 최소화하면 아래 그림의 정리와 같이 최적 상호 작용 가중치  의 분석 솔루션 을 얻을 수 있습니다.
의 분석 솔루션 을 얻을 수 있습니다. 
 가 작아짐), 저차 및 중차 상호 작용 강도 대 고차 상호 작용 강도의 비율이 점차 감소한다는 것을 발견했습니다 (그림에 표시된 대로) 아래 정리). 이는 신경망이 훈련의 두 번째 단계에서 점차적으로 고차 상호작용을 학습하는 현상을 설명합니다.
가 작아짐), 저차 및 중차 상호 작용 강도 대 고차 상호 작용 강도의 비율이 점차 감소한다는 것을 발견했습니다 (그림에 표시된 대로) 아래 정리). 이는 신경망이 훈련의 두 번째 단계에서 점차적으로 고차 상호작용을 학습하는 현상을 설명합니다. 
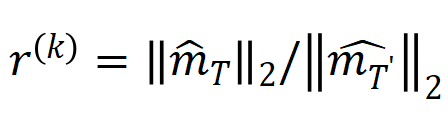 (여기서
(여기서 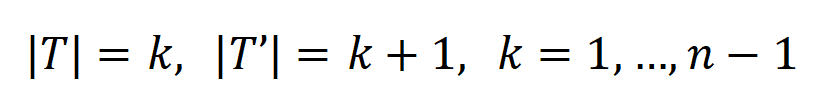 )을 사용하여 k+1차 상호 작용에 대한 k차 상호 작용의 강도 비율을 대략적으로 측정할 수 있습니다. 아래 그림에서 서로 다른 입력 단위 수 n과 서로 다른 차수 k에서
)을 사용하여 k+1차 상호 작용에 대한 k차 상호 작용의 강도 비율을 대략적으로 측정할 수 있습니다. 아래 그림에서 서로 다른 입력 단위 수 n과 서로 다른 차수 k에서  이 감소함에 따라 비율이 점차 감소하는 것을 확인할 수 있습니다.
이 감소함에 따라 비율이 점차 감소하는 것을 확인할 수 있습니다. 
 점차 감소합니다. . 이는 훈련이 진행됨에 따라(즉,
점차 감소합니다. . 이는 훈련이 진행됨에 따라(즉,  점차 작아짐), 저차 상호작용 강도와 고차 상호작용 강도의 비율이 점차 작아지고, 신경망이 점차 고차 상호작용을 학습한다는 것을 보여줍니다. ㅋㅋㅋ 이론 상호작용 분포는 실제 훈련의 각 시점에서의 상호작용 강도 분포를 잘 예측할 수 있습니다.
점차 작아짐), 저차 상호작용 강도와 고차 상호작용 강도의 비율이 점차 작아지고, 신경망이 점차 고차 상호작용을 학습한다는 것을 보여줍니다. ㅋㅋㅋ 이론 상호작용 분포는 실제 훈련의 각 시점에서의 상호작용 강도 분포를 잘 예측할 수 있습니다. 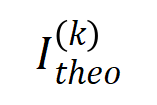 (파란색 히스토그램)과 실제 상호 작용 분포
(파란색 히스토그램)과 실제 상호 작용 분포 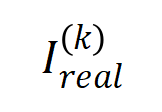 (주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요.
(주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 
 이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다.
이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 
