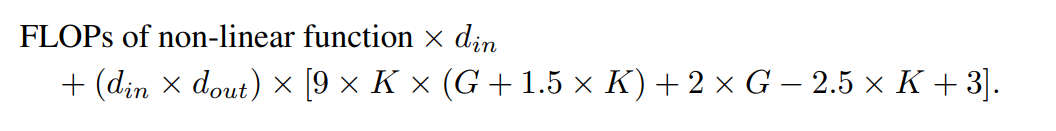KAN ist führend in der symbolischen Darstellung, aber MLP ist immer noch ein Generalist.
Multi-Layer Perceptrons (MLP), auch bekannt als vollständig verbundene Feedforward-Neuronale Netze, sind ein Grundbestandteil der heutigen Deep-Learning-Modelle. Die Bedeutung von MLP kann nicht genug betont werden, da es die Standardmethode zur Approximation nichtlinearer Funktionen beim maschinellen Lernen ist. Allerdings weist MLP auch bestimmte Einschränkungen auf, beispielsweise die Schwierigkeit, die erlernten Darstellungen zu interpretieren, und die Schwierigkeit, die Netzwerkgröße flexibel zu skalieren. Die Entstehung von KAN (Kolmogorov–Arnold Networks) bietet eine innovative Alternative zum traditionellen MLP. Diese Methode übertrifft MLP in Bezug auf Genauigkeit und Interpretierbarkeit und ist in der Lage, MLPs zu übertreffen, die mit viel größeren Parametergrößen und einer sehr kleinen Anzahl von Parametern ausgeführt werden. Die Frage ist also: Welches soll ich zwischen KAN und MLP wählen? Einige Leute unterstützen MLP, weil KAN nur ein gewöhnliches MLP ist und überhaupt nicht ersetzt werden kann, andere glauben, dass KAN überlegen ist. Der aktuelle Vergleich zwischen den beiden beschränkt sich auch auf unterschiedliche Parameter oder FLOPs und die experimentellen Ergebnisse sind unfair. Um das Potenzial von KAN auszuloten, ist es notwendig, KAN und MLP in einem fairen Rahmen umfassend zu vergleichen. Zu diesem Zweck trainierten und bewerteten Forscher der National University of Singapore KAN und MLP in Aufgaben in verschiedenen Bereichen, darunter symbolische Formeldarstellung, maschinelles Lernen, während sie die Parameter oder FLOPs von KAN und MLP Computer Vision kontrollierten. NLP und Audioverarbeitung. Unter diesen fairen Bedingungen stellten sie fest, dass KAN MLP nur bei der symbolischen Formeldarstellungsaufgabe übertraf, während MLP KAN bei anderen Aufgaben im Allgemeinen übertraf.
- Papieradresse: https://arxiv.org/pdf/2407.16674
- Projektlink: https://github.com/yu-rp/KANbeFair
- Papiertitel: KAN oder MLP: Ein fairerer Vergleich
Der Autor stellte außerdem fest, dass der Vorteil von KAN bei der symbolischen Formeldarstellung auf der Verwendung der B-Spline-Aktivierungsfunktion beruht. Anfangs blieb die Gesamtleistung von MLP hinter der von KAN zurück, aber nachdem die Aktivierungsfunktion von MLP durch B-Splines ersetzt wurde, erreichte die Leistung die Leistung von KAN oder übertraf sie sogar. Allerdings können B-Splines die Leistung von MLP bei anderen Aufgaben wie Computer Vision nicht weiter verbessern. Die Autoren fanden außerdem heraus, dass KAN bei kontinuierlichen Lernaufgaben tatsächlich nicht besser abschneidet als MLP. Das ursprüngliche KAN-Papier verglich die Leistung von KAN und MLP bei einer kontinuierlichen Lernaufgabe unter Verwendung einer Reihe eindimensionaler Funktionen, wobei jede nachfolgende Funktion eine Übersetzung der vorherigen Funktion entlang der Zahlenachse ist. In diesem Artikel wird die Leistung von KAN und MLP in einer Standardumgebung für klasseninkrementelles kontinuierliches Lernen verglichen. Unter festen Trainingsiterationsbedingungen stellten sie fest, dass das Vergessensproblem von KAN schwerwiegender war als das von MLP. KAN, MLP kurze EinführungKAN hat zwei Zweige, der erste Zweig ist der B-Spline-Zweig und der andere Zweig ist der Shortcut-Zweig, dh nichtlineare Aktivierung und lineare Transformation miteinander verbunden. In der offiziellen Implementierung ist der Shortcut-Zweig eine SiLU-Funktion, gefolgt von einer linearen Transformation. x sei der Merkmalsvektor einer Probe. Dann kann die Vorwärtsgleichung des KAN-Spline-Zweigs wie folgt geschrieben werden: In der ursprünglichen KAN-Architektur wird die Spline-Funktion als B-Spline-Funktion gewählt. Die Parameter jeder B-Spline-Funktion werden zusammen mit den anderen Netzwerkparametern gelernt. Entsprechend kann die Vorwärtsgleichung des einschichtigen MLP wie folgt ausgedrückt werden: Diese Formel hat die gleiche Form wie die B-Spline-Verzweigungsformel in KAN, unterscheidet sich jedoch in der nichtlinearen Funktion . Daher kann KAN unabhängig von der Interpretation der KAN-Struktur im Originalpapier auch als vollständig verbundene Schicht betrachtet werden. Daher gibt es zwei Hauptunterschiede zwischen KAN und gewöhnlichem MLP:
- Die Aktivierungsfunktion ist unterschiedlich. Normalerweise umfasst die Aktivierungsfunktion in MLP ReLU, GELU usw., die keine lernbaren Parameter haben und für alle Eingabeelemente einheitlich sind. In KAN ist die Aktivierungsfunktion eine Spline-Funktion mit lernbaren Parametern und für jede Eingabe Die Elemente sind alle unterschiedlich .
- Abfolge linearer und nichtlinearer Operationen.Im Allgemeinen werden Forscher sich MLP so vorstellen, dass es zunächst eine lineare Transformation und dann eine nichtlineare Transformation durchführt, während KAN tatsächlich zuerst eine nichtlineare Transformation und dann eine lineare Transformation durchführt. Bis zu einem gewissen Grad ist es aber auch möglich, die vollständig verbundenen Schichten in MLP zunächst als nichtlinear und dann als linear zu beschreiben.
Durch den Vergleich von KAN und MLP geht diese Studie davon aus, dass der Unterschied zwischen den beiden hauptsächlich in der Aktivierungsfunktion liegt. Daher stellten sie die Hypothese auf, dass Unterschiede in den Aktivierungsfunktionen KAN und MLP für unterschiedliche Aufgaben geeignet machen, was zu funktionalen Unterschieden zwischen den beiden Modellen führt. Um diese Hypothese zu testen, verglichen die Forscher die Leistung von KAN und MLP bei verschiedenen Aufgaben und beschrieben, für welche Aufgaben jedes Modell geeignet ist. Um einen fairen Vergleich zu gewährleisten, wurden in der Studie zunächst Formeln zur Berechnung der Anzahl der Parameter und FLOPs von KAN und MLP abgeleitet. Der experimentelle Prozess steuert die gleiche Anzahl von Parametern oder FLOPs, um die Leistung von KAN und MLP zu vergleichen. Die Anzahl der Parameter von 的KAN und MLP und die Anzahl der Steuerparameter im FLOP Kan kann Parameter lernen, einschließlich Kontrollpunkte der Größe B, Verknüpfungsgewichte und B-Größe Gewichtsgewichte und Bias-Term. Die Gesamtzahl der lernbaren Parameter beträgt: wobei d_in und d_out die Eingabe- und Ausgabedimensionen der neuronalen Netzwerkschicht darstellen, K die Reihenfolge des Splines darstellt, die dem Parameter k des offiziellen nn.Module entspricht KANLayer, die Ordnung der Polynombasis in der Spline-Funktion. G stellt die Anzahl der Spline-Intervalle dar, was dem num-Parameter des offiziellen nn.Module KANLayer entspricht. Dies ist die Anzahl der Intervalle des B-Splines vor dem Füllen. Vor dem Füllen entspricht die Anzahl der Kontrollpunkte 1. Nach dem Füllen sollten (K + G) gültige Kontrollpunkte vorhanden sein.
Entsprechend sind die lernbaren Parameter einer MLP-Schicht:
In der Bewertung des Autors wird der FLOP jeder arithmetischen Operation als 1 angesehen, Der FLOP boolescher Operationen wird als 0 betrachtet. Die Operationen 0. Ordnung im De Boor-Cox-Algorithmus können in eine Reihe boolescher Operationen umgewandelt werden, die keine Gleitkommaoperationen erfordern. Daher ist sein FLOP theoretisch 0. Dies unterscheidet sich von der offiziellen KAN-Implementierung, bei der boolesche Daten für Operationen wieder in Gleitkommadaten konvertiert werden. In der Bewertung des Autors wird FLOP für eine Probe berechnet. Der mithilfe der De Boor-Cox-Iterationsformel im offiziellen KAN-Code implementierte B-Spline-FLOP lautet:
Zusammen mit dem FLOP des Abkürzungspfads und dem FLOP der Zusammenführung der beiden Zweige ergibt sich der Gesamt-FLOP einer KAN-Schicht ist:
Entsprechend ist der FLOP einer MLP-Schicht:
Die FLOP-Differenz zwischen der KAN-Schicht und der MLP-Schicht mit derselben Eingabedimension und Ausgabedimension kann ausgedrückt werden als:
Wenn der MLP auch zuerst nichtlineare Operationen ausführt, ist der führende Term Null.
Das Ziel des Autors ist es, die Leistungsunterschiede zwischen KAN und MLP zu vergleichen, wenn die Anzahl der Parameter oder FLOPs gleich ist. Das Experiment deckt mehrere Bereiche ab, darunter maschinelles Lernen, Computer Vision, Verarbeitung natürlicher Sprache, Audioverarbeitung und symbolische Formeldarstellung. Alle Experimente verwendeten den Adam-Optimierer und wurden alle auf einer RTX3090-GPU durchgeführt. Maschinelles Lernen. Die Autoren führten Experimente mit 8 Datensätzen für maschinelles Lernen durch, wobei sie KAN und MLP mit einer oder zwei verborgenen Schichten verwendeten, und passten basierend auf den Eigenschaften jedes Datensatzes die Eingabe- und Ausgabedimensionen des neuronalen Netzwerks an. Für MLP ist die Breite der verborgenen Schicht auf 32, 64, 128, 256, 512 oder 1024 eingestellt und GELU oder ReLU wird als Aktivierungsfunktion verwendet, während in MLP eine Normalisierungsschicht verwendet wird. Für KAN beträgt die Breite der verborgenen Schicht 2, 4, 8 oder 16, die Anzahl der B-Spline-Netze beträgt 3, 5, 10 oder 20 und der B-Spline-Grad beträgt 2, 3 oder 5.
Da die ursprüngliche KAN-Architektur keine Normalisierungsschicht enthält, hat der Autor den Wertebereich der KAN-Spline-Funktion erweitert, um die möglichen Vorteile der Normalisierungsschicht in MLP auszugleichen. Alle Experimente wurden über 20 Trainingsrunden durchgeführt und die beste Genauigkeit, die mit dem Testsatz während des Trainingsprozesses erreicht wurde, wurde aufgezeichnet, wie in den Abbildungen 2 und 3 dargestellt. Bei Datensätzen für maschinelles Lernen behält MLP normalerweise einen Vorteil. In ihren Experimenten mit acht Datensätzen übertraf MLP KAN bei sechs davon. Sie stellten jedoch auch fest, dass die Leistung von MLP und KAN bei einem Datensatz nahezu gleich war, während KAN beim anderen Datensatz eine bessere Leistung als MLP erbrachte. Insgesamt hat MLP immer noch allgemeine Vorteile bei Datensätzen für maschinelles Lernen. Computer Vision. Die Autoren führten Experimente mit 8 Computer-Vision-Datensätzen durch. Sie verwendeten KANs und MLPs mit einer oder zwei verborgenen Schichten und passten die Eingabe- und Ausgabedimensionen des neuronalen Netzwerks je nach Datensatz an. In Computer-Vision-Datensätzen hat die durch die Spline-Funktion von KAN eingeführte Verarbeitungsverzerrung keine Auswirkung und ihre Leistung ist der von MLP mit der gleichen Anzahl von Parametern oder FLOPs immer unterlegen. Audio- und natürliche Sprachverarbeitung. Die Autoren führten Experimente mit zwei Audioklassifizierungs- und zwei Textklassifizierungsdatensätzen durch. Sie verwendeten KAN und MLP mit ein bis zwei verborgenen Schichten und passten die Eingabe- und Ausgabedimensionen des neuronalen Netzwerks entsprechend den Eigenschaften des Datensatzes an. Bei beiden Audiodatensätzen übertrifft MLP KAN. Bei der Textklassifizierungsaufgabe behält MLP seinen Vorsprung gegenüber dem AG News-Datensatz. Im CoLA-Datensatz gibt es jedoch keinen signifikanten Leistungsunterschied zwischen MLP und KAN. KAN scheint gegenüber dem CoLA-Datensatz im Vorteil zu sein, wenn die Anzahl der Steuerparameter gleich ist. Da die Splines von KAN jedoch einen höheren FLOP erfordern, ist dieser Vorteil in Experimenten mit kontrolliertem FLOP nicht durchgängig erkennbar. Bei der Kontrolle von FLOP scheint MLP überlegen zu sein. Daher Es gibt keine klare Antwort darauf, welches Modell im CoLA-Datensatz besser ist. Insgesamt ist MLP sowohl bei Audio- als auch bei Textaufgaben immer noch die bessere Wahl. Symbolformeldarstellung. Die Autoren verglichen die Unterschiede zwischen KAN und MLP anhand von acht symbolischen Formeldarstellungsaufgaben. Sie verwendeten KAN und MLP mit einer bis vier verborgenen Schichten und passten die Eingabe- und Ausgabedimensionen des neuronalen Netzwerks entsprechend dem Datensatz an. KAN übertrifft MLP bei 7 von 8 Datensätzen und kontrolliert gleichzeitig die Anzahl der Parameter. Bei der Steuerung für FLOP ist die Leistung von KAN in etwa gleichauf mit MLP, übertrifft MLP bei zwei Datensätzen und ist MLP auf der anderen Seite aufgrund der zusätzlichen Rechenkomplexität, die durch Splines entsteht, unterlegen. Insgesamt übertrifft KAN MLP bei der Aufgabe der symbolischen Formeldarstellung. Das obige ist der detaillierte Inhalt vonUmgedreht? In einem neuen Wettbewerb gewann KAN, das behauptet, MLP zu ersetzen, nur ein Spiel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Stellungnahme:Der Inhalt dieses Artikels wird freiwillig von Internetnutzern beigesteuert und das Urheberrecht liegt beim ursprünglichen Autor. Diese Website übernimmt keine entsprechende rechtliche Verantwortung. Wenn Sie Inhalte finden, bei denen der Verdacht eines Plagiats oder einer Rechtsverletzung besteht, wenden Sie sich bitte an admin@php.cn