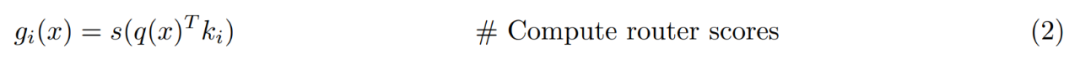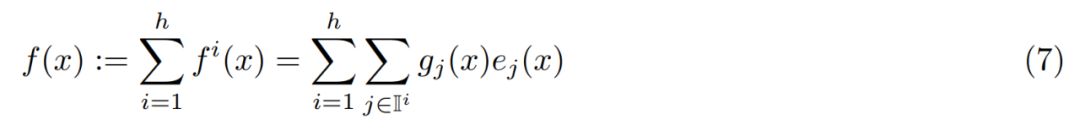Als Einzelautor schlägt Google Millionen von Expertenmischungen vor, die dichtes Feedforward und spärliches MoE übertreffen

Entfesseln Sie das Potenzial, Transformer weiter zu skalieren und gleichzeitig die Recheneffizienz beizubehalten.

Feedforward (FFW)-Schichten in der Standard-Transformer-Architektur führen zu einem linearen Anstieg der Rechenkosten und des Aktivierungsspeichers, wenn die Breite der verborgenen Schicht zunimmt. Da die Größe großer Sprachmodelle (LLM) weiter zunimmt, ist die Sparse Mixed Expert (MoE)-Architektur zu einer praktikablen Methode zur Lösung dieses Problems geworden, die die Modellgröße vom Rechenaufwand trennt. Viele neue MoE-Modelle können bei gleicher Größe eine bessere Leistung und eine höhere Leistung erzielen.

Das kürzlich entdeckte feinkörnige MoE-Erweiterungsgesetz zeigt, dass eine höhere Granularität zu einer besseren Leistung führt. Allerdings sind bestehende MoE-Modelle aufgrund von Rechen- und Optimierungsherausforderungen auf eine geringe Anzahl von Experten beschränkt.

Diesen Dienstag, Neue Forschung von Google DeepMind stellt einen Parameter-effizienten Expertenabrufmechanismus vor, der Produktschlüsseltechnologie nutzt, um eine spärliche Abfrage von einer Million Mikroexperten durchzuführen.

Link: https://arxiv.org/abs/2407.04153

Dieser Ansatz versucht, den Rechenaufwand von der Parameteranzahl zu entkoppeln, indem er durch eine erlernte Indexstruktur effizient eine große Anzahl kleiner Experten verkettet Routenführung. Zeigt eine überlegene Effizienz im Vergleich zu dichten FFW-, grobkörnigen MoE- und Product Key Memory (PKM)-Schichten.

Diese Arbeit stellt die Parameter Efficient Expert Retrieval (PEER)-Architektur (Parameter Efficient Expert Retrieval) vor, die den Produktschlüsselabruf nutzt, um effizient an eine große Anzahl von Experten weiterzuleiten und dabei den Rechenaufwand von der Menge der Parameter zu trennen. Dieses Design zeigte in Experimenten eine überlegene Rechenleistung und positionierte es als wettbewerbsfähige Alternative zu dichten FFW-Schichten zur Erweiterung von Basismodellen. Die Hauptbeiträge dieser Arbeit sind:

Erforschung extremer MoE-Einstellungen: Im Gegensatz zur Fokussierung auf einige wenige große Experten in früheren MoE-Studien untersucht diese Arbeit die wenig erforschte Situation zahlreicher kleiner Experten.

Erlernte Indexstruktur für das Routing: Erster Beweis dafür, dass eine erlernte Indexstruktur effizient an über eine Million Experten weitergeleitet werden kann.

Neues Layer-Design: Durch die Kombination von Produktschlüsselrouting mit Einzelneuron-Experten führen wir den PEER-Layer ein, der die Layer-Kapazität ohne nennenswerten Rechenaufwand skaliert. Empirische Ergebnisse zeigen eine höhere Effizienz im Vergleich zu dichten FFW-, grobkörnigen MoE- und Product Key Memory (PKM)-Schichten.

Umfassende Ablationsstudie: Wir untersuchen die Auswirkungen verschiedener Designentscheidungen für PEER (z. B. Anzahl der Experten, Aktivitätsparameter, Anzahl der Köpfe und Abfragebatch-Normalisierung) auf Sprachmodellierungsaufgaben.

Einführung in die Methode

In diesem Abschnitt erklärt der Forscher ausführlich die PEER-Schicht (Parametric Efficient Expert Retrieval), eine hybride Expertenarchitektur, die Produktschlüssel beim Routing und Single-Neuron-MLP als verwendet Experte. Abbildung 2 unten zeigt den Berechnungsprozess innerhalb der PEER-Schicht.

Übersicht über die PEER-Ebene. Formal ist die PEER-Schicht eine Funktion f : R^n → R^m, die aus drei Teilen besteht: einem Pool von N Experten E := {e_i}^N_i=1, wobei jeder Experte e_i : R^n → R ist ^m hat die gleiche Signatur wie f; einen entsprechenden Satz von N Produktschlüsseln K := {k_i}^N_i=1 ⊂ R^d; und ein Abfragenetzwerk q : R^n → R ^d, das den Eingabevektor abbildet x ∈ R^n zum Abfragevektor q (x).

T_k sei der Top-k-Operator. Rufen Sie bei einer gegebenen Eingabe x zunächst eine Teilmenge von k Experten ab, deren entsprechende Produktschlüssel das höchste innere Produkt mit der Abfrage q (x) haben.

Wenden Sie dann eine nichtlineare Aktivierung (z. B. Softmax oder Sigmoid) auf das innere Produkt des Abfrageschlüssels der Top-k-Experten an, um den Routing-Score zu erhalten.

Abschließend wird die Ausgabe berechnet, indem die Expertenausgaben gewichtet nach Routing-Scores linear kombiniert werden.

Produktschlüsselabruf. Da die Forscher beabsichtigen, eine große Anzahl von Experten einzusetzen (N ≥ 10^6), kann die einfache Berechnung der Top-k-Indizes in Gleichung 1 sehr kostspielig sein, weshalb die Technik zum Abrufen von Produktschlüsseln angewendet wird. Anstatt N unabhängige d-dimensionale Vektoren als Schlüssel k_i zu verwenden, erstellen sie diese durch Verketten von Vektoren aus zwei unabhängigen d/2-dimensionalen Unterschlüsselsätzen (d. h. C, C ′ ⊂ R d/2):

Parametrisch effiziente Experten- und Mehrkopfsuche. Im Gegensatz zu anderen MoE-Architekturen legen diese Architekturen die verborgene Ebene jedes Experten normalerweise auf die gleiche Größe wie andere FFW-Ebenen fest. In PEER ist jeder Experte e_i ein Singleton-MLP, mit anderen Worten, er hat nur eine verborgene Schicht mit einem einzelnen Neuron:

Die Forscher haben die Größe des einzelnen Experten nicht geändert, sondern Multi-Head-Retrieval verwendet Wird verwendet, um die Ausdrucksfähigkeit der PEER-Schicht anzupassen, die dem Multi-Head-Aufmerksamkeitsmechanismus im Transformer und dem Multi-Head-Speicher in PKM ähnelt.

Konkret verwenden sie h unabhängige Abfragenetzwerke. Jedes Netzwerk berechnet seine eigene Abfrage und ruft einen separaten Satz von k Experten ab. Verschiedene Köpfe teilen sich jedoch denselben Expertenpool mit demselben Satz an Produktschlüsseln. Die Ausgabe dieser h-Köpfe lässt sich einfach wie folgt zusammenfassen:

Warum brauchen wir eine große Anzahl kleiner Experten ? Eine gegebene MoE-Schicht kann durch drei Hyperparameter charakterisiert werden: die Gesamtzahl der Parameter P, die Zahl der aktiven Parameter pro Token P_active und die Größe eines einzelnen Experten P_expert. Krajewski et al. (2024) zeigten, dass das Skalierungsgesetz des MoE-Modells die folgende Form hat:

Für PEER verwendet der Forscher die kleinstmögliche Expertengröße, indem er d_expert = 1 setzt, und die Anzahl der aktivierten Neuronen beträgt Die Anzahl der Suchköpfe wird mit der Anzahl der pro Kopf gefundenen Experten multipliziert: d_active = hk. Daher ist die Granularität von PEER immer G = P_active/P_expert = d_active/d_expert = hk.

Experimentelle Ergebnisse

Sehen wir uns zunächst die Auswertungsergebnisse des Sprachmodellierungsdatensatzes an.

Nachdem die Forscher das rechnerisch optimale Modell für jede Methode auf der Grundlage der isoFLOP-Kurve ermittelt hatten, bewerteten sie die Leistung dieser vorab trainierten Modelle anhand der folgenden gängigen Sprachmodellierungsdatensätze:

• Curation Corpus
• Lambada
• Pile
• Wikitext
• Pre-Training-Datensatz C4

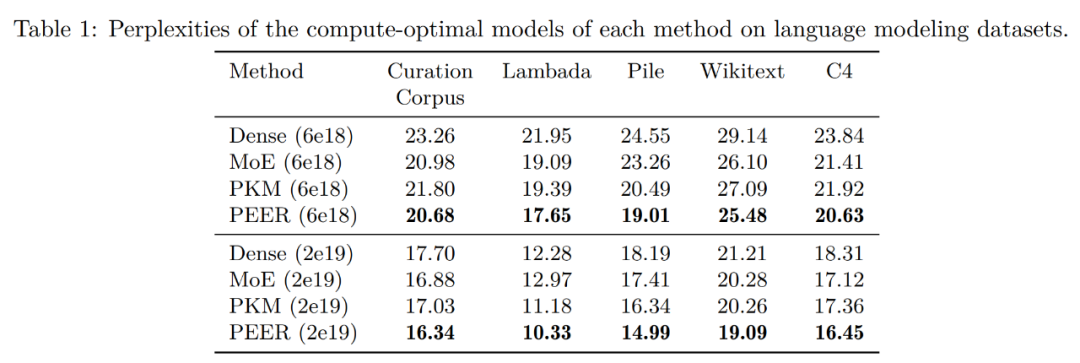
Tabelle 1 unten zeigt die Bewertungsergebnisse. Die Forscher gruppierten die Modelle basierend auf dem FLOP-Budget, das während des Trainings verwendet wurde. Wie man sehen kann, weist PEER bei diesen Sprachmodellierungsdatensätzen die geringste Verwirrung auf.

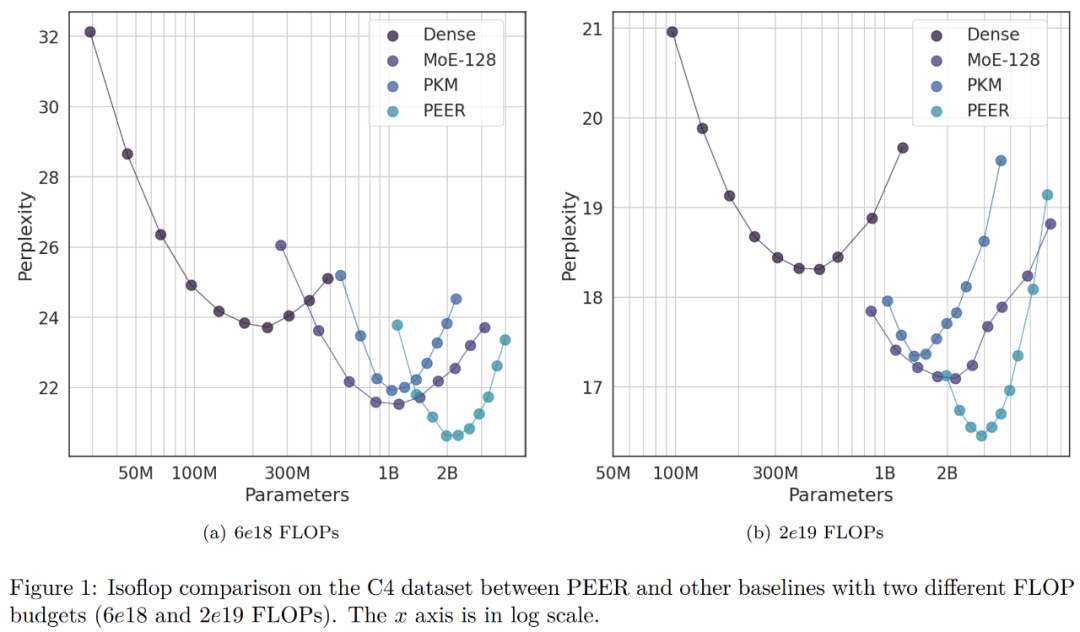
Im Ablationsexperiment veränderten die Forscher die Gesamtzahl der Experten. Die in der isoFLOP-Kurve in Abbildung 1 unten gezeigten Modelle haben alle über eine Million (1024^2) Experten.

Der Forscher wählte das Modell mit der optimalen Position von isoFLOP und änderte die Anzahl der Experten in der PEER-Schicht (N = 128^2, 256^2, 512^2, 1024^2), während die Anzahl der aktiven Experten unverändert blieb (h = 8, k = 16). Die Ergebnisse sind in Abbildung 3(a) unten dargestellt.

Es ist ersichtlich, dass die isoFLOP-Kurve zwischen dem PEER-Modell mit 1024^2 Experten und dem entsprechenden dichten Backbone interpoliert, ohne die FFW-Schicht im Mittelblock durch eine PEER-Schicht zu ersetzen. Dies zeigt, dass die Modellleistung allein durch eine Erhöhung der Expertenzahl verbessert werden kann.

Gleichzeitig änderten die Forscher die Anzahl der aktiven Experten. Sie variierten systematisch die Anzahl der aktiven Experten (hk = 32, 64, 128, 256, 512), während die Gesamtzahl der Experten konstant blieb (N = 1024^2). Für ein gegebenes hk ändert der Forscher dann gemeinsam h und k, um die beste Kombination zu ermitteln. Abbildung 3 (b) unten zeigt die isoFLOP-Kurve in Bezug auf die Anzahl der Köpfe (h).

Tabelle 2 unten listet die Expertennutzung und Ungleichmäßigkeit für unterschiedliche Anzahlen von Experten mit und ohne BN auf. Es ist ersichtlich, dass selbst bei 1 Mio. Experten die Expertenauslastungsrate nahezu 100 % beträgt und die Verwendung von BN die Expertenauslastungsrate ausgewogener und den Grad der Verwirrung verringern kann. Diese Ergebnisse zeigen die Wirksamkeit des PEER-Modells bei der Einbindung einer großen Anzahl von Experten.

Die Forscher verglichen auch die isoFLOP-Kurven mit und ohne BN. Abbildung 4 unten zeigt, dass PEER-Modelle mit BN im Allgemeinen eine geringere Ratlosigkeit erreichen können. Obwohl der Unterschied nicht signifikant ist, macht er sich am deutlichsten in der Nähe des optimalen isoFLOP-Bereichs bemerkbar.

Vorstellung des Autors

Die PEER-Studie hat nur einen Autor, Xu He (Owen), der wissenschaftlicher Mitarbeiter bei Google DeepMind ist und 2017 an der Universität Groningen in den Niederlanden promovierte .

Das obige ist der detaillierte Inhalt vonAls Einzelautor schlägt Google Millionen von Expertenmischungen vor, die dichtes Feedforward und spärliches MoE übertreffen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!