Vorhersage zeitdiskreter Bifurkationen durch Deep Learning

Herausgeber |. Kohlblätter
Viele natürliche und vom Menschen geschaffene Systeme sind anfällig für kritische Übergänge – plötzliche und potenziell schädliche Veränderungen in der Dynamik. Deep-Learning-Klassifikatoren können Frühwarnsignale für kritische Übergänge liefern, indem sie gemeinsame Merkmale von Bifurkationen aus großen simulierten Trainingsdatensätzen lernen. Bisher wurden Klassifikatoren nur darauf trainiert, zeitkontinuierliche Bifurkationen vorherzusagen, wobei die reichhaltige Dynamik ignoriert wurde, die zeitdiskrete Bifurkationen charakterisiert.
Hier trainierte das Forschungsteam von Thomas M. Bury an der McGill University einen Deep-Learning-Klassifikator, um Frühwarnsignale für fünf lokale zeitdiskrete Bifurkationen der Kodimension eins bereitzustellen. Sie testeten den Klassifikator anhand simulierter Daten aus zeitdiskreten Modellen, die in der Physiologie, Ökonomie und Ökologie verwendet werden, sowie experimentellen Daten von spontan schlagenden Hühnerherzaggregaten, die eine periodenverdoppelnde Bifurkation durchlaufen.
Der Klassifikator weist bei verschiedenen Lärmintensitäten und engen Bifurkationsraten eine höhere Empfindlichkeit und Spezifität auf als üblicherweise verwendete Frühwarnsignale. In den meisten Fällen kann es auch die korrekte Bifurkation vorhersagen, mit besonders hoher Genauigkeit für periodenverdoppelnde Bifurkationen, Neimark-Sacker-Bifurkationen und Faltungsbifurkationen.
Die Forschung trug den Titel „Predicting discrete-time bifurcations with deep learning“ und wurde am 10. Oktober 2023 in „Nature Communications“ veröffentlicht.

Kritische Übergänge und Frühwarnsignale (EWS)

1. Kritische Übergänge:
2. Die kritische Schwelle, bei der ein System plötzliche, signifikante dynamische Änderungen erfährt.
3. Zum Beispiel: Herzrhythmusstörungen, Finanzmarktkollaps, Ökosystemkollaps.
4. Bifurkationstheorie:
5. Untersuchung dynamischer Systeme, die an Schwellenwerten qualitative Veränderungen erfahren.
6. Begleitet von einer Schwächung (Verlangsamung) der lokalen Stabilität, was zu Änderungen in den Eigenschaften der Rauschzeitreihen führt.
7. Diese Änderungen sind für kritische Übergänge von EWS verfügbar.
8. Vorhandenes EWS:
9. Varianz- und Lag-1-Autokorrelationsänderungen vor Übergängen in klimatischen, geologischen, ökologischen und kardialen Systemen.
10. Die Vorhersagefähigkeiten sind begrenzt und können in einigen Systemen fehlschlagen.
11. Deep Learning EWS:
12. Trainieren Sie ein neuronales Netzwerk, um Bifurkationstypen basierend auf Zeitreihen vorherzusagen.
13. Lernen Sie universelle Funktionen aus Datenbanken mit gegabelten Simulationen.
14. Aufgrund der universellen Eigenschaften der Bifurkation für unsichtbare Zeitreihen geeignet.

Zeitdiskrete gegabelte EWS

• Zeitdiskrete dynamische Systeme zeigen ein anderes Verhalten als zeitkontinuierliche dynamische Systeme.
• Diskrete Zeitverzweigungen kommen auf natürliche Weise in der Physiologie, Epidemiologie und Ökonomie vor.
• Die Forscher testeten die Leistung von Deep-Learning-Klassifikatoren in zeitdiskreten Bifurkationen anhand simulierter und experimenteller Daten.

Periodische Verdoppelungsgabelung:

• Art der zeitdiskreten Gabelung, bei der Ereignisse abwechselnd in Intervallen auftreten.
• Zusammen mit der Verlangsamung kommt es zu systematischen Veränderungen der Varianz und der Lag-1-Autokorrelation.
• Wurde experimentell in Hühnerherzaggregaten und in menschlichen Herzen beobachtet und kann in EWS verwendet werden.

  

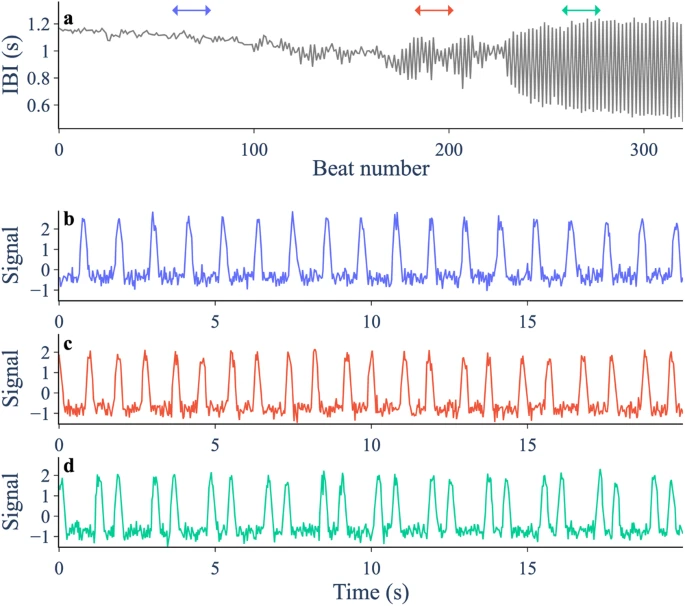
  Abbildung: Nach der Behandlung mit einem Kaliumkanalblocker (E-4031, 1,5 μmol) zeigen spontan schlagende embryonale Hühnerherzzellaggregate eine periodenverdoppelnde Bifurkation. (Quelle: Papier)

Zeitdiskrete Bifurkation

Es gibt viele Arten von zeitdiskreten Bifurkationen, jede mit damit verbundenen dynamischen Änderungen. In der neuesten Studie konzentrierte sich das Bury-Team auf fünf lokale Verzweigungen der Kodimension eins. Im „lokalen“ Fall gehen diese Gabelungen mit starken Verlangsamungen einher, sodass systematische Variation, Varianz und Autokorrelation zu erwarten sind.

Arten vorhergesagter Bifurkationen

Allerdings führen nicht alle dieser Abweichungen zu kritischen Übergängen. Stattdessen können sie fließend in sich überschneidende stationäre Zustände (transkritisch) oder in Schwingungen mit allmählich zunehmender Amplitude (überkritisches Neimark-Sakr) übergehen. Die Vorhersage des Bifurkationstyps liefert Informationen über die Art der Dynamik nach der Bifurkation, die Varianz und Autokorrelation allein nicht liefern können.

Deep-Learning-Klassifikator

Das Team trainiert einen Deep-Learning-Klassifikator, um spezifische EWS für Bifurkationen zeitdiskreter dynamischer Systeme bereitzustellen. Sie trainierten den Klassifikator mithilfe simulierter Daten aus normalisierten Gleichungen, an die Terme höherer Ordnung und Rauschen angehängt waren.

Klassifikatortests

Das Team testete den Klassifikator dann anhand simulierter Läufe von fünf diskreten Zeitmodellen, die in der Kardiologie, Ökologie und Ökonomie verwendet werden, und bewertete seine relative Varianz und die Autokorrelationsleistung von Lag 1. Die Robustheit des EWS wird durch Variation der Geräuschamplitude und der Antriebsrate in Modellsimulationen bewertet.

Experimentelle Validierung

Abschließend testeten die Forscher den Klassifikator anhand experimenteller Daten von spontan schlagenden Hühnerherzaggregaten, die eine periodenverdoppelnde Bifurkation durchliefen.

Papierlink:

https://www.nature.com/articles/s41467-023-42020-z

Das obige ist der detaillierte Inhalt vonVorhersage zeitdiskreter Bifurkationen durch Deep Learning. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!