Die AIxiv-Kolumne ist eine Kolumne, in der diese Website akademische und technische Inhalte veröffentlicht. In den letzten Jahren sind in der AIxiv-Kolumne dieser Website mehr als 2.000 Berichte eingegangen, die Spitzenlabore großer Universitäten und Unternehmen auf der ganzen Welt abdecken und so den akademischen Austausch und die Verbreitung wirksam fördern. Wenn Sie hervorragende Arbeiten haben, die Sie teilen möchten, können Sie gerne einen Beitrag leisten oder uns für die Berichterstattung kontaktieren. E-Mail-Adresse für die Einreichung: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
Die Autoren dieses Artikels stammen aus dem Noah's Ark Laboratory von Huawei in Montreal, Kang Jikun, Li Xinze, Chen Xi, Amirreza Kazemi und Chen Boxing. Künstliche Intelligenz (KI) hat im letzten Jahrzehnt große Fortschritte gemacht, insbesondere in den Bereichen natürliche Sprachverarbeitung und Computer Vision. Es bleibt jedoch eine große Herausforderung, die kognitiven Fähigkeiten und das Denkvermögen der KI zu verbessern. Kürzlich wurde in einem Artikel mit dem Titel „MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time“ eine auf Baumsuche basierende Methode zur Verbesserung der Inferenzzeitfähigkeit MindStar [1] vorgeschlagen, die im Open-Source-Modell Llama implementiert ist -13-B und Mistral-7B haben die Argumentationsfähigkeiten der ungefähren Closed-Source-Großmodelle GPT-3.5 und Grok-1 für mathematische Probleme erreicht. 
- Papiertitel: MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time
- Papieradresse: https://arxiv.org/abs/2405.16265v2
MindStar Anwendungseffekt auf mathematische Fragestellungen: 
Abbildung 1: Mathematische Genauigkeit verschiedener groß angelegter Sprachmodelle. LLaMA-2-13B ähnelt in der mathematischen Leistung GPT-3.5 (4-Schuss), spart jedoch etwa 200-mal mehr Rechenressourcen. Einleitung Beeindruckende Ergebnisse wurden in Bereichen wie , und kreativem Schreiben gezeigt [5]. Es bleibt jedoch eine Herausforderung, die Fähigkeit von LLMs zur Lösung komplexer Denkaufgaben freizuschalten. Einige neuere Studien [6,7] versuchen, das Problem durch Supervised Fine-Tuning (SFT) zu lösen, indem sie neue Inferenzdatenproben mit dem Originaldatensatz mischen. LLMs lernen die zugrunde liegende Verteilung dieser Proben und versuchen, die zugrunde liegende Verteilung zu imitieren. Lernen Sie Logik, um unsichtbare Denkaufgaben zu lösen. Obwohl dieser Ansatz Leistungsverbesserungen mit sich bringt, ist er stark auf umfangreiches Training und zusätzliche Datenaufbereitung angewiesen [8,9].
Der Llama-3-Bericht [10] hebt eine wichtige Beobachtung hervor: Wenn Modelle mit einem anspruchsvollen Inferenzproblem konfrontiert werden, generieren sie manchmal korrekte Inferenztrajektorien. Dies deutet darauf hin, dass das Modell weiß, wie es die richtige Antwort liefert, aber Schwierigkeiten bei der Auswahl hat. Basierend auf dieser Erkenntnis stellten wir eine einfache Frage: Können wir die Argumentationsfähigkeiten von LLMs verbessern, indem wir ihnen bei der Auswahl des richtigen Outputs helfen? Um dies zu untersuchen, haben wir ein Experiment durchgeführt, bei dem verschiedene Belohnungsmodelle für die Auswahl der LLM-Ausgaben zum Einsatz kamen. Experimentelle Ergebnisse zeigen, dass die Auswahl auf Stufenebene herkömmliche CoT-Methoden deutlich übertrifft. Abbildung 2 Algorithmus -Architekturdiagramm von Mindstar Wir führen einen neuen Inferenz -Suchframework ein - Mindstar (M*), indem wir die Inferenzaufgabe als Suchproblem behandeln und die Belohnungen des Prozessüberwachungsmodells nutzen (Prozess -Supervised Reward Model, PRM), M* navigiert effektiv im Inferenzbaumraum und identifiziert annähernd optimale Pfade. Durch die Kombination der Ideen von Beam Search (BS) und Levin Tree Search (LevinTS) wird die Sucheffizienz weiter verbessert und der optimale Argumentationspfad innerhalb begrenzter Rechenkomplexität gefunden. 2.1 Process Supervised Reward Model (Prozessüberwachtes Belohnungsmodell) Dieser Ansatz baut auf dem Erfolg von PRM in anderen Anwendungen auf. Insbesondere verwendet PRM den aktuellen Argumentationspfad und den möglichen nächsten Schritt als Eingabe und gibt einen Belohnungswert
zurück. PRM bewertet neue Schritte, indem es den gesamten aktuellen Denkverlauf berücksichtigt und so Konsistenz und Treue zum Gesamtpfad fördert. Ein hoher Belohnungswert zeigt an, dass der neue Schritt für einen bestimmten Argumentationspfad
wahrscheinlich richtig ist, sodass der Erweiterungspfad eine weitere Erkundung wert ist. Umgekehrt weist ein niedriger Belohnungswert darauf hin, dass der neue Schritt möglicherweise falsch ist, was bedeutet, dass die Lösung, die diesem Pfad folgt, möglicherweise ebenfalls falsch ist. Der 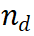
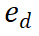
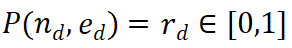 M*-Algorithmus besteht aus zwei Hauptschritten, die iterieren, bis die richtige Lösung gefunden ist: 1. Inferenzpfaderweiterung: In jeder Iteration generiert das zugrunde liegende LLM den nächsten Schritt des aktuellen Inferenzpfads .
M*-Algorithmus besteht aus zwei Hauptschritten, die iterieren, bis die richtige Lösung gefunden ist: 1. Inferenzpfaderweiterung: In jeder Iteration generiert das zugrunde liegende LLM den nächsten Schritt des aktuellen Inferenzpfads . 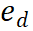
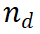 2. Bewertung und Auswahl: Verwenden Sie PRM, um die generierten Schritte zu bewerten und basierend auf diesen Bewertungen den Argumentationspfad für die nächste Iteration auszuwählen. 2.2 InferenzpfaderweiterungNachdem wir den zu erweiternden Inferenzpfad ausgewählt hatten
2. Bewertung und Auswahl: Verwenden Sie PRM, um die generierten Schritte zu bewerten und basierend auf diesen Bewertungen den Argumentationspfad für die nächste Iteration auszuwählen. 2.2 InferenzpfaderweiterungNachdem wir den zu erweiternden Inferenzpfad ausgewählt hatten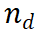 , haben wir eine Eingabeaufforderungsvorlage (Beispiel 3.1) entworfen, um die nächsten Schritte aus dem LLM zu sammeln. Wie das Beispiel zeigt, behandelt LLM die ursprüngliche Frage als {question} und den aktuellen Argumentationspfad als {answer}. Beachten Sie, dass in der ersten Iteration des Algorithmus der ausgewählte Knoten der Wurzelknoten ist, der nur die Frage enthält, sodass {answer} leer ist. Für einen Inferenzpfad
, haben wir eine Eingabeaufforderungsvorlage (Beispiel 3.1) entworfen, um die nächsten Schritte aus dem LLM zu sammeln. Wie das Beispiel zeigt, behandelt LLM die ursprüngliche Frage als {question} und den aktuellen Argumentationspfad als {answer}. Beachten Sie, dass in der ersten Iteration des Algorithmus der ausgewählte Knoten der Wurzelknoten ist, der nur die Frage enthält, sodass {answer} leer ist. Für einen Inferenzpfad  generiert LLM N Zwischenschritte und hängt sie als untergeordnete Elemente des aktuellen Knotens an. Im nächsten Schritt des Algorithmus werden diese neu generierten untergeordneten Knoten ausgewertet und ein neuer Knoten für die weitere Erweiterung ausgewählt. Wir haben auch erkannt, dass eine andere Möglichkeit zum Generieren von Schritten darin besteht, das LLM mithilfe von Schrittmarkierungen zu optimieren. Dies kann jedoch die Inferenzfähigkeit von LLM verringern, und was noch wichtiger ist, es widerspricht dem Ziel dieses Artikels, die Inferenzfähigkeit von LLM zu verbessern, ohne die Gewichte zu ändern. 2.3 Auswahl des Inferenzpfads Nach der Erweiterung des Inferenzbaums verwenden wir ein vorab trainiertes prozedural überwachtes Belohnungsmodell (PRM), um jeden neu generierten Schritt zu bewerten. Wie bereits erwähnt, nimmt PRM einen Pfad und einen Schritt und gibt den entsprechenden Belohnungswert zurück. Nach der Auswertung benötigen wir einen Baumsuchalgorithmus, um den nächsten zu erweiternden Knoten auszuwählen. Unser Framework basiert nicht auf einem bestimmten Suchalgorithmus, und in dieser Arbeit instanziieren wir zwei Suchmethoden, die am besten zuerst sind, nämlich Beam Search und Levin Tree Search. 3. Ergebnisse und Diskussion Eine umfassende Auswertung von GSM8K- und MATH-Datensätzen zeigt, dass M* die Inferenzfähigkeiten von Open-Source-Modellen (wie LLaMA-2) erheblich verbessert und seine Leistung vergleichbar ist Es ist mit größeren Closed-Source-Modellen (wie GPT-3.5 und Grok-1) vergleichbar und reduziert gleichzeitig die Modellgröße und die Rechenkosten erheblich. Diese Ergebnisse unterstreichen das Potenzial der Verlagerung von Rechenressourcen von der Feinabstimmung auf die Inferenzzeitsuche und eröffnen neue Wege für die zukünftige Forschung zu effizienten Techniken zur Inferenzverbesserung.
generiert LLM N Zwischenschritte und hängt sie als untergeordnete Elemente des aktuellen Knotens an. Im nächsten Schritt des Algorithmus werden diese neu generierten untergeordneten Knoten ausgewertet und ein neuer Knoten für die weitere Erweiterung ausgewählt. Wir haben auch erkannt, dass eine andere Möglichkeit zum Generieren von Schritten darin besteht, das LLM mithilfe von Schrittmarkierungen zu optimieren. Dies kann jedoch die Inferenzfähigkeit von LLM verringern, und was noch wichtiger ist, es widerspricht dem Ziel dieses Artikels, die Inferenzfähigkeit von LLM zu verbessern, ohne die Gewichte zu ändern. 2.3 Auswahl des Inferenzpfads Nach der Erweiterung des Inferenzbaums verwenden wir ein vorab trainiertes prozedural überwachtes Belohnungsmodell (PRM), um jeden neu generierten Schritt zu bewerten. Wie bereits erwähnt, nimmt PRM einen Pfad und einen Schritt und gibt den entsprechenden Belohnungswert zurück. Nach der Auswertung benötigen wir einen Baumsuchalgorithmus, um den nächsten zu erweiternden Knoten auszuwählen. Unser Framework basiert nicht auf einem bestimmten Suchalgorithmus, und in dieser Arbeit instanziieren wir zwei Suchmethoden, die am besten zuerst sind, nämlich Beam Search und Levin Tree Search. 3. Ergebnisse und Diskussion Eine umfassende Auswertung von GSM8K- und MATH-Datensätzen zeigt, dass M* die Inferenzfähigkeiten von Open-Source-Modellen (wie LLaMA-2) erheblich verbessert und seine Leistung vergleichbar ist Es ist mit größeren Closed-Source-Modellen (wie GPT-3.5 und Grok-1) vergleichbar und reduziert gleichzeitig die Modellgröße und die Rechenkosten erheblich. Diese Ergebnisse unterstreichen das Potenzial der Verlagerung von Rechenressourcen von der Feinabstimmung auf die Inferenzzeitsuche und eröffnen neue Wege für die zukünftige Forschung zu effizienten Techniken zur Inferenzverbesserung. 
Tabelle 1 zeigt die Vergleichsergebnisse verschiedener Schemata für die GSM8K- und MATH-Inferenzbenchmarks. Die Zahl für jeden Eintrag gibt den Prozentsatz des gelösten Problems an. Die Notation SC@32 stellt die Selbstkonsistenz zwischen 32 Kandidatenergebnissen dar, während n-Shot die Ergebnisse von Beispielen mit wenigen Schüssen darstellt. CoT-SC@16 bezieht sich auf die Selbstkonsistenz zwischen 16 Chain of Thought (CoT)-Kandidatenergebnissen. BS@16 stellt die Strahlsuchmethode dar, die 16 Kandidatenergebnisse auf jeder Schrittebene umfasst, während LevinTS@16 die Levin-Baum-Suchmethode unter Verwendung der gleichen Anzahl von Kandidatenergebnissen detailliert beschreibt. Es ist erwähnenswert, dass das neueste Ergebnis für GPT-4 im MATH-Datensatz GPT-4-turbo-0409 ist, was wir besonders hervorheben, da es die beste Leistung in der GPT-4-Familie darstellt. 
Abbildung 3 Wir untersuchen, wie sich die M*-Leistung ändert, wenn sich die Anzahl der Kandidaten auf Stufenebene ändert. Wir haben Llama-2-13B als Basismodell und Beam Search (BS) als Suchalgorithmus ausgewählt. 
Abbildung 4 Skalierungsgesetze der Modellfamilien Llama-2 und Llama-3 im MATH-Datensatz. Alle Ergebnisse stammen aus ihren Originalquellen. Wir verwenden Scipy-Tools und logarithmische Funktionen, um die angepassten Kurven zu berechnen. 
Tabelle 2 Durchschnittliche Anzahl von Token, die durch verschiedene Methoden bei der Beantwortung von Fragen erzeugt werdenIn diesem Artikel wird MindStar (M*) vorgestellt, ein neuartiges suchbasiertes Argumentationsframework zur Verbesserung der Inferenzfähigkeiten von vorab trainierten großen Sprachmodellen. Indem M* die Inferenzaufgabe als Suchproblem behandelt und ein Belohnungsmodell der Prozessüberwachung nutzt, navigiert M* effizient im Inferenzbaumraum und identifiziert nahezu optimale Pfade. Durch die Kombination der Ideen der Strahlsuche und der Levin-Tree-Suche wird die Sucheffizienz weiter verbessert und sichergestellt, dass der beste Argumentationspfad innerhalb einer begrenzten Rechenkomplexität gefunden werden kann. Umfangreiche experimentelle Ergebnisse zeigen, dass M* die Inferenzfähigkeiten von Open-Source-Modellen erheblich verbessert und seine Leistung mit größeren Closed-Source-Modellen vergleichbar ist, während gleichzeitig die Modellgröße und die Rechenkosten deutlich reduziert werden. Diese Forschungsergebnisse zeigen, dass die Verlagerung von Rechenressourcen von der Feinabstimmung auf die Inferenzzeitsuche ein großes Potenzial birgt und neue Wege für die zukünftige Forschung zu effizienten Inferenzverbesserungstechnologien eröffnet. [1] Nisan Stiennon, Long Ouyang, Jeffrey Wu, Daniel Ziegler, Ryan Lowe, Chelsea Voss, Alec Radford, Dario Amodei und Paul F. Christiano mit menschlichem Feedback. Advances in Neural Information Processing Systems, 33:3008–3021, 2020.[2] Long Ouyang, Jeffrey Wu, Agarwal, Katarina Slama, Alex Ray, et al. Training von Sprachmodellen zur Befolgung von Anweisungen mit menschlichem Feedback, Fortschritte in neuronalen Informationsverarbeitungssystemen, 35:27730–27744, 2022. [3] Ziyang Luo, Can Xu , Pu Zhao, Qingfeng Sun, Xiubo Geng, Wenxiang Hu, Chongyang Tao, Jing Ma, Qingwei Lin und Daxin Jiang [4] Mark Chen, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde de Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, et al. Evaluierung großer Sprachmodelle, die auf arXiv trainiert wurden Vorabdruck arXiv:2107.03374, 2021.[5] Eine Konföderation von Modellen: Eine umfassende Bewertung von Filmen zum Thema kreatives Schreiben [6] Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T Kwok, Zhenguo Li, Adrian Weller und Weiyang Liu. Bootstrap Ihre eigenen mathematischen Fragen für große arXiv Preprint arXiv:2309.12284, 2023. [7] Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Mingchuan Zhang, YK Li, Y Wu und Daya Guo. Deepseekmath: Die Grenzen überschreiten Mathematische Argumentation in offenen Sprachmodellen. arXiv-Preprint arXiv:2402.03300, 2024 . arXiv-Vorabdruck arXiv:2310.06786, 2023.[9] Peiyi Wang, Lei Li, Zhihong Shao, RX Xu, Damai Dai, Yifei Li, Deli Chen, Y Wu und Zhifang Sui: Verifizieren und verstärken Sie LMs Schritt für Schritt ohne menschliche Anmerkungen. URL https://ai.meta.com/blog/meta-llama-3/. Zugriff: 2024-04-30.Das obige ist der detaillierte Inhalt vonIch kann es kaum erwarten, dass OpenAIs Q*, Huawei Noahs Geheimwaffe MindStar zur Erforschung von LLM-Argumentation, als Erstes hier ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Stellungnahme:Der Inhalt dieses Artikels wird freiwillig von Internetnutzern beigesteuert und das Urheberrecht liegt beim ursprünglichen Autor. Diese Website übernimmt keine entsprechende rechtliche Verantwortung. Wenn Sie Inhalte finden, bei denen der Verdacht eines Plagiats oder einer Rechtsverletzung besteht, wenden Sie sich bitte an admin@php.cn



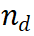
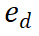
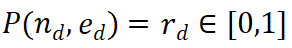 M*-Algorithmus besteht aus zwei Hauptschritten, die iterieren, bis die richtige Lösung gefunden ist:
M*-Algorithmus besteht aus zwei Hauptschritten, die iterieren, bis die richtige Lösung gefunden ist: 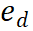
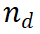 2. Bewertung und Auswahl: Verwenden Sie PRM, um die generierten Schritte zu bewerten und basierend auf diesen Bewertungen den Argumentationspfad für die nächste Iteration auszuwählen.
2. Bewertung und Auswahl: Verwenden Sie PRM, um die generierten Schritte zu bewerten und basierend auf diesen Bewertungen den Argumentationspfad für die nächste Iteration auszuwählen. 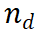 , haben wir eine Eingabeaufforderungsvorlage (Beispiel 3.1) entworfen, um die nächsten Schritte aus dem LLM zu sammeln. Wie das Beispiel zeigt, behandelt LLM die ursprüngliche Frage als {question} und den aktuellen Argumentationspfad als {answer}. Beachten Sie, dass in der ersten Iteration des Algorithmus der ausgewählte Knoten der Wurzelknoten ist, der nur die Frage enthält, sodass {answer} leer ist. Für einen Inferenzpfad
, haben wir eine Eingabeaufforderungsvorlage (Beispiel 3.1) entworfen, um die nächsten Schritte aus dem LLM zu sammeln. Wie das Beispiel zeigt, behandelt LLM die ursprüngliche Frage als {question} und den aktuellen Argumentationspfad als {answer}. Beachten Sie, dass in der ersten Iteration des Algorithmus der ausgewählte Knoten der Wurzelknoten ist, der nur die Frage enthält, sodass {answer} leer ist. Für einen Inferenzpfad  generiert LLM N Zwischenschritte und hängt sie als untergeordnete Elemente des aktuellen Knotens an. Im nächsten Schritt des Algorithmus werden diese neu generierten untergeordneten Knoten ausgewertet und ein neuer Knoten für die weitere Erweiterung ausgewählt. Wir haben auch erkannt, dass eine andere Möglichkeit zum Generieren von Schritten darin besteht, das LLM mithilfe von Schrittmarkierungen zu optimieren. Dies kann jedoch die Inferenzfähigkeit von LLM verringern, und was noch wichtiger ist, es widerspricht dem Ziel dieses Artikels, die Inferenzfähigkeit von LLM zu verbessern, ohne die Gewichte zu ändern.
generiert LLM N Zwischenschritte und hängt sie als untergeordnete Elemente des aktuellen Knotens an. Im nächsten Schritt des Algorithmus werden diese neu generierten untergeordneten Knoten ausgewertet und ein neuer Knoten für die weitere Erweiterung ausgewählt. Wir haben auch erkannt, dass eine andere Möglichkeit zum Generieren von Schritten darin besteht, das LLM mithilfe von Schrittmarkierungen zu optimieren. Dies kann jedoch die Inferenzfähigkeit von LLM verringern, und was noch wichtiger ist, es widerspricht dem Ziel dieses Artikels, die Inferenzfähigkeit von LLM zu verbessern, ohne die Gewichte zu ändern. 




