javascript - HTML5中如何判断某坐标位于多边形区域内（签到功能）？求帮忙！！！！

Question

想要通过HTML5和NodeJs来做个地理定位和LBS签到功能，因为web端地理围栏相关的技术文档似乎没有，百度和高德的api也没用提供地理围栏的功能，想要另辟蹊径来完成这个功能。 因此考虑到，能不能通过百度API或高德A...

PHP中文网 · Answer

这个东西实际上还有点复杂，之前刚好搞过地图引擎，可以说说。对于问题 如何判断坐标位于多边形区域内中间涉及到几个部分:

1) 如果是一个标准平面坐标体系，这是一个标准的PIP(Point in Polygon)的问题，已经有不少算法来实现。详细的资料在http://geomalgorithms.com/a03-_inclusion.html, http://alienryderflex.com/polygon/和wiki 以及stackoverflow有描述。

其中射线法的基本思路是画一条以点为起点垂直y轴的射线，判断和多边形边的交点个数，如果是奇数就是在多边形内，如果是偶数就是在多边形外。

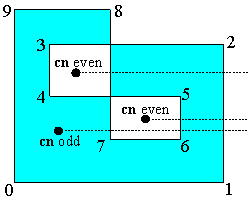
然后是卷绕数(winding number)法，看以点为中心，考虑多边形的边作为一个顺时针曲线绕这个点的次数，如果绕过0圈就是在多边形外，否则就是在多边形内。

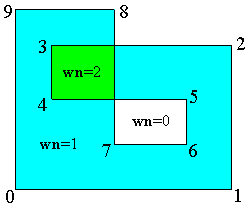
可以看到winding number更加准确些，有些资料说winding number计算量大，实际上新的算法只要计算绕圈个数而不用涉及反三角函数。

自己之前实现的一个基于winding number的，因为要判断复杂多边形，如果只是简单多边形, ray casting也就可以了。

其中参数(x, y)是坐标点, coords是[x1, y1, x2, y2, x3, y3,...., x1, y1]这样的多边形边坐标，记得要闭合形成闭合曲线

/** 
 * PIP problem, Winding number
 * @param {number} x
 * @param {number} y
 * @param {Array.} coords
 */
function isPointInPolygon(x, y, coords) {
    var wn = 0;
    for (var shiftP, shift = coords[1] > y, i = 3; i < coords.length; i += 2) {
        shiftP = shift;
        shift = coords[i] > y;
        if (shiftP != shift) {
            var n = (shiftP ? 1 : 0) - (shift ? 1 : 0);
            // dot product for vectors (c[0]-x, c[1]-y) . (c[2]-x, c[3]-y)
            if (n * ((coords[i - 3] - x) * (coords[i - 0] - y) - (coords[i - 2] - y) * (coords[i - 1] - x)) > 0)
                wn += n;
        }
    }
    return wn;
}

2) 因为你碰到的问题是一个地理坐标，这使得问题变得复杂了，因为地理坐标并不是标准平面，不能把经纬度坐标放进去算。而是一个近球面体系（一般按照球体来做计算差别不会很大，虽然地球是椭圆的），而且有太多不同的坐标系，当时头都大了。不过目前通用的就是墨卡托坐标系，高德google腾讯地图都是这样，百度有自己的BD09，实际也是墨卡托的变种，加上了自己的一些转换。不过地图的api都提供经纬度转换像素点的功能，可以找找看LatLng转换到Point的api。或者自己实现一个墨卡托投影转化也是可以的。

转化完之后就可以使用第一步中的算法判断点是否坐标点是否在转化完之后形成的多边形内了。

3）其实没有什么3了，只不过墨卡托投影在处理南北极上有很大形变，比如包含南极的点是在无穷远处，而且一个在南北极点的多变性在投影下已经不是多边形了，有兴趣可以自己去看下。这种情况下只能去找黎曼几何中的球面几何上类似的算法了... 我看着已经要疯了。不过好在南北极都不怎么住人，用的人很少，经纬度的设定真是很贴心呢。

javascript - HTML5中如何判断某坐标位于多边形区域内（签到功能）？求帮忙！！！！

全部回复(1)我来回复