AI颠覆数学研究！菲尔兹奖得主、华裔数学家领衔11篇顶刊论文｜陶哲轩转赞
- WBOY转载
- 2024-04-09 11:52:07722浏览
AI，的确正在改变数学。
最近，一直十分关注这个议题的陶哲轩，转发了最近一期的《美国数学学会通报》（Bulletin of the American Mathematical Society）。
围绕「机器会改变数学吗？」这个话题，众多数学家发表了自己的观点，全程火花四射，内容硬核，精彩纷呈。
作者阵容强大，包括菲尔兹奖得主Akshay Venkatesh、华裔数学家郑乐隽、纽大计算机科学家Ernest Davis等多位业界知名学者。
AI的世界已经发生了天翻地覆的变化，要知道，其中很多文章是在一年前提交的，而在这一年内，AI已经有了很多显着的变化。
然而，尽管如此，这些文章依旧含金量满满，甚至让陶哲轩高呼：这个领域太快了！让我还没发表的文章显得有些多余。
无人可以否认，如今AI工具正在让数学领域以惊人的速度向前迈进。
人工智能是否将引领包括纯数学在内的科学领域，在信息收集和处理方式上的一场革命？它会改变数学研究方法吗？
对此，数学家们的意见产生了分歧：某些人认为，机器学习在研究中的广泛应用即将到来，而另一些人则持怀疑态度，他们回顾了1960年代的过度乐观和随后的「AI寒冬」。
然而，数学研究实践中，已经极有可能发生剧变。现在，数学家们是时候考虑这些变化所带来的问题了。
不用怀疑，风暴就在前方。
那么，机器会改变数学吗？
数学自动化对数学研究的影响
在这篇论文中，菲尔兹奖得主Akshay Venkatesh探讨了自动化对数学研究的影响。
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024- 01834-5/S0273-0979-2024-01834-5.pdf
在这篇论文中，Akshay Venkatesh提出了一个有趣的思想实验——
2017年，DeepMind的Alphazero一夜之间自学了国际象棋和围棋，超越了人类。
如果十年后，「Alephzero」（写作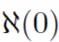
），也做了同样的格式化数学呢？
本文中的「数学」指的是「纯数学研究」。
我们的出发点是假设「Alephzero」自学了高中和大学数学，并做完了SpringerVerlag Graduate Terts in Mathematics 系列的所有习题。第二天早上，数学家们将它放出，下载它的孩子们，用我们的计算资源运行它们。
这的确是一个思想实验，因为它显然是不现实的：通过把我们的视野限制在未来的十年或二十年，我们允许自己脱离可能伴随这种技术进步而发生的社会变革来考虑这个问题，也允许我们避免思考更极端的机器智能类型，我们把「Alephzero」当作一个电动工具而不是一个有生命的合作者来建模。
我们可以这样安慰自己：实际上，这个前提离我们太遥远了，我们不需要考虑它。但是，如果我们允许哪怕是微乎其微的可能性，这种情况可能会在二十年后发生。
通过数学家和问题网络中的贝叶斯相互作用，提供了一个非常粗略的模型，展示了我们的部分价值机制。我们现在考虑「Alephzero」将如何影响这个网络并改变结果。
正如我们所看到的，感知到的困难是我们构建价值的重要组成部分。
无论具体情况如何，「Alephzero」都会改变我们解决问题的能力，从而改变我们对问题难度的看法。
数学过程中可以加速最快的部分将在其感知难度上降低最大，并且根据我们上面的模型，状态将遭受最大的降低。类似的模式发生在许多自动化实例中。
最后，「Alephzero」将大大扩展数学上有趣问题的整个范围。它会在专业数学家和其他人之间，创造公平的竞争环境。
机器怎样让数学更聚合
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01827-8/S0273-0979-2024-01827-8.pdf
数学家郑乐隽认为，既然技术已经改变了我们研究数学的方式，那就可以利用这项技术让数学更具「聚合」，而不是让人类数学家在面对技术进步时变得多余。
在思考「研究数学」意味着什么时，她研究了数学技术的以下几个方面：教学和学习、提出问题、协作、传播和做研究的行为。
这并不是一个严谨的分析，而是基于她作为数学家经验的明智反思。
郑乐隽认为，虽然现在有一些计算机辅助的校对检查器，甚至证明生成器，但技术还没有真正侵占数学研究最深刻、最有创意、最人性化的方面。
深层的创造性部分首先涉及提出想法——定义的想法、证明的想法、在数学的不同部分之间建立联系的想法、表达事物的新方法的想法、符号和术语的想法、图解推理的想法以及视觉表示的想法。
为了让机器做数学研究，我们必须想办法告诉它们去做，如果我们自己还不知道怎么做，那么我们就很难告诉它们怎么做。
机器可以进行一定程度的证明检查，但暗地里，数学家们都知道，我们写不出完全严格的证明——我们根据逻辑提出论点，并由我们认为同行能够填写的逻辑步骤来支持。
我们没有定义这些步骤的大小，所以很难告诉机器去做。
生成证明是一种完全不同的技能，而不仅仅是检查它们，任何数学学生都知道。能够遵循别人的证据，比自己想出一个新的证据要容易得多。这并不是说计算机在数学研究能力上永远不可能超过人类数学家。
在她看来，计算机比人类数学家更厉害的地方就在于——
它们有更大的能力来搜索所有可能的动作，通过搜索目前已知的所有可能的逻辑结果，它们就能尝试提出新的数学。
这需要想象力、猜测和直觉的飞跃，什么足以让计算机做到这一点？这个想法非常有趣。
计算机能帮我们做逻辑推理吗
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01833-3/S0273-0979-2024-01833-3.pdf
计算机已经彻底变革了我们进行数学研究的方法，让复杂的计算变得轻而易举。
但接下来，它们是否会成为我们逻辑推理的助手？甚至有朝一日，它们能否独立进行推理呢？
本文将带你一览神经网络、计算机定理证明器以及大语言模型在近期的重要进展。
形式化工具如何帮我们更好地做数学研究
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01832-1/S0273-0979-2024-01832-1.pdf
从20世纪初开始，我们就明白，数学定义和证明能够通过拥有严格语法和规则的形式系统得到表示。
在这一基础上，计算机证明助手的发展让我们能够将数学知识以数字化的形式进行编码。
本文将探讨这类技术及其相关工具如何帮助我们更好地进行数学研究。
用定理证明器，简化数学研究中的复杂问题
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01831-X/S0273-0979-2024-01831-X.pdf
本文探讨了如何利用交互式定理证明器通过设定抽象边界来简化数学研究中的复杂问题。
奇异的新宇宙：LLM让数学家用更自然的语言和证明助手交流
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01830-8/S0273-0979-2024-01830-8.pdf
目前的计算机程序，也就是证明助手，能够校验数学证明的正确性，但它们使用的专业证明语言对很多数学家而言构成了一道门槛。
大语言模型（LLM）具有打破这一障碍的可能性，让数学家们能够用更自然的语言与证明助手进行交流。这样不仅能够培养他们的直觉，还能确保他们的论证过程正确无误。
用深度学习工具做纯数学研究
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01829-1/S0273-0979-2024-01829-1.pdf
本文是关于一位纯数学家在研究中尝试使用深度学习工具时，可能会期待的个人体验和非正式分享。
AI能做数学研究吗
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01828-X/S0273-0979-2024-01828-X.pdf
本文探讨了目前AI技术在解决融合了基础数学和常识推理的文字题目方面的能力和局限。
作者回顾了三种利用AI自然语言技术开发的方法：直接给出答案、生成解题的计算机程序，以及生成可供自动定理验证器使用的形式化表述。
作者认为，这些限制在发展纯数学研究用的AI技术中的重要性尚未明确，但它们在数学应用中极为关键，并且在开发能够理解人类编写的数学内容的程序时也很重要。
机器时代下的证明是怎样的
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01826-6/S0273-0979-2024-01826-6.pdf
作者在本文中探讨了证明的本质及其在机器时代的演变，并通过对比传统验证和计算机验证中的价值观进行了分析。
文章最终提出的方法可能使计算机证明借鉴人类经验中的成功策略。
自动化，让数学家反思自己的价值
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01825-4/S0273-0979-2024-01825-4.pdf
在这篇论文中，作者严厉地批评了同行们缺乏思考，尤其是在考虑数学的机械化未来时，他们忽视了社会更广泛层面上关于技术和人工智能的重要辩论。
p-adic数域中的连分数
论文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01819-9/S0273-0979-2024-01819-9.pdf
连分数在数论特别是丢番图逼近这一领域享有悠久的历史。
本文旨在概述p-adic连分数理论的核心成果，这是一种定义在p-adic数域Qp上的连分数。
内容将从基本概念讲起，直至介绍最新进展和当前面临的开放性问题。
陶哲轩发文：机器辅助证明
顺便，陶哲轩也安利了一下自己之前写的论文「Machine assisted proof」。
论文地址：https://terrytao.files.wordpress.com/2024/03/machine-assisted-proof-notices.pdf
在这篇论文中陶哲轩表示，借助于LLM处理自然语言输入的能力，它们很可能成为一个用户友好的平台，使得那些不具备特定软件知识的数学家也能够使用高级工具。
如今，他和很多科学家已经习惯使用这些模型来生成各种语言的简单代码，包括符号代数包，或者制作复杂的图表和图像了。
目前，由于形式化证明验证（formal proof verification）工作非常依赖人力，这使得实时将大量当前研究论文完全形式化变得不切实际。
在偏微分方程领域中，常常需要通过多页的计算来估计涉及一个或多个未知函数（比如PDE的解）的积分表达式。
其中便涉及到使用这些函数在不同函数空间范数（如Sobolev空间范数）中的界限，结合标准不等式（例如Hölder不等式和Sobolev不等式），以及诸如分部积分或积分符号下的微分等恒等式。
这类计算虽然是常规操作，但可能包含各种程度的错误（如符号错误），对审稿人来说，细致地检查这些计算既枯燥又费时，而且这些计算本身除了最终的估计结果是正确的之外，很难提供更深入的数学理解或见解。
可以设想，未来可能开发出工具，以自动或半自动的方式建立数学估计，并且将目前那些既冗长又缺乏启发性的估计证明替换为一个指向形式证明证书的链接。
更进一步，我们也许能够期待，基于一组初始的假设和方法，未来的AI工具能够提出它所能得出的最佳估计，而无需先进行纸笔计算来预测这个估计可能是什么。
目前来看，估计可能的状态空间过于复杂，难以自动化地进行探索；但随着技术的发展，实现这种自动化探索的可能性并非遥不可及。
一旦实现，我们就能在目前看来不可行的规模上进行数学探索。
还是以偏微分方程为例，目前的研究通常一次只研究一到两个方程；但在未来，我们可能能同时研究数百个方程。
例如，先对一个方程完整地展开论证，然后让AI工具将这些论证调整适用于大量相关的方程族，必要时，当论证的扩展出现非常规情况时，AI会向作者提问。
如今，在数学的其他领域，比如图论，这种大规模数学探索的初步迹象已经开始显现。
但目前的这些初步尝试，由于依赖于计算量极大的AI模型或需要大量的专家级人工参与和监督，因此难以大规模推广。
然而，陶哲轩相信在不远的将来，我们将见证更多创新的机器辅助数学方法的诞生。
以上是AI颠覆数学研究！菲尔兹奖得主、华裔数学家领衔11篇顶刊论文｜陶哲轩转赞的详细内容。更多信息请关注PHP中文网其他相关文章！