机率密度函数的简单说明
机率密度函数(p.d.f.,probability density function)描述了随机变量的概率分布,为累积分布函数的导函数。 [编辑]定义 对于一维实随机变量X,任何一个满足下列条件的函数都可以被定义为其概率密度函数:
一束粒子被一个障碍物﹝位於x = 0﹞给分散,其波函数为下:
Ψ(x, t) = Ae-iEt/h[当 x
Ψ(x, t) = e-iEt/h( Beikx+ Ce-ikx) [当 x> 0 ]
其中 E = h2k2/( 2m ) 及 k > 0,A、B及C为复杂系数 (complex coefficient)。
﹝其中的「h」为「h-bar」,就是h上面一横﹞
(a) 算出其机率密度 p(x, t)当x
(b) 算出其机率流密度 j(x, t)当x
(c) 算出其机率密度 p(x, t)当x > 0。
(d) 算出其机率流密度 j(x, t)当x > 0。
(e) 上面的波函数含三个不同的部份,A、B及C三个系数,说出每一个是右移还是左移。它们三个分别代表入射、反射及发射,那个是那个?
注:p(x, t)及j(x, t)的答案必定是实数。
概率函数与概率密度怎么区分
概率密度的数学定义
对于随机变量X,若存在一个非负可积函数p(x)(﹣∞
连续型随机变量往往通过其概率密度函数进行直观地描述,连续型随机变量的概率密度函数f(x)具有如下性质:
这里指的是一维连续随机变量,多维连续变量也类似。
随机数据的概率密度函数:表示瞬时幅值落在某指定范围内的概率,因此是幅值的函数。它随所取范围的幅值而变化。
密度函数f(x) 具有下列性质:
(1)f(x)≧0;
(2) ∫f(x)d(x)=1;
(3) P(a 解题过程如下: 扩展资料 概率密度的方法: 设随机变量X具有概率密度fX(x),-∞ 单纯的讲概率密度没有实际的意义,它必须有确定的有界区间为前提。可以把概率密度看成是纵坐标,区间看成是横坐标,概率密度对区间的积分就是面积,而这个面积就是事件在这个区间发生的概率,所有面积的和为1。所以单独分析一个点的概率密度是没有任何意义的,它必须要有区间作为参考和对比。 概率指事件随机发生的机率,对于均匀分布函数,概率密度等于一段区间(事件的取值范围)的概率除以该段区间的长度,它的值是非负的,可以很大也可以很小。 从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率为m/n。经过大量反复试验,常有m/n越来越接近于某个确定的常数(此论断证明详见伯努利大数定律)。
设随机变量X N0 1 Y |x| Y的概率密度函数

以上是机率密度函数的简单说明的详细内容。更多信息请关注PHP中文网其他相关文章!
 在启动时接收NVVSVC.EXE运行时错误?在这里看!Apr 11, 2025 am 12:50 AM
在启动时接收NVVSVC.EXE运行时错误?在这里看!Apr 11, 2025 am 12:50 AM您在启动时会遇到NVVSVC.EXE运行时错误吗?更糟糕的是,你们中的一些人可能最终会出现黑屏。因此,您迫切需要尽快删除此错误。在PHP.CN网站上的本指南中,我们收集了一些可行的SOL
 Windows P的高级提示不适用于WindowsApr 11, 2025 am 12:49 AM
Windows P的高级提示不适用于WindowsApr 11, 2025 am 12:49 AM如果您有多个显示器,则必须熟悉Windows P快捷方式。但是,窗口P无法正常工作,可能会偶尔发生。如果您面临此问题,则PHP.CN的这篇文章确实可以为您提供帮助。
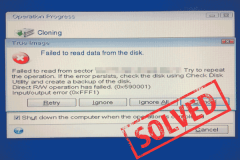 如果Acronis克隆未能从磁盘中读取数据怎么办?Apr 11, 2025 am 12:48 AM
如果Acronis克隆未能从磁盘中读取数据怎么办?Apr 11, 2025 am 12:48 AMAcronis克隆的问题未能从磁盘中读取数据,通常会在克隆过程中出现。面对这个无聊的问题,您该怎么办?尝试修复它。或者,您可以运行Acronis True Image的替代方案 - php.cn软件
 文件上传未实现 - 以下是4种方法!Apr 11, 2025 am 12:47 AM
文件上传未实现 - 以下是4种方法!Apr 11, 2025 am 12:47 AM当您尝试从文件夹访问Word文档时,您可能会收到一个错误,该错误在单击它后才说“未实现”。来自PHP.CN的这篇文章介绍了如何修复“未实现的文件上传”问题。
 Windows中的AI:Windows中的AI驱动功能Apr 11, 2025 am 12:46 AM
Windows中的AI:Windows中的AI驱动功能Apr 11, 2025 am 12:46 AM微软已经在AI上投入了大量的人力和财政资源,并取得了出色的成果。在这篇文章中,PHP.CN将在Windows中谈论AI,包括Windows 11和Windows 10中的AI工具和功能。
 如何使用Windows 10 0x80070643错误的PowerShell脚本错误?Apr 11, 2025 am 12:45 AM
如何使用Windows 10 0x80070643错误的PowerShell脚本错误?Apr 11, 2025 am 12:45 AMKB5034441无法使用错误代码0x80070643安装?来自Microsoft的Windows 10 0x80070643的PowerShell脚本有助于自动化更新Winre分区以修复Bitlocker安全功能旁路漏洞。 php.cn向你指导你
 在哪里可以找到矛盾:操作galuga在PC上保存文件位置Apr 11, 2025 am 12:44 AM
在哪里可以找到矛盾:操作galuga在PC上保存文件位置Apr 11, 2025 am 12:44 AMContra:Galuga行动是由Konami出版的新发行的射手视频游戏。在这里,PHP.CN软件上的这篇文章重点关注Contra:操作Galuga保存文件位置,并说明如何备份Contra:操作Galuga保存文件。
 无法在Microsoft Word中突出显示文字吗?在这里经过验证的方式Apr 11, 2025 am 12:43 AM
无法在Microsoft Word中突出显示文字吗?在这里经过验证的方式Apr 11, 2025 am 12:43 AMMicrosoft Word为我们所有人提供了许多有用的功能,包括突出显示文本。但是,有些人最近遇到了一个问题,即他们无法用Microsoft Word强调文本。这个问题给他们带来了不便。如果你是其中之一


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

WebStorm Mac版
好用的JavaScript开发工具

螳螂BT
Mantis是一个易于部署的基于Web的缺陷跟踪工具,用于帮助产品缺陷跟踪。它需要PHP、MySQL和一个Web服务器。请查看我们的演示和托管服务。

SecLists
SecLists是最终安全测试人员的伙伴。它是一个包含各种类型列表的集合,这些列表在安全评估过程中经常使用,都在一个地方。SecLists通过方便地提供安全测试人员可能需要的所有列表,帮助提高安全测试的效率和生产力。列表类型包括用户名、密码、URL、模糊测试有效载荷、敏感数据模式、Web shell等等。测试人员只需将此存储库拉到新的测试机上,他就可以访问到所需的每种类型的列表。

VSCode Windows 64位 下载
微软推出的免费、功能强大的一款IDE编辑器

Atom编辑器mac版下载
最流行的的开源编辑器





