
孪生神经网络是一种双支路结构的神经网络,常用于相似度度量、分类和检索任务。这种网络的两个支路具有相同的结构和参数。输入分别经过两个支路后,通过相似度度量层(如欧式距离、曼哈顿距离等)进行相似度计算。在训练过程中,通常使用对比损失函数或三元组损失函数。
对比损失函数是针对孪生神经网络的二元分类损失函数,旨在最大限度地将同类样本的相似度调整为接近1,将不同类样本的相似度调整为接近0。其数学表达式如下:
L_{con}(y,d)=ycdot d^2+(1-y)cdotmax(m-d,0)^2
该损失函数用来衡量两个样本之间的相似度,并根据样本的类别进行优化。其中,y表示样本是否属于同一类别,d表示两个样本的相似度,m表示一个预设的边界值。 当y=1时,损失函数的目标是使得d尽可能小,即使两个同类别的样本更加相似。此时,损失函数的值可以通过d的平方来表示,即损失函数的值为d^2。 当y=0时,损失函数的目标是使得d大于m,即使两个不同类别的样本尽可能地不相似。此时,当d小于m时,损失函数的值为d^2,表示样本之间的相似度;当d大于m时,损失函数的值为0,表示样本之间的相似度已经超过了预设的边界值m,不再计算损失
三元组损失函数是一种用于孪生神经网络的损失函数,旨在通过最小化同类样本之间的距离,并最大化不同类样本之间的距离。这种函数的数学表达式如下:
L_{tri}(a,p,n)=max(|f(a)-f(p)|^2-|f(a)-f(n)|^2+margin,0)
其中,a表示锚点样本,p表示同类样本,n表示不同类样本,f表示孪生神经网络的特征提取层,|cdot|表示欧式距离,margin表示一个预设的边界值。损失函数的目标是使得同类样本的距离尽可能小,不同类样本的距离尽可能大,并且大于margin。当同类样本的距离小于不同类样本的距离减去margin时,损失函数的值为0;当同类样本的距离大于不同类样本的距离减去margin时,损失函数的值为两个距离的差值。
对比损失函数和三元组损失函数都是常用的孪生神经网络损失函数,其目标是使得相同类别的样本在特征空间中尽可能靠近,不同类别的样本在特征空间中尽可能远离。在实际应用中,可以根据具体任务和数据集的情况选择合适的损失函数,并结合其他技术(如数据增强、正则化等)进行模型优化。
以上是常见的损失函数在孪生神经网络中的应用的详细内容。更多信息请关注PHP中文网其他相关文章!
 解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM
解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM二元神经网络(BinaryNeuralNetworks,BNN)是一种神经网络,其神经元仅具有两个状态,即0或1。相对于传统的浮点数神经网络,BNN具有许多优点。首先,BNN可以利用二进制算术和逻辑运算,加快训练和推理速度。其次,BNN减少了内存和计算资源的需求,因为二进制数相对于浮点数来说需要更少的位数来表示。此外,BNN还具有提高模型的安全性和隐私性的潜力。由于BNN的权重和激活值仅为0或1,其模型参数更难以被攻击者分析和逆向工程。因此,BNN在一些对数据隐私和模型安全性有较高要求的应用中具
 探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM
探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM在时间序列数据中,观察之间存在依赖关系,因此它们不是相互独立的。然而,传统的神经网络将每个观察看作是独立的,这限制了模型对时间序列数据的建模能力。为了解决这个问题,循环神经网络(RNN)被引入,它引入了记忆的概念,通过在网络中建立数据点之间的依赖关系来捕捉时间序列数据的动态特性。通过循环连接,RNN可以将之前的信息传递到当前观察中,从而更好地预测未来的值。这使得RNN成为处理时间序列数据任务的强大工具。但是RNN是如何实现这种记忆的呢?RNN通过神经网络中的反馈回路实现记忆,这是RNN与传统神经
 计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PM
计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PMFLOPS是计算机性能评估的标准之一,用来衡量每秒的浮点运算次数。在神经网络中,FLOPS常用于评估模型的计算复杂度和计算资源的利用率。它是一个重要的指标,用来衡量计算机的计算能力和效率。神经网络是一种复杂的模型,由多层神经元组成,用于进行数据分类、回归和聚类等任务。训练和推断神经网络需要进行大量的矩阵乘法、卷积等计算操作,因此计算复杂度非常高。FLOPS(FloatingPointOperationsperSecond)可以用来衡量神经网络的计算复杂度,从而评估模型的计算资源使用效率。FLOP
 模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM
模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM模糊神经网络是一种将模糊逻辑和神经网络结合的混合模型,用于解决传统神经网络难以处理的模糊或不确定性问题。它的设计受到人类认知中模糊性和不确定性的启发,因此被广泛应用于控制系统、模式识别、数据挖掘等领域。模糊神经网络的基本架构由模糊子系统和神经子系统组成。模糊子系统利用模糊逻辑对输入数据进行处理,将其转化为模糊集合,以表达输入数据的模糊性和不确定性。神经子系统则利用神经网络对模糊集合进行处理,用于分类、回归或聚类等任务。模糊子系统和神经子系统之间的相互作用使得模糊神经网络具备更强大的处理能力,能够
 改进的RMSprop算法Jan 22, 2024 pm 05:18 PM
改进的RMSprop算法Jan 22, 2024 pm 05:18 PMRMSprop是一种广泛使用的优化器,用于更新神经网络的权重。它是由GeoffreyHinton等人在2012年提出的,并且是Adam优化器的前身。RMSprop优化器的出现主要是为了解决SGD梯度下降算法中遇到的一些问题,例如梯度消失和梯度爆炸。通过使用RMSprop优化器,可以有效地调整学习速率,并且自适应地更新权重,从而提高深度学习模型的训练效果。RMSprop优化器的核心思想是对梯度进行加权平均,以使不同时间步的梯度对权重的更新产生不同的影响。具体而言,RMSprop会计算每个参数的平方
 浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM
浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM深度学习在计算机视觉领域取得了巨大成功,其中一项重要进展是使用深度卷积神经网络(CNN)进行图像分类。然而,深度CNN通常需要大量标记数据和计算资源。为了减少计算资源和标记数据的需求,研究人员开始研究如何融合浅层特征和深层特征以提高图像分类性能。这种融合方法可以利用浅层特征的高计算效率和深层特征的强表示能力。通过将两者结合,可以在保持较高分类准确性的同时降低计算成本和数据标记的要求。这种方法对于那些数据量较小或计算资源有限的应用场景尤为重要。通过深入研究浅层特征和深层特征的融合方法,我们可以进一
 蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM
蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM模型蒸馏是一种将大型复杂的神经网络模型(教师模型)的知识转移到小型简单的神经网络模型(学生模型)中的方法。通过这种方式,学生模型能够从教师模型中获得知识,并且在表现和泛化性能方面得到提升。通常情况下,大型神经网络模型(教师模型)在训练时需要消耗大量计算资源和时间。相比之下,小型神经网络模型(学生模型)具备更高的运行速度和更低的计算成本。为了提高学生模型的性能,同时保持较小的模型大小和计算成本,可以使用模型蒸馏技术将教师模型的知识转移给学生模型。这种转移过程可以通过将教师模型的输出概率分布作为学生
 SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PM
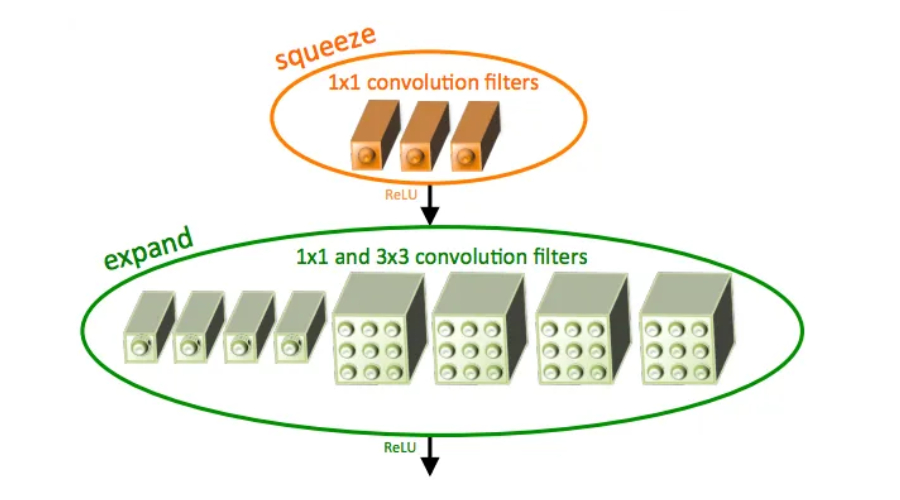
SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PMSqueezeNet是一种小巧而精确的算法,它在高精度和低复杂度之间达到了很好的平衡,因此非常适合资源有限的移动和嵌入式系统。2016年,DeepScale、加州大学伯克利分校和斯坦福大学的研究人员提出了一种紧凑高效的卷积神经网络(CNN)——SqueezeNet。近年来,研究人员对SqueezeNet进行了多次改进,其中包括SqueezeNetv1.1和SqueezeNetv2.0。这两个版本的改进不仅提高了准确性,还降低了计算成本。SqueezeNetv1.1在ImageNet数据集上的精度


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

Dreamweaver CS6
视觉化网页开发工具

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。

mPDF
mPDF是一个PHP库,可以从UTF-8编码的HTML生成PDF文件。原作者Ian Back编写mPDF以从他的网站上“即时”输出PDF文件,并处理不同的语言。与原始脚本如HTML2FPDF相比,它的速度较慢,并且在使用Unicode字体时生成的文件较大,但支持CSS样式等,并进行了大量增强。支持几乎所有语言,包括RTL(阿拉伯语和希伯来语)和CJK(中日韩)。支持嵌套的块级元素(如P、DIV),

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

Dreamweaver Mac版
视觉化网页开发工具





