详解贝尔曼福特算法并用Python实现

贝尔曼福特算法(Bellman Ford)可以找到从目标节点到加权图其他节点的最短路径。这一点和Dijkstra算法很相似，贝尔曼福特算法可以处理负权重的图，从实现来看也相对简单。

贝尔曼福特算法原理详解

贝尔曼福特算法通过高估从起始顶点到所有其他顶点的路径长度，迭代寻找比高估路径更短的新路径。

因为我们要记录每个节点的路径距离，可以将其存储在大小为n的数组中，n也代表了节点的数量。

实例图

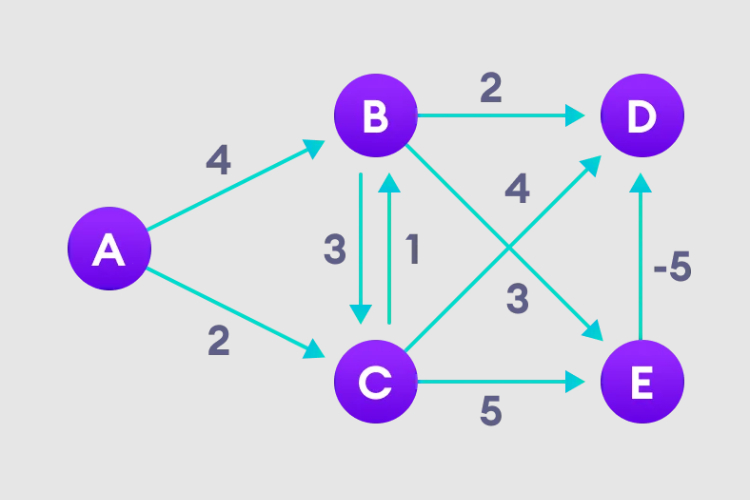
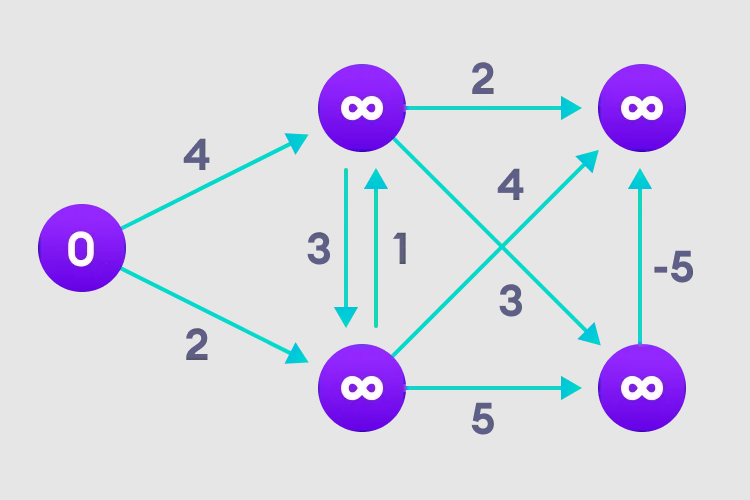
1、选择起始节点，并无限指定给其他所有顶点，记录路径值。

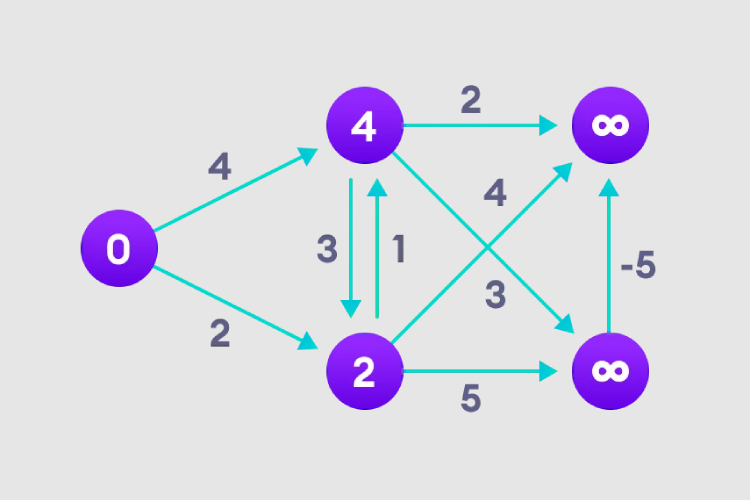
2、访问每条边，并进行松弛操作，不断更新最短路径。

3、我们需要这样做N-1次，因为在最坏的情况下，最短节点路径长度可能需要重新调整N-1次。

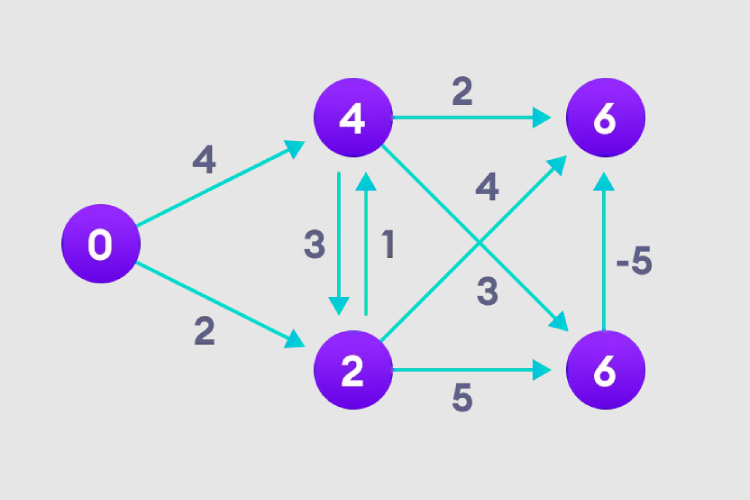
4、注意右上角的节点是如何调整其路径长度的。

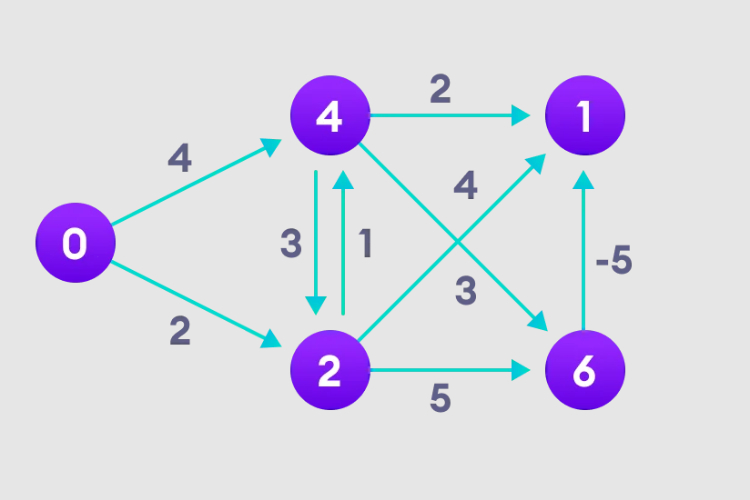
5、在所有节点都有路径长度之后，再检查是否存在负环路。

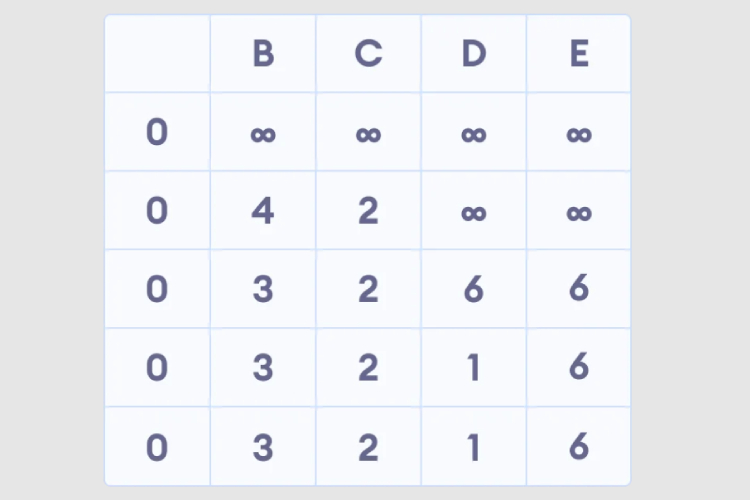
Python实现贝尔曼福特算法

class Graph:

    def __init__(self, vertices):
        self.V = vertices   # Total number of vertices in the graph
        self.graph = []     # Array of edges

    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    def print_solution(self, dist):
        print("Vertex Distance from Source")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

    def bellman_ford(self, src):

        dist = [float("Inf")] * self.V
        dist[src] = 0

        for _ in range(self.V - 1):
            for s, d, w in self.graph:
                if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                    dist[d] = dist[s] + w

        for s, d, w in self.graph:
            if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                print("Graph contains negative weight cycle")
                return

        self.print_solution(dist)

g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)

以上是详解贝尔曼福特算法并用Python实现的详细内容。更多信息请关注PHP中文网其他相关文章！