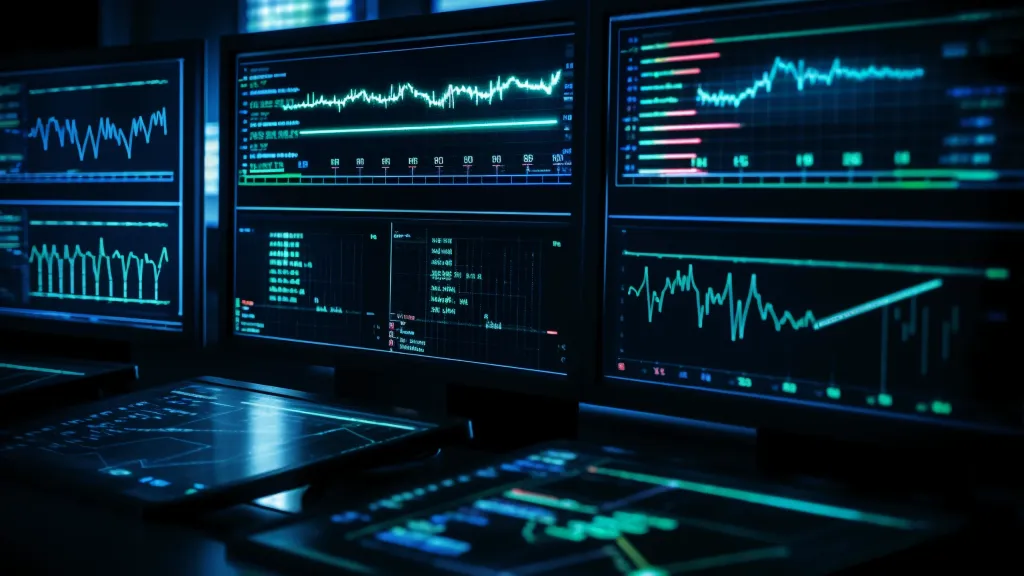
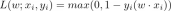累积概率分布函数(APDF)是概率密度函数的积分,用于描述随机变量X小于或等于某个值x的概率。在机器学习中,CDF被广泛应用于理解和分析数据分布,以选择适合的模型和算法进行建模和预测。通过计算CDF,我们可以得到某个值落在特定百分比范围内的概率。这有助于我们评估数据点相对于整个数据集的位置和重要性。另外,CDF还可以用于计算分位数,即将数据集划分为特定百分比的区间,从而更好地理解数据的分布情况。通过理解和分析CDF,我们能够更好地了解数据的特征,并为模型选择和预测提供指导。
从概念上理解,CDF是用来描述随机变量X的一个函数。它表示X小于或等于某个特定值x的概率。具体地说,CDF被定义为F(x)=P(X≤x),其中P表示概率。CDF的取值范围在0到1之间,并且具有单调不减的性质,也就是说随着x的增加,CDF的值不会减小。当x趋近于正无穷时,CDF趋近于1,而当x趋近于负无穷时,CDF趋近于0。
CDF是累积分布函数,用于描述随机变量的分布情况。通过对CDF求导可得到概率密度函数PDF,即f(x)=dF(x)/dx。PDF描述了随机变量在不同取值处的概率密度,可以用来计算随机变量落在某个取值区间内的概率。因此,CDF和PDF是相互关联的,可以互相转换和应用。
CDF是累积分布函数,用于分析数据的分布情况并选择适当的模型和算法进行建模和预测。如果数据的CDF呈正态分布,可以选择高斯模型。对于偏态分布或缺乏对称性的数据,可以选择非参数模型或偏态分布模型。此外,CDF还可计算统计量,如均值、方差、中位数,并进行假设检验和置信区间计算。
离散型随机变量的累积分布函数(CDF)可以通过累加概率质量函数(PMF)得到。而对于连续型随机变量,CDF可以通过积分概率密度函数(PDF)得到。计算CDF时可以利用数值积分、蒙特卡罗模拟等方法。此外,一些常见的分布(例如正态分布、t分布、F分布、卡方分布等)的CDF已经被推导出来,可以通过查表或者使用相关软件进行计算。
总之,累积分布函数在机器学习中具有重要的应用,可以帮助我们理解和分析数据的分布情况,选择合适的模型和算法进行建模和预测,计算统计量和进行假设检验和置信区间的计算等。因此,对于从事机器学习相关工作的人员来说,熟练掌握累积分布函数的概念、原理、作用和计算方法,是非常重要的。
以上是累积概率分布函数(APDF)的详细内容。更多信息请关注PHP中文网其他相关文章!
 优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM
优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM介绍 恭喜!您经营一家成功的业务。通过您的网页,社交媒体活动,网络研讨会,会议,免费资源和其他来源,您每天收集5000个电子邮件ID。下一个明显的步骤是
 Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM
Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM介绍 在当今快节奏的软件开发环境中,确保最佳应用程序性能至关重要。监视实时指标,例如响应时间,错误率和资源利用率可以帮助MAIN
 Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM“您有几个用户?”他扮演。 阿尔特曼回答说:“我认为我们上次说的是每周5亿个活跃者,而且它正在迅速增长。” “你告诉我,就像在短短几周内翻了一番,”安德森继续说道。 “我说那个私人
 pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介绍 Mistral发布了其第一个多模式模型,即Pixtral-12b-2409。该模型建立在Mistral的120亿参数Nemo 12B之上。是什么设置了该模型?现在可以拍摄图像和Tex
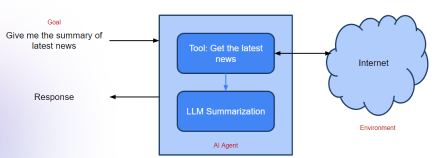 生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想象一下,拥有一个由AI驱动的助手,不仅可以响应您的查询,还可以自主收集信息,执行任务甚至处理多种类型的数据(TEXT,图像和代码)。听起来有未来派?在这个a


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

SublimeText3 Linux新版
SublimeText3 Linux最新版

EditPlus 中文破解版
体积小,语法高亮,不支持代码提示功能

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

记事本++7.3.1
好用且免费的代码编辑器