如何使用三角函数y=Asin(wx+φ)中的相位角φ

三角函数y Asinwx φ中的φ怎么

一、键点法：

确定φ值时，考虑函数y=Asin(ωx+φ)+B与x轴的交点。我们需要找到最开始与x轴相交的点的横坐标，即令ωx+φ=0。这样就可以确定φ的值。 为了选择正确的点来代入解析式，我们需要注意点属于“五点法”中的哪一个点。在“五点法”中，我们选择的是“第一点”，这是指图像上升时与x轴相交的点。因此，此时ωx+φ=0。 请注意，回答的字数不能超过112个。

“最大值点”（即图象的“峰点”）时

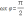
“最小值点”（即图象的“谷点”）时

二、代入法：

可以通过将已知点代入方程或求解图像与直线交点来确定A、ω和B的值。需注意交点位置。

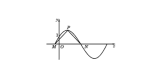
扩展资料：

三角函数y=Asin（ωx+φ）单调性的方法：

1、我们可以从复合函数的角度去理解函数y=Asin（ωx+φ）的单调性。复合函数的单调性由内层函数和外层函数共同决定的。

若在某一区间内内层函数和外层函数的单调性相同，则复合函数为增函数。若在某一区间内内层函数和外层函数的单调性相反，则复合函数为减函数。简言之，同增异减。

2、函数y=Asin（ωx+φ）的图象是由函数y=sinx经过伸缩平移变换得到的。函数y=Asin（ωx+φ）的单调性也是依据函数y=sinx解。

函数y=Asin（ωx+φ）可以看成是由函数y=sint和函数t=ωx+φ复合而成的。函数t=ωx+φ是一次函数，它的单调性由ω的正负决定。

所以我们只要把（ωx+φ）看成一个整体代入y=sint的单调区间。

例如函数y=sint的单调增区间为[-（π/2）+2kπ，（π/2）+2kπ]，则我们可以将t整体替换为ωx+φ，即-（π/2）+2kπ≤ωx+φ≤（π/2）+2kπ。

我们只需要解不等式-（π/2）+2kπ≤（ωx+φ）≤（π/2）+2kπ就可以得到函数y=Asin（ωx+φ）的单调区间。

3、为了减少分析的难度，我们一般都利用诱导公式把函数y=Asin（ωx+φ）中的ω变为正数，这样我们就能保证一次函数t=ωx+φ在实数集上为增函数。

由复合函数的性质知道，我们要函数y=Asin（ωx+φ）的单调增（减）区间则将（ωx+φ）整体带入函数y=sint的单调增（减）区间，再结合A的正负，最后解出x的范围。解出的x范围就是函数y=Asin（ωx+φ）的单调区间。

参考资料来源：百科——三角函数

直线的斜率公式

直线的斜率计算公式：k=(y2-y1)/(x2-x1)

由一条直线与右边X轴所成的角的正切。

k=tanα=（y2-y1）/(x2-x1)或（y1-y2）/(x1-x2)

当直线L的斜率存在时，对于一次函数y=kx+b（斜截式），k即该函数图像（直线）的斜率。

扩展资料

当直线L的斜率不存在时，斜截式y=kx+b 当k=0时 y=b

当直线L的斜率存在时，点斜式y2—y1=k(X2—X1),

当直线L在两坐标轴上存在非零截距时，有截距式X/a+y/b=1

对于任意函数上任意一点，其斜率等于其切线与x轴正方向的夹角，即tanα

斜率计算：ax+by+c=0中，k=-a/b.

直线斜率公式：k=(y2-y1)/(x2-x1)

两条垂直相交直线的斜率相乘积为-1:k1*k2=-1.

当k>0时，直线与x轴夹角越大，斜率越大；当k

以上是如何使用三角函数y=Asin(wx+φ)中的相位角φ的详细内容。更多信息请关注PHP中文网其他相关文章！