
数组的逆时针旋转意味着将给定数组的所有元素向左侧旋转给定的索引数。在本文中,我们将实现一个 JavaScript 程序,用于按 k 个索引逆时针旋转数组的范围求和查询。
问题简介
在这个问题中,我们得到一个包含一些整数的数组和另一个包含成对形式的值的数组。每对将是当前查询所需的旋转次数,在给定的旋转次数之后,我们将得到一个范围,并且必须回答该给定范围中存在的元素的总和。例如,
示例1
Input Given array: [1, 2, 3, 4, 5, 6] Query: [3, 1, 4] Output 14
说明
旋转次数为3,因此旋转3次后的数组为4 5 6 1 2 3。
1 到 4 范围内的元素为 5、6、1 和 2。因此,总和为 14。
示例2
Input Given array: [1, 2, 3, 4, 5, 6] Query: [8, 0, 3] Output 18
说明
旋转次数为 8,因此 8 次旋转后的数组等于 8 %(数组长度)旋转,因为在数组旋转次数的长度之后,再次出现相同的数组意味着 8 次旋转是等效的至 2 次旋转。
因此,旋转 8 次后的数组为 3 4 5 6 1 2。
在该范围内,0 到 3 个元素分别为 3、4、5 和 6。因此,总和为 18。
天真的方法
在简单的方法中,我们将简单地执行查询数组中所述的所有步骤。就像,它被赋予旋转数组,然后我们将数组元素旋转给定的次数,然后检查范围内元素的总和。让我们看看它的代码 -
示例
// function to answer the queries
function getSum(arr, rotations, L, R){
var len = arr.length
var rot = rotations % len;
var temp = new Array(len);
// rotating the given array
for(var i =0; i< len - rot; i++ ){
temp[i] = arr[i + rot];
}
// getting the last elements
for(var i = 0; i < rot; i++) {
temp[len-rot+i] = arr[i];
}
// getting the required sum
var sum = 0;
for(var i = L; i<=R; i++){
sum += temp[i];
}
console.log("The sum of the elements in the range " + L + " to " + R + " after " + rotations + " number of rotations is " + sum);
}
// defining the array
var arr = [ 1, 2, 3, 4, 5, 6]
// defining the queries array
var queries = [ [ 3, 1, 4], [ 8, 0, 3]]
// traversing over the given array
for(var i = 0; i<queries.length; i++){
getSum(arr, queries[i][0], queries[i][1], queries[i][2]);
}
时间和空间复杂度
上述代码的时间复杂度为 O(Q*N),其中 Q 是查询次数,N 是数组大小。
上述代码的时间复杂度为 O(N),因为我们正在创建一个大小为 N 的新数组。
前缀和法
在前缀和方法中,我们将创建一个前缀和数组,并且前缀和数组的每个索引包含截至当前索引的所有元素的总和。让我们看看它的代码 -
示例
// function to answer the queries
function getSum(preSum, rotations, L, R){
var len = preSum.length
var rot = rotations % len;
// updating L and R
L = (L + rot) %len
R = (R + rot) %len
var sum = 0;
if(L <= R) {
if(L == 0) {
sum = preSum[R];
}
else{
sum = preSum[R]-preSum[L-1];
}
}
else{
sum += preSum[R];
sum += preSum[len-1]-preSum[L-1];
}
console.log("The sum of the elements in the range " + L + " to " + R + " after " + rotations + " number of rotations is " + sum);
}
// defining the array
var arr = [ 1, 2, 3, 4, 5, 6]
var preSum = new Array(arr.length)
preSum[0] = arr[0]
for(var i = 1; i<arr.length; i++){
preSum[i] = preSum[i-1] + arr[i]
}
// defining the quries array
var queries = [ [ 3, 1, 4], [ 8, 0, 3]]
// traversing over the given array
for(var i = 0; i<queries.length; i++){
getSum(preSum, queries[i][0], queries[i][1], queries[i][2]);
}
时间和空间复杂度
上述代码的时间复杂度为 O(Q),其中 Q 是查询数量。
上述代码的时间复杂度为 O(N),因为我们正在创建一个新数组来存储数组元素的前缀和。
结论
在本教程中,我们实现了一个 JavaScript 程序,用于按 k 索引逆时针旋转数组的范围求和查询。数组逆时针旋转意味着将给定数组的所有元素向左侧旋转给定数量的索引。我们首先实现了两种方法,一种是时间复杂度为 O(Q*N) 的朴素方法,另一种是时间复杂度为 O(Q) 的前缀和方法。
以上是用于按 K 索引逆时针旋转数组的范围求和查询的 JavaScript 程序的详细内容。更多信息请关注PHP中文网其他相关文章!
 在JavaScript中替换字符串字符Mar 11, 2025 am 12:07 AM
在JavaScript中替换字符串字符Mar 11, 2025 am 12:07 AMJavaScript字符串替换方法详解及常见问题解答 本文将探讨两种在JavaScript中替换字符串字符的方法:在JavaScript代码内部替换和在网页HTML内部替换。 在JavaScript代码内部替换字符串 最直接的方法是使用replace()方法: str = str.replace("find","replace"); 该方法仅替换第一个匹配项。要替换所有匹配项,需使用正则表达式并添加全局标志g: str = str.replace(/fi
 构建您自己的Ajax Web应用程序Mar 09, 2025 am 12:11 AM
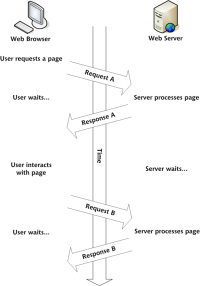
构建您自己的Ajax Web应用程序Mar 09, 2025 am 12:11 AM因此,在这里,您准备好了解所有称为Ajax的东西。但是,到底是什么? AJAX一词是指用于创建动态,交互式Web内容的一系列宽松的技术。 Ajax一词,最初由Jesse J创造
 如何在浏览器中优化JavaScript代码以进行性能?Mar 18, 2025 pm 03:14 PM
如何在浏览器中优化JavaScript代码以进行性能?Mar 18, 2025 pm 03:14 PM本文讨论了在浏览器中优化JavaScript性能的策略,重点是减少执行时间并最大程度地减少对页面负载速度的影响。
 jQuery矩阵效果Mar 10, 2025 am 12:52 AM
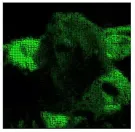
jQuery矩阵效果Mar 10, 2025 am 12:52 AM将矩阵电影特效带入你的网页!这是一个基于著名电影《黑客帝国》的酷炫jQuery插件。该插件模拟了电影中经典的绿色字符特效,只需选择一张图片,插件就会将其转换为充满数字字符的矩阵风格画面。快来试试吧,非常有趣! 工作原理 插件将图片加载到画布上,读取像素和颜色值: data = ctx.getImageData(x, y, settings.grainSize, settings.grainSize).data 插件巧妙地读取图片的矩形区域,并利用jQuery计算每个区域的平均颜色。然后,使用
 如何使用浏览器开发人员工具有效调试JavaScript代码?Mar 18, 2025 pm 03:16 PM
如何使用浏览器开发人员工具有效调试JavaScript代码?Mar 18, 2025 pm 03:16 PM本文讨论了使用浏览器开发人员工具的有效JavaScript调试,专注于设置断点,使用控制台和分析性能。
 如何构建简单的jQuery滑块Mar 11, 2025 am 12:19 AM
如何构建简单的jQuery滑块Mar 11, 2025 am 12:19 AM本文将引导您使用jQuery库创建一个简单的图片轮播。我们将使用bxSlider库,它基于jQuery构建,并提供许多配置选项来设置轮播。 如今,图片轮播已成为网站必备功能——一图胜千言! 决定使用图片轮播后,下一个问题是如何创建它。首先,您需要收集高质量、高分辨率的图片。 接下来,您需要使用HTML和一些JavaScript代码来创建图片轮播。网络上有很多库可以帮助您以不同的方式创建轮播。我们将使用开源的bxSlider库。 bxSlider库支持响应式设计,因此使用此库构建的轮播可以适应任何
 如何使用Angular上传和下载CSV文件Mar 10, 2025 am 01:01 AM
如何使用Angular上传和下载CSV文件Mar 10, 2025 am 01:01 AM数据集对于构建API模型和各种业务流程至关重要。这就是为什么导入和导出CSV是经常需要的功能。在本教程中,您将学习如何在Angular中下载和导入CSV文件


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

SublimeText3 英文版
推荐:为Win版本,支持代码提示!

SecLists
SecLists是最终安全测试人员的伙伴。它是一个包含各种类型列表的集合,这些列表在安全评估过程中经常使用,都在一个地方。SecLists通过方便地提供安全测试人员可能需要的所有列表,帮助提高安全测试的效率和生产力。列表类型包括用户名、密码、URL、模糊测试有效载荷、敏感数据模式、Web shell等等。测试人员只需将此存储库拉到新的测试机上,他就可以访问到所需的每种类型的列表。

Dreamweaver Mac版
视觉化网页开发工具

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。

SublimeText3 Linux新版
SublimeText3 Linux最新版







