C程序中的Peterson图问题
- PHPz转载
- 2023-08-26 11:01:10973浏览
假设我们有一个如下所示的图形。这个图形是彼得森图。顶点从0到9编号。每个顶点都有一些字母。考虑一个在该图中的行走W,其中使用了L个顶点。当行走W中的字母序列和S相同时,字符串S由行走W实现。我们可以多次访问顶点。
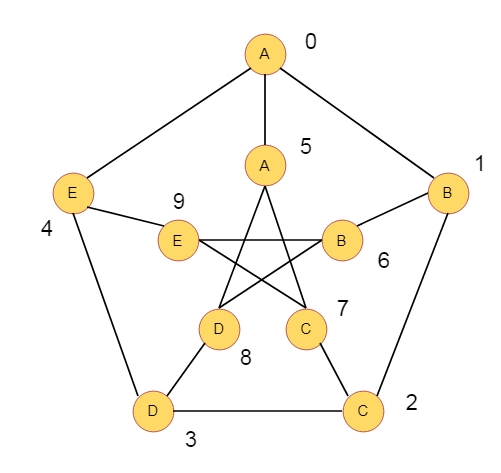
例如,一个字符串S类似于“ABBECCD”,这由行走(0, 1, 6, 9, 7, 2, 3)实现。我们的任务是找到这样的行走,并且如果存在这样的行走,则找到字典顺序最小的行走。如果没有这样的行走,则返回-1。
算法
petersonGraphWalk(S, v) -
begin
res := starting vertex
for each character c in S except the first one, do
if there is an edge between v and c in outer graph, then
v := c
else if there is an edge between v and c+5 in inner graph, then
v := c + 5
else
return false
end if
put v into res
done
return true
endExample
的中文翻译为:示例
#include<iostream>
using namespace std;
bool adj_mat[10][10] = {{0, 1, 0, 0, 1, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0, 0, 0, 1, 0},
{1, 0, 0, 1, 0, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 0, 1, 1, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 1, 1},
{0, 0, 1, 0, 0, 1, 0, 0, 0, 1},
{0, 0, 0, 1, 0, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 1, 1, 0, 0}
};
char S[100005];
char res[100005];
bool petersonGraphWalk(char* S, int v){
res[0] = v + '0';
for(int i = 1; S[i]; i++){
//traverse the outer graph
if(adj_mat[v][S[i] - 'A'] || adj_mat[S[i] - 'A'][v]){
v = S[i] - 'A';
}
//then check the inner graph
else if(adj_mat[v][S[i] - 'A' + 5] || adj_mat[S[i] - 'A' + 5][v]){
v = S[i] - 'A' + 5;
}else{
return false;
}
res[i] = v + '0';
}
return true;
}
main() {
char* str = "ABBECCD";
if(petersonGraphWalk(str, str[0] - 'A') || petersonGraphWalk(str, str[0] - 'A' + 5)){
cout << res;
}else{
cout << -1;
}
}输出
0169723
以上是C程序中的Peterson图问题的详细内容。更多信息请关注PHP中文网其他相关文章!
声明:
本文转载于:tutorialspoint.com。如有侵权,请联系admin@php.cn删除

