Python怎么调用实现最小二乘法

所谓线性最小二乘法，可以理解为是解方程的延续，区别在于，当未知量远小于方程数的时候，将得到一个无解的问题。最小二乘法的实质，是保证误差最小的情况下对未知数进行赋值。

最小二乘法是非常经典的算法，而且这个名字我们在高中的时候就已经接触了，属于极其常用的算法。此前曾经写过线性最小二乘法的原理，并用Python实现：最小二乘法及其Python实现；以及scipy中非线性最小二乘法的调用方式：非线性最小二乘法（文末补充内容）；还有稀疏矩阵的最小二乘法：稀疏矩阵最小二乘法。

下面讲对numpy和scipy中实现的线性最小二乘法进行说明，并比较二者的速度。

numpy实现

numpy中便实现了最小二乘法，即lstsq(a,b)用于求解类似于a@x=b中的x，其中，a为M×N的矩阵；则当b为M行的向量时，刚好相当于求解线性方程组。对于Ax=b这样的方程组，如果A是满秩仿真，那么可以表示为x=A⁻¹b，否则可以表示为x=(A^TA)⁻¹A^Tb。

当b为M×K的矩阵时，则对每一列，都会计算一组x。

其返回值共有4个，分别是拟合得到的x、拟合误差、矩阵a的秩、以及矩阵a的单值形式。

import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]

scipy封装

scipy.linalg同样提供了最小二乘法函数，函数名同样是lstsq，其参数列表为

lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

其中a, b即Ax=b，二者均提供可覆写开关，设为True可以节省运行时间，此外，函数也支持有限性检查，这是linalg中许多函数都具备的选项。其返回值与numpy中的最小二乘函数相同。

cond为浮点型参数，表示奇异值阈值，当奇异值小于cond时将舍弃。

lapack_driver为字符串选项，表示选用何种LAPACK中的算法引擎，可选'gelsd', 'gelsy', 'gelss'。

import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]

速度对比

最后，对着两组最小二乘函数做一个速度上的对比

from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807

这一次，二者并没有拉开太大的差距，即使将矩阵维度放大到500，二者也是半斤八两。

N = 500
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173

补充

Python调用非线性最小二乘法

简介与构造函数

在scipy中，非线性最小二乘法的目的是找到一组函数，使得误差函数的平方和最小，可以表示为如下公式

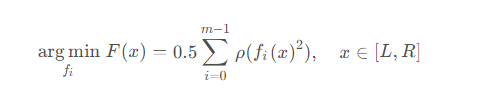
其中ρ表示损失函数，可以理解为对f_i(x)的一次预处理。

scipy.optimize中封装了非线性最小二乘法函数least_squares，其定义为

least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs)

其中，func和x0为必选参数，func为待求解函数，x0为函数输入的初值，这两者无默认值，为必须输入的参数。

bound为求解区间，默认(−∞,∞)，verbose为1时，会有终止输出，为2时会print更多的运算过程中的信息。此外下面几个参数用于控制误差，比较简单。

	默认值	备注
ftol	10-8	函数容忍度
xtol	10-8	自变量容忍度
gtol	10-8	梯度容忍度
x_scale	1.0	变量的特征尺度
f_scale	1.0	残差边际值

loss为损失函数，就是上面公式中的ρ \rhoρ，默认为linear，可选值包括

迭代策略

上面的公式仅给出了算法的目的，但并未暴露其细节。关于如何找到最小值，则需要确定搜索最小值的方法，method为最小值搜索的方案，共有三种选项，默认为trf

• trf：即Trust Region Reflective，信赖域反射算法

• dogbox：信赖域狗腿算法

• lm：Levenberg-Marquardt算法

这三种方法都是信赖域方法的延申，信赖域的优化思想其实就是从单点的迭代变成了区间的迭代，由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数，故而仅对其原理做简略的介绍。

其中r为置信半径，假设在这个邻域内，目标函数可以近似为线性或二次函数，则可通过二次模型得到区间中的极小值点s_k。然后以这个极小值点为中心，继续优化信赖域所对应的区间。

雅可比矩阵

在了解了信赖域方法之后，就会明白雅可比矩阵在数值求解时的重要作用，而如何计算雅可比矩阵，则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法，主要提供了三种方案，分别是基于两点的2-point；基于三点的3-point；以及基于复数步长的cs。一般来说，三点的精度高于两点，但速度也慢一倍。

此外，可以输入自定义函数来计算雅可比矩阵。

测试

最后，测试一下非线性最小二乘法

import numpy as np
from scipy.optimize import least_squares

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
    return _sum

x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
'''
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
'''

以上是Python怎么调用实现最小二乘法的详细内容。更多信息请关注PHP中文网其他相关文章！