Python递归下降Parser怎么实现

1. 算术运算表达式求值

要解析这类文本，需要另外一种特定的语法规则。我们这里介绍可以表示上下文无关文法（context free grammer）的语法规则巴科斯范式(BNF)和扩展巴科斯范式(EBNF)。从小到一个算术运算表达式，到大到几乎所有程序设计语言，都是利用上下文无关文法来定义的。

对于简单的算术运算表达式，假定我们已经用分词技术将其转化为输入的tokens流，如NUM+NUM*NUM（分词方法参见上一篇博文）。

在此基础上，我们定义BNF规则定义如下：

expr ::= expr + term
     | expr - term 
     | term
term ::= term * factor
     | term / factor
     | factor
factor ::= (expr)
     | NUM

当然，这种计法还不够简洁明了，我们实际采用的为EBNF形式：

expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr) 
       | NUM

BNF和EBNF每一条规则(形如::=的式子)都可以看做是一种替换，即左侧的符号可以被右侧的符号所替换。我们在解析过程中尝试使用BNF/EBNF将输入文本与语法规则进行匹配，以完成各种替换和扩展。在EBNF中，被放置在{...}*内的规则是可选的，而*则表示可以重复零次或多次（类比于正则表达式）。

下图形象地展示了递归下降解析器(parser)中“递归”和“下降”部分和ENBF的关系：

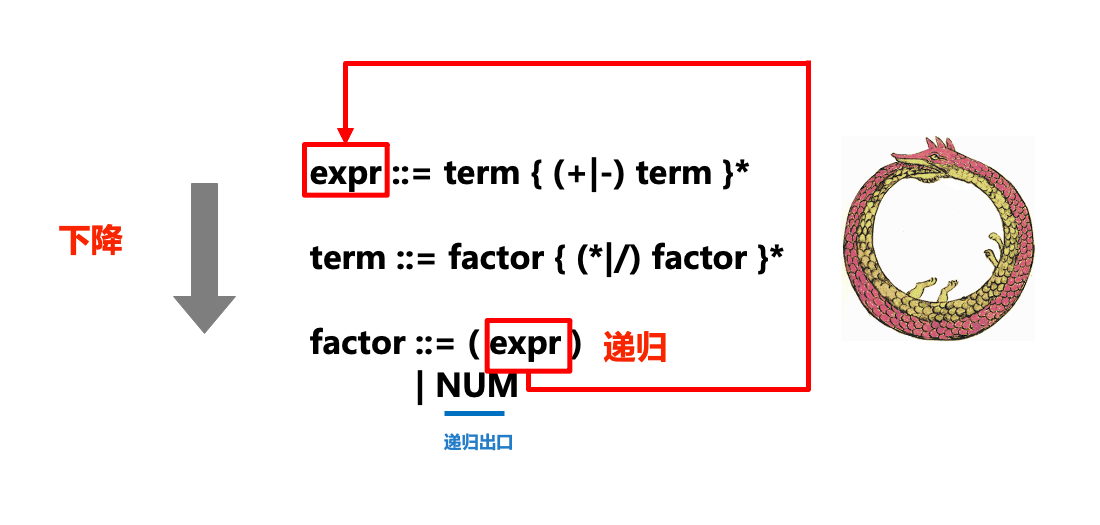
在实际的解析过程中，我们对tokens流从左到右进行扫描，在扫描的过程中处理token，如果卡住就产生一个语法错误。每一条语法规则都被转化为一个函数或方法，例如上面的ENBF规则被转换成下述方法：

class ExpressionEvaluator():
    ...
    def expr(self):
        ...
    def term(self):
        ...
    def factor(self):
        ...

在调用某个规则对应方法的过程中，如果我们发现接下来的符号需要采用另一个规则来匹配，则我们就会“下降”到另一个规则方法（如在expr中调用term，term中调用factor），则也就是递归下降中“下降”的部分。

有时也会调用已经在执行的方法（比如在expr中调用term，term中调用factor后，又在factor中调用expr，相当于一条衔尾蛇），这也就是递归下降中“递归”的部分。

对于语法中出现的重复部分（例如expr ::= term { (+|-) term }*），我们则通过while循环来实现。

下面我们来看具体的代码实现。首先是分词部分，我们参照上一篇介绍分词博客的代码。

import re
import collections

# 定义匹配token的模式
NUM = r&#39;(?P<NUM>\d+)&#39;  # \d表示匹配数字，+表示任意长度
PLUS = r&#39;(?P<PLUS>\+)&#39;  # 注意转义
MINUS = r&#39;(?P<MINUS>-)&#39;
TIMES = r&#39;(?P<TIMES>\*)&#39;  # 注意转义
DIVIDE = r&#39;(?P<DIVIDE>/)&#39;
LPAREN = r&#39;(?P<LPAREN>\()&#39;  # 注意转义
RPAREN = r&#39;(?P<RPAREN>\))&#39;  # 注意转义
WS = r&#39;(?P<WS>\s+)&#39;  # 别忘记空格，\s表示空格，+表示任意长度

master_pat = re.compile(
    &#39;|&#39;.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))

# Tokenizer
Token = collections.namedtuple(&#39;Token&#39;, [&#39;type&#39;, &#39;value&#39;])


def generate_tokens(text):
    scanner = master_pat.scanner(text)
    for m in iter(scanner.match, None):
        tok = Token(m.lastgroup, m.group())
        if tok.type != &#39;WS&#39;:  # 过滤掉空格符
            yield tok

下面是表达式求值器的具体实现：

class ExpressionEvaluator():
    """ 递归下降的Parser实现，每个语法规则都对应一个方法，
    使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
    使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
    """

    def parse(self, text):
        """ 对外调用的接口 """
        self.tokens = generate_tokens(text)
        self.tok, self.next_tok = None, None  # 已匹配的最后一个token，下一个即将匹配的token
        self._next()  # 转到下一个token
        return self.expr()  # 开始递归

    def _next(self):
        """ 转到下一个token """
        self.tok, self.next_tok = self.next_tok, next(self.tokens, None)

    def _accept(self, tok_type):
        """ 如果下一个token与tok_type匹配，则转到下一个token """
        if self.next_tok and self.next_tok.type == tok_type:
            self._next()
            return True
        else:
            return False

    def _except(self, tok_type):
        """ 检查是否匹配，如果不匹配则抛出异常 """
        if not self._accept(tok_type):
            raise SyntaxError("Excepted"+tok_type)

    # 接下来是语法规则，每个语法规则对应一个方法
    
    def expr(self):
        """ 对应规则： expression ::= term { ('+'|'-') term }* """
        exprval = self.term() # 取第一项
        while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type 
            # 再取下一项，即运算符右值
            right = self.term() 
            if op == "PLUS":
                exprval += right
            elif op == "MINUS":
                exprval -= right
        return exprval
            
    def term(self):
        """ 对应规则： term ::= factor { ('*'|'/') factor }* """
        
        termval = self.factor() # 取第一项
        while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type 
            # 再取下一项，即运算符右值
            right = self.factor() 
            if op == "TIMES":
                termval *= right
            elif op == "DIVIDE":
                termval /= right
        return termval          
            
        
    def factor(self):
        """ 对应规则： factor ::= NUM | ( expr ) """
        if self._accept("NUM"): # 递归出口
            return int(self.tok.value)
        elif self._accept("LPAREN"):
            exprval = self.expr() # 继续递归下去求表达式值
            self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
            return exprval
        else:
            raise SyntaxError("Expected NUMBER or LPAREN")

我们输入以下表达式进行测试：

e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))

求值结果如下：

2
5
14
37

如果我们输入的文本不符合语法规则：

print(e.parse("2 + (3 + * 4)"))

则会抛出SyntaxError异常：Expected NUMBER or LPAREN。
综上，可见我们的表达式求值算法运行正确。

2. 生成表达式树

上面我们是得到表达式的结果，但是如果我们想分析表达式的结构，生成一棵简单的表达式解析树呢？那么我们需要对上述类的方法做一定修改：

class ExpressionTreeBuilder(ExpressionEvaluator):
    def expr(self):
            """ 对应规则： expression ::= term { ('+'|'-') term }* """
            exprval = self.term() # 取第一项
            while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
                op = self.tok.type 
                # 再取下一项，即运算符右值
                right = self.term() 
                if op == "PLUS":
                    exprval = ('+', exprval, right)
                elif op == "MINUS":
                    exprval -= ('-', exprval, right)
            return exprval
    
    def term(self):
        """ 对应规则： term ::= factor { ('*'|'/') factor }* """
        
        termval = self.factor() # 取第一项
        while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type 
            # 再取下一项，即运算符右值
            right = self.factor() 
            if op == "TIMES":
                termval = ('*', termval, right)
            elif op == "DIVIDE":
                termval = ('/', termval, right)
        return termval          
    
    def factor(self):
        """ 对应规则： factor ::= NUM | ( expr ) """
        if self._accept("NUM"): # 递归出口
            return int(self.tok.value) # 字符串转整形
        elif self._accept("LPAREN"):
            exprval = self.expr() # 继续递归下去求表达式值
            self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
            return exprval
        else:
            raise SyntaxError("Expected NUMBER or LPAREN")

输入下列表达式测试一下：

print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))

以下是生成结果：

('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)

可以看到表达式树生成正确。

我们上面的这个例子非常简单，但递归下降的解析器也可以用来实现相当复杂的解析器，例如Python代码就是通过一个递归下降解析器解析的。您要是对此跟感兴趣可以检查Python源码中的Grammar文件来一探究竟。然而，下面我们接着会看到，自己动手写一个解析器会面对各种陷阱和挑战。

左递归和运算符优先级陷阱

任何涉及左递归形式的语法规则，都没法用递归下降parser来解决。所谓左递归，即规则式子右侧最左边的符号是规则头，比如对于以下规则：

items ::= items ',' item 
      | item

完成该解析你可能会定义以下方法：

def items(self):
    itemsval = self.items() # 取第一项，然而此处会无穷递归！
    if itemsval and self._accept(','):
        itemsval.append(self.item())
    else:
        itemsval = [self.item()]

这样做会在第一行就无穷地调用self.items()从而产生无穷递归错误。

还有一种是语法规则自身的错误，比如运算符优先级。我们如果忽视运算符优先级直接将表达式简化如下：

expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
       | NUM

PYTHON 复制 全屏

这个语法从技术上可以实现，但是没有遵守计算顺序约定，导致"3+4*5"的运算结果为35，而不是预期的23。因此，需要使用单独的expr和term规则来确保计算结果的正确性。

以上是Python递归下降Parser怎么实现的详细内容。更多信息请关注PHP中文网其他相关文章！