AI再卷数学界,DSP新方法将机器证明成功率提高一倍
- PHPz转载
- 2023-05-13 13:43:061667浏览
自动证明数学定理是人工智能的一个初衷,也是一直以来的难题。到目前为止,人类数学家使用了两种不同的方式来书写数学。
第一种是大家都熟悉的方式,即用自然语言来描述数学证明。大部分的数学都是以这种方式书写的,这包括数学课本,数学论文,等等。
第二种称之为形式化数学(formal mathematics)。这是近半个世纪计算机科学家创造的,用来检验数学证明的一种工具。
如今看来,计算机可以被用来验证数学证明,但它们只有在使用专门设计的证明语言时才能做到这一点,而无法处理数学符号和数学家使用的书面文本的混合体。如果把用自然语言编写的数学问题转换为形式化代码,让计算机更容易解决它们,或许能够帮助构建能探索数学新发现的机器。这个过程被称为形式化(formalisation),自动形式化(autoformalization)指的是自动从自然语言数学翻译成形式化语言的任务。
形式化证明的自动化是一项具有挑战性的任务,深度学习方法在该领域尚未大获成功,这主要是因为形式化数据的稀缺。事实上,形式化证明本身是非常困难的,且只有少数专家能做到,这使得大规模的注释工作并不现实。最大的形式化证明语料库是用 Isabelle 代码 (Paulson, 1994) 编写的,大小不到 0.6GB,比视觉或自然语言处理中常用的数据集小几个数量级。为了解决形式证明的稀缺性,以往的研究提出使用合成数据、自监督或强化学习来合成额外的形式化训练数据。虽然这些方法在一定程度上缓解了数据的不足,但都无法将大量人工撰写的数学证明充分利用起来。
我们以语言模型 Minerva为例。当在足够多的数据训练之后,我们发现它的数学能力非常强,可以在高中数学测试中拿到高于平均分水平。然而这样的语言模型也有不足,它只能模仿,而不能自主训练而提高数学水平。形式化证明系统提供了一个训练环境,但形式化数学的数据非常少。
与形式化的数学不同,非形式化的数学数据是丰富和广泛可用的。最近,在非形式化数学数据上训练的大型语言模型展示了令人印象深刻的定量推理能力。然而,它们经常产生错误的证明,而自动检测这些证明中的错误推理是很有挑战性的。
在最近的一项工作中,谷歌的吴宇怀 (Yuhuai Tony Wu)等研究者设计了一种叫做 DSP(Draft, Sketch, and Prove )的新方法,将非形式化的数学证明转化为形式化的证明,从而同时具备形式化系统提供的逻辑严谨性和大量的非形式化数据。

论文链接:https://arxiv.org/pdf/2210.12283.pdf
今年早些时候,吴宇怀与几位合作者使用了 OpenAI Codex 的神经网络进行自动形式化工作,证明了用大型语言模型将非形式化语句自动翻译成形式化语句的可行性。DSP 则更进一步,利用大型语言模型从非形式化证明中生成形式化证明草图。证明草图由高层次的推理步骤组成,可以由交互式定理证明器这样的形式化系统来解释。它们与完整的形式化证明不同,因为它们包含无理由的中间猜想的序列。在 DSP 的最后一步,形式化证明草图被阐述为一个完整的形式化证明,使用一个自动验证器来证明所有中间猜想。
吴宇怀表示:现在,我们展示了 LLM 可以将其生成的非形式化证明转化为经过验证的形式化证明!
方法
方法部分描述了用于形式化证明自动化的 DSP方法,该方法利用非形式化证明来指导自动形式化定理证明器的证明草图。这里假设每个问题都有一个非形式化命题和一个描述该问题的形式化命题。整体 pipeline 包括三个阶段(如图 1 所示)。
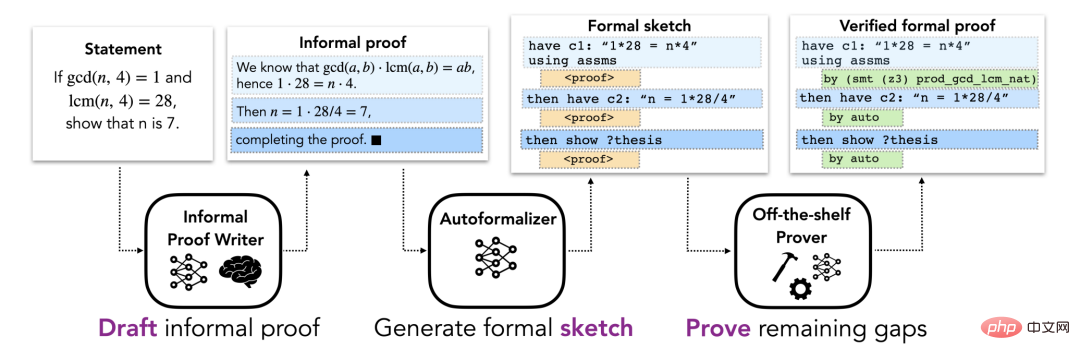
图 1.
非形式化证明的起草
DSP 方法的初始阶段,包括根据问题的自然数学语言描述(可能用 LATEX)为其寻找非形式化证明。由此产生的非形式化证明被看作是后续阶段的草稿。在数学教科书中,一般都会提供定理的证明,但有时会缺失或不完整。因此,研究者考虑了与非形式化证明的存在或不存在相对应的两种情况。
在第一种情况下,研究者假设有一个「真实的」非形式化证明(即由人写的证明),这是现有数学理论形式化实践中的典型情况。在第二种情况下,研究者做了一个更普遍的假设,即没有给出真实的非形式化证明,并且用一个经过非形式化数学数据训练的大型语言模型来起草证明候选。该语言模型消除了对人类证明的依赖,并能为每个问题产生多种备选解决方案。虽然没有简单的方法来自动验证这些证明的正确性,但非形式化证明只需要在下一阶段对生成一个好的形式化证明草图有用。
将非形式化证明映射为形式化草图
形式化证明草图对解决方案的结构进行编码,并撇开低层次的细节。直观地说,它是一个部分证明,概述了高层次的猜想命题。图 2 是一个证明草图的具体例子。尽管非形式化证明经常撇开低层次的细节,这些细节不能在形式化证明中排出,这使得非形式化证明到形式化证明的直接转换变得困难。相反,本文建议将非形式化证明映射到共享相同高层结构的形式化证明草图上。证明草图中缺少的低层次细节可以由自动证明器来填补。由于大型非形式化 - 形式化平行语料库不存在,标准的机器翻译方法不适合这项任务。相反,这里使用一个大型语言模型的小样本学习能力。具体来说,用了一些包含非形式化证明及其相应的形式化草图的例子对来 prompt 该模型,然后是一个有待转换的非形式化证明,然后让模型生成后续的 token,以获得所需的形式化草图。这个模型称为「自动形式化器」。

图 2.
证明草图中的公开猜想
作为这个过程的最后一部分,研究者执行现成的自动证明器来填补证明草图中缺失的细节,这里的「自动证明器」是指能够产生形式上可验证的证明的系统。该框架对自动证明器的具体选择是不可知的:它可以是符号证明器(如启发式证明自动化工具)、基于神经网络的证明器或者混合方法。如果自动证明器成功地填补了证明草图中的所有空白,它就会返回最终的形式化证明,可以对照问题的规格进行检查。如果自动证明器失败(例如,它超过了分配的时间限制),则认为评估是不成功的。
实验
研究者进行了一系列实验,包括从 miniF2F 数据集中生成问题的形式化证明,并表明很大一部分定理可以用这种方法自动证明。此处研究了两种环境,其中非形式化证明是由人类写的,或者是由一个在数学文本上训练的大型语言模型起草的。这两种设置对应于现有理论形式化过程中经常出现的情况,即通常有非形式化证明,但有时作为练习留给读者,或者由于空白处的限制而缺失。
表 1 展示了在 miniF2F 数据集上发现的成功形式化证明的比例。结果包括本文实验的四条 baseline,以及带有人类编写的证明和模型生成的证明的 DSP 方法。
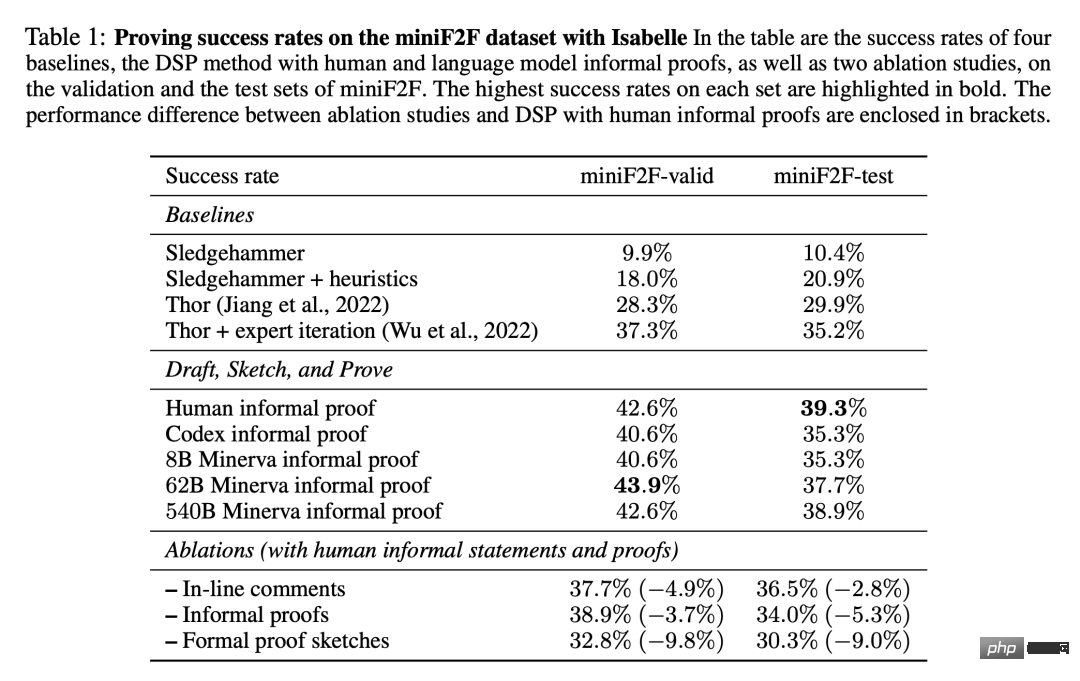
可以看出,附加了 11 种启发式策略的自动证明器大大增加了 Sledgehammer 的性能,在 miniF2F 的验证集上将其成功率从 9.9% 提高到 18.0%,在测试集上从 10.4% 提高到 20.9%。两个使用语言模型和证明搜索的 baseline 在 miniF2F 的测试集上分别达到 29.9% 和 35.2% 的成功率。
基于人类编写的非形式化证明,DSP 方法在 miniF2F 的验证和测试集上取得了 42.6% 和 39.3% 的成功率。488 个问题中共有 200 个可以通过这种方式进行证明。Codex 模型和 Minerva(8B)模型在解决 miniF2F 上的问题时给出了非常相似的结果:它们都指导自动验证器分别解决了验证集和测试集上 40.6% 和 35.3% 的问题。
当切换到 Minerva(62B)模型时,成功率分别上升到 43.9% 和 37.7%。与人编写的非形式化证明相比,其在验证集上的成功率要高 1.3%,在测试集上要低 1.6%。总的来说,Minerva(62B)模型能够解决 miniF2F 上的 199 个问题,比用人编写的证明少一个。Minerva(540B)模型在 miniF2F 的验证集和测试集中分别解决了 42.6% 和 38.9% 的问题,也生成了 199 个成功的证明。
在两种情况下,DSP 方法都能有效地指导自动证明器:使用人类的非形式化证明或语言模型生成的非形式化证明。DSP 几乎将证明器的成功率提高了一倍,并在使用 Isabelle 的 miniF2F 上产生了 SOTA 性能。此外,更大的 Minerva 模型在指导自动形式化证明器方面几乎和人类一样有帮助。
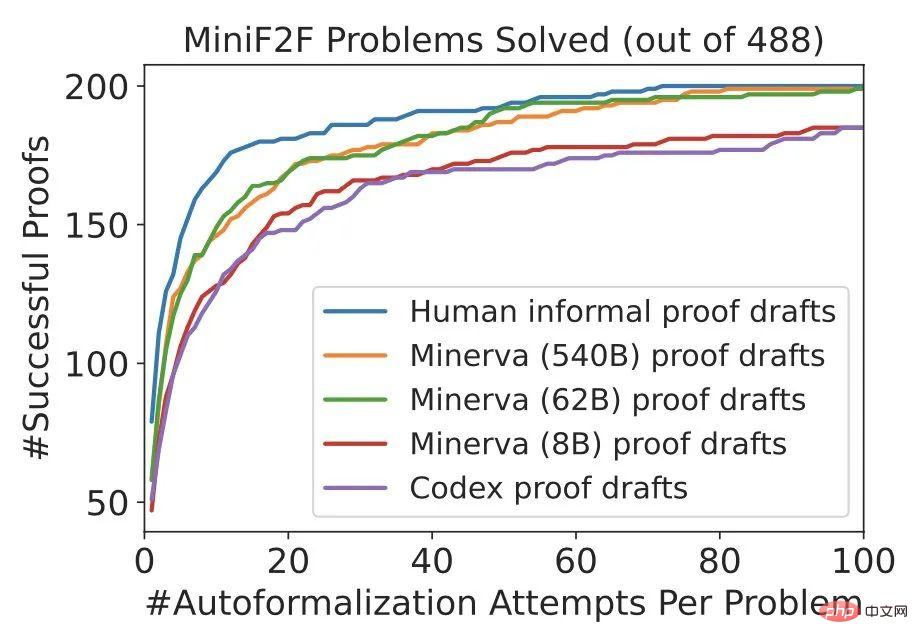
如下图所示,DSP 方法显着提高了 Sledgehammer + 启发式证明器的性能(~20% -> ~40%),在 miniF2F 上实现了新的 SOTA。
Minerva 的 62B 和 540B 版本生成的证明与人类的证明非常相似。
更多内容,请参考原论文。
以上是AI再卷数学界,DSP新方法将机器证明成功率提高一倍的详细内容。更多信息请关注PHP中文网其他相关文章!

