线性回归
1.线性回归函数
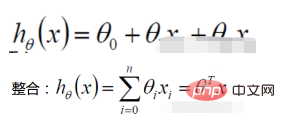
似然函数的定义:给定联合样本值X下关于(未知)参数
的函数
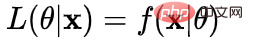

似然函数:什么样的参数跟我们的数据组合后恰好是真实值
2.线性回归似然函数
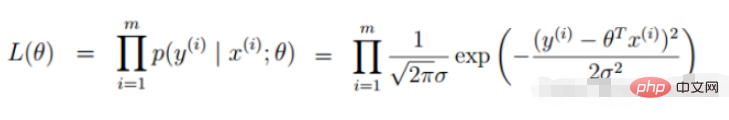
对数似然:
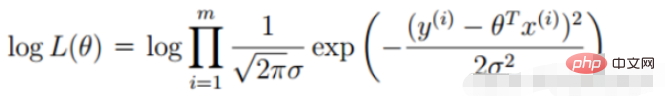
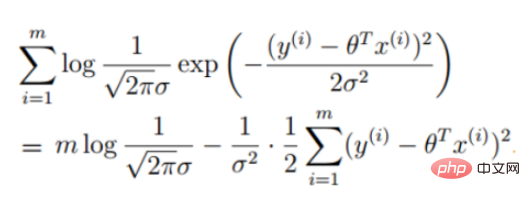
3.线性回归目标函数
(误差的表达式,我们的目的就是使得真实值与预测值之前的误差最小)
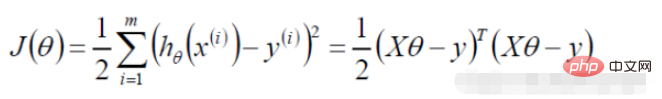
(导数为0取得极值,得到函数的参数)
逻辑回归
逻辑回归是在线性回归的结果外加一层Sigmoid函数
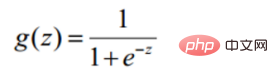
1.逻辑回归函数
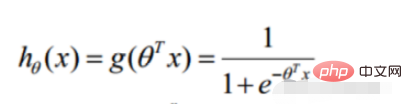
2.逻辑回归似然函数
前提数据服从伯努利分布
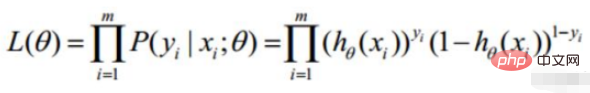
对数似然:
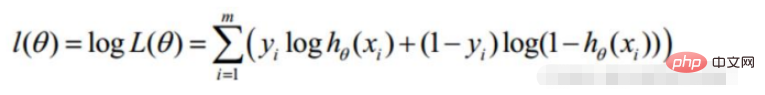
引入 转变为梯度下降任务,逻辑回归目标函数
转变为梯度下降任务,逻辑回归目标函数
梯度下降法求解
我的理解就是求导更新参数,达到一定条件后停止,得到近似最优解
代码实现
Sigmoid函数
def sigmoid(z): return 1 / (1 + np.exp(-z))
预测函数
def model(X, theta):
return sigmoid(np.dot(X, theta.T))目标函数
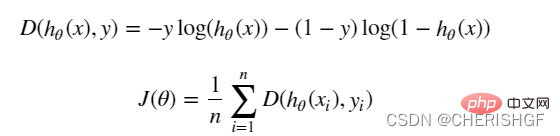
def cost(X, y, theta):
left = np.multiply(-y, np.log(model(X, theta)))
right = np.multiply(1 - y, np.log(1 - model(X, theta)))
return np.sum(left - right) / (len(X))梯度
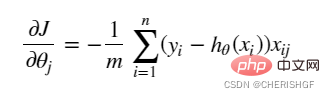
def gradient(X, y, theta):
grad = np.zeros(theta.shape)
error = (model(X, theta)- y).ravel()
for j in range(len(theta.ravel())): #for each parmeter
term = np.multiply(error, X[:,j])
grad[0, j] = np.sum(term) / len(X)
return grad梯度下降停止策略
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
def stopCriterion(type, value, threshold):
# 设定三种不同的停止策略
if type == STOP_ITER: # 设定迭代次数
return value > threshold
elif type == STOP_COST: # 根据损失值停止
return abs(value[-1] - value[-2]) < threshold
elif type == STOP_GRAD: # 根据梯度变化停止
return np.linalg.norm(value) < threshold样本重新洗牌
import numpy.random
#洗牌
def shuffleData(data):
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols-1]
y = data[:, cols-1:]
return X, y梯度下降求解
def descent(data, theta, batchSize, stopType, thresh, alpha):
# 梯度下降求解
init_time = time.time()
i = 0 # 迭代次数
k = 0 # batch
X, y = shuffleData(data)
grad = np.zeros(theta.shape) # 计算的梯度
costs = [cost(X, y, theta)] # 损失值
while True:
grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
k += batchSize # 取batch数量个数据
if k >= n:
k = 0
X, y = shuffleData(data) # 重新洗牌
theta = theta - alpha * grad # 参数更新
costs.append(cost(X, y, theta)) # 计算新的损失
i += 1
if stopType == STOP_ITER:
value = i
elif stopType == STOP_COST:
value = costs
elif stopType == STOP_GRAD:
value = grad
if stopCriterion(stopType, value, thresh): break
return theta, i - 1, costs, grad, time.time() - init_time完整代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import numpy.random
import time
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def model(X, theta):
return sigmoid(np.dot(X, theta.T))
def cost(X, y, theta):
left = np.multiply(-y, np.log(model(X, theta)))
right = np.multiply(1 - y, np.log(1 - model(X, theta)))
return np.sum(left - right) / (len(X))
def gradient(X, y, theta):
grad = np.zeros(theta.shape)
error = (model(X, theta) - y).ravel()
for j in range(len(theta.ravel())): # for each parmeter
term = np.multiply(error, X[:, j])
grad[0, j] = np.sum(term) / len(X)
return grad
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
def stopCriterion(type, value, threshold):
# 设定三种不同的停止策略
if type == STOP_ITER: # 设定迭代次数
return value > threshold
elif type == STOP_COST: # 根据损失值停止
return abs(value[-1] - value[-2]) < threshold
elif type == STOP_GRAD: # 根据梯度变化停止
return np.linalg.norm(value) < threshold
# 洗牌
def shuffleData(data):
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols - 1]
y = data[:, cols - 1:]
return X, y
def descent(data, theta, batchSize, stopType, thresh, alpha):
# 梯度下降求解
init_time = time.time()
i = 0 # 迭代次数
k = 0 # batch
X, y = shuffleData(data)
grad = np.zeros(theta.shape) # 计算的梯度
costs = [cost(X, y, theta)] # 损失值
while True:
grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
k += batchSize # 取batch数量个数据
if k >= n:
k = 0
X, y = shuffleData(data) # 重新洗牌
theta = theta - alpha * grad # 参数更新
costs.append(cost(X, y, theta)) # 计算新的损失
i += 1
if stopType == STOP_ITER:
value = i
elif stopType == STOP_COST:
value = costs
elif stopType == STOP_GRAD:
value = grad
if stopCriterion(stopType, value, thresh): break
return theta, i - 1, costs, grad, time.time() - init_time
def runExpe(data, theta, batchSize, stopType, thresh, alpha):
# import pdb
# pdb.set_trace()
theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)
name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled"
name += " data - learning rate: {} - ".format(alpha)
if batchSize == n:
strDescType = "Gradient" # 批量梯度下降
elif batchSize == 1:
strDescType = "Stochastic" # 随机梯度下降
else:
strDescType = "Mini-batch ({})".format(batchSize) # 小批量梯度下降
name += strDescType + " descent - Stop: "
if stopType == STOP_ITER:
strStop = "{} iterations".format(thresh)
elif stopType == STOP_COST:
strStop = "costs change < {}".format(thresh)
else:
strStop = "gradient norm < {}".format(thresh)
name += strStop
print("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
name, theta, iter, costs[-1], dur))
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(np.arange(len(costs)), costs, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title(name.upper() + ' - Error vs. Iteration')
return theta
path = 'data' + os.sep + 'LogiReg_data.txt'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
# 画图观察样本情况
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
pdData.insert(0, 'Ones', 1)
# 划分训练数据与标签
orig_data = pdData.values
cols = orig_data.shape[1]
X = orig_data[:, 0:cols - 1]
y = orig_data[:, cols - 1:cols]
# 设置初始参数0
theta = np.zeros([1, 3])
# 选择的梯度下降方法是基于所有样本的
n = 100
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)
runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)
from sklearn import preprocessing as pp
# 数据预处理
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)
theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002 / 5, alpha=0.001)
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002 * 2, alpha=0.001)
# 设定阈值
def predict(X, theta):
return [1 if x >= 0.5 else 0 for x in model(X, theta)]
# 计算精度
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))逻辑回归的优缺点
优点
形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大。
模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差,并且特征工程可以大家并行开发,大大加快开发的速度。
训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
资源占用小,尤其是内存。因为只需要存储各个维度的特征值。
方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)。
缺点
准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。
处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。
逻辑回归本身无法筛选特征。有时候,我们会用gbdt来筛选特征,然后再上逻辑回归。
以上是python如何实现梯度下降求解逻辑回归的详细内容。更多信息请关注PHP中文网其他相关文章!
 Python与C:学习曲线和易用性Apr 19, 2025 am 12:20 AM
Python与C:学习曲线和易用性Apr 19, 2025 am 12:20 AMPython更易学且易用,C 则更强大但复杂。1.Python语法简洁,适合初学者,动态类型和自动内存管理使其易用,但可能导致运行时错误。2.C 提供低级控制和高级特性,适合高性能应用,但学习门槛高,需手动管理内存和类型安全。
 Python vs. C:内存管理和控制Apr 19, 2025 am 12:17 AM
Python vs. C:内存管理和控制Apr 19, 2025 am 12:17 AMPython和C 在内存管理和控制方面的差异显着。 1.Python使用自动内存管理,基于引用计数和垃圾回收,简化了程序员的工作。 2.C 则要求手动管理内存,提供更多控制权但增加了复杂性和出错风险。选择哪种语言应基于项目需求和团队技术栈。
 科学计算的Python:详细的外观Apr 19, 2025 am 12:15 AM
科学计算的Python:详细的外观Apr 19, 2025 am 12:15 AMPython在科学计算中的应用包括数据分析、机器学习、数值模拟和可视化。1.Numpy提供高效的多维数组和数学函数。2.SciPy扩展Numpy功能,提供优化和线性代数工具。3.Pandas用于数据处理和分析。4.Matplotlib用于生成各种图表和可视化结果。
 Python和C:找到合适的工具Apr 19, 2025 am 12:04 AM
Python和C:找到合适的工具Apr 19, 2025 am 12:04 AM选择Python还是C 取决于项目需求:1)Python适合快速开发、数据科学和脚本编写,因其简洁语法和丰富库;2)C 适用于需要高性能和底层控制的场景,如系统编程和游戏开发,因其编译型和手动内存管理。
 数据科学和机器学习的PythonApr 19, 2025 am 12:02 AM
数据科学和机器学习的PythonApr 19, 2025 am 12:02 AMPython在数据科学和机器学习中的应用广泛,主要依赖于其简洁性和强大的库生态系统。1)Pandas用于数据处理和分析,2)Numpy提供高效的数值计算,3)Scikit-learn用于机器学习模型构建和优化,这些库让Python成为数据科学和机器学习的理想工具。
 学习Python:2小时的每日学习是否足够?Apr 18, 2025 am 12:22 AM
学习Python:2小时的每日学习是否足够?Apr 18, 2025 am 12:22 AM每天学习Python两个小时是否足够?这取决于你的目标和学习方法。1)制定清晰的学习计划,2)选择合适的学习资源和方法,3)动手实践和复习巩固,可以在这段时间内逐步掌握Python的基本知识和高级功能。
 Web开发的Python:关键应用程序Apr 18, 2025 am 12:20 AM
Web开发的Python:关键应用程序Apr 18, 2025 am 12:20 AMPython在Web开发中的关键应用包括使用Django和Flask框架、API开发、数据分析与可视化、机器学习与AI、以及性能优化。1.Django和Flask框架:Django适合快速开发复杂应用,Flask适用于小型或高度自定义项目。2.API开发:使用Flask或DjangoRESTFramework构建RESTfulAPI。3.数据分析与可视化:利用Python处理数据并通过Web界面展示。4.机器学习与AI:Python用于构建智能Web应用。5.性能优化:通过异步编程、缓存和代码优
 Python vs.C:探索性能和效率Apr 18, 2025 am 12:20 AM
Python vs.C:探索性能和效率Apr 18, 2025 am 12:20 AMPython在开发效率上优于C ,但C 在执行性能上更高。1.Python的简洁语法和丰富库提高开发效率。2.C 的编译型特性和硬件控制提升执行性能。选择时需根据项目需求权衡开发速度与执行效率。


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

WebStorm Mac版
好用的JavaScript开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

SublimeText3 Linux新版
SublimeText3 Linux最新版

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。




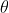 的函数
的函数

