Java怎么实现优先队列式广度优先搜索算法

1.问题描述

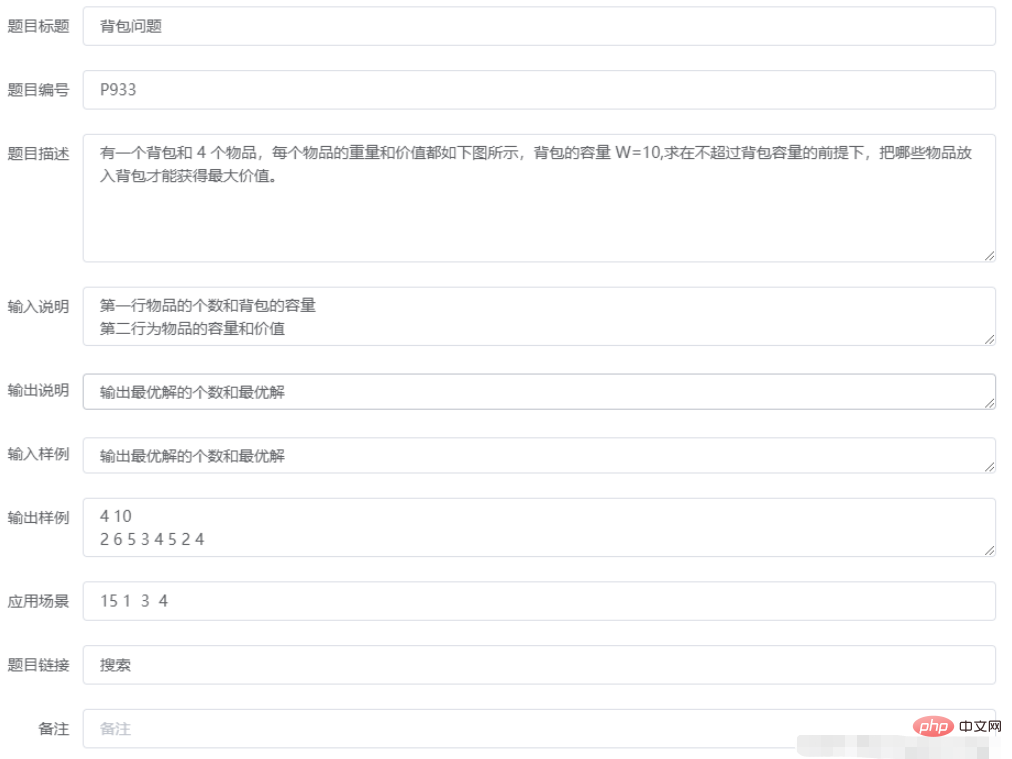
2.实现

package com.platform.modules.alg.alglib.p933;
 
import java.util.Arrays;
import java.util.PriorityQueue;
 
public class P933 {
    public static final int N = 10;
    // 记录最优解
    boolean bestx[] = new boolean[N];
    // 辅助数组,用于存储排序后的重量和价值
    private int w[] = new int[N];
    private int v[] = new int[N];
    Goods goods[] = new Goods[N];
    Object S[] = new Object[N];
    // 用来记录最优解
    Integer bestp;
    // 为背包的最大容量
    int W;
    // 为物品的个数。
    int n;
    // 为所有物品的总重量。
    int sumw;
    // 为所有物品的总价值
    int sumv;
    public String output = "";
 
    public P933() {
        for (int i = 0; i < goods.length; i++) {
            goods[i] = new Goods();
        }
        for (int i = 0; i < S.length; i++) {
            S[i] = new Object();
        }
    }
 
    // 计算节点的上界
    double Bound(Node tnode) {
        // 已装入背包物品价值
        double maxvalue = tnode.cp;
        int t = tnode.id; // 排序后序号
        double left = tnode.rw; // 剩余容量
        while (t <= n && w[t] <= left) {
            maxvalue += v[t];
            left -= w[t++];
        }
        if (t <= n)
            maxvalue += ((double) (v[t])) / w[t] * left;
        return maxvalue;
    }
 
    public String cal(String input) {
 
 
        String[] line = input.split("\n");
        String[] words = line[0].split(" ");
        // 物品的个数和背包的容量
        n = Integer.parseInt(words[0]);
        W = Integer.parseInt(words[1]);
        bestp = 0; // 用来记录最优解
        sumw = 0; // sumw 为所有物品的总重量。
        sumv = 0; // sumv为所有物品的总价值
 
        words = line[1].split(" ");
        for (int i = 1; i <= words.length / 2; i++) { // 输入每个物品的重量和价值,用空格分开
            goods[i].weight = Integer.parseInt(words[2 * i - 2]);
            goods[i].value = Integer.parseInt(words[2 * i - 1]);
            sumw += goods[i].weight;
            sumv += goods[i].value;
            S[i - 1].id = i;
            S[i - 1].d = 1.0 * goods[i].value / goods[i].weight;
        }
        if (sumw <= W) {
            bestp = sumv;
            output = bestp.toString();
            return output;
        }
        Arrays.sort(S); // 按价值重量比非递增排序
        for (int i = 1; i <= n; i++) {//把排序后的数据传递给辅助数组
            w[i] = goods[S[i - 1].id].weight;
            v[i] = goods[S[i - 1].id].value;
        }
        priorbfs();//优先队列分支限界法
        output += bestp + "\n";
 
        for (int i = 1; i <= n; i++) { // 输出最优解
            if (bestx[i])
                output += S[i - 1].id + " "; // 输出原物品序号(排序前的)
        }
        return output;
    }
 
    // 优先队列式分支限界法
    int priorbfs() {
        // 当前处理的物品序号t，当前装入背包物品价值tcp,当前剩余容量trw
        int t, tcp, trw;
        double tup;  // 当前价值上界 tup
        PriorityQueue<Node> q = new PriorityQueue<>(); // 优先队列
 
        q.add(new Node(0, sumv, W, 1)); // 初始化,根结点加入优先队列
        while (!q.isEmpty()) {
            // 定义三个结点型变量
            Node livenode;
            Node lchild = new Node();
            Node rchild = new Node();
            livenode = q.peek(); // 取出队头元素作为当前扩展结点 livenode
            q.poll(); // 队头元素出队
            t = livenode.id; // 当前处理的物品序号
            // 搜到最后一个物品的时候不需要往下搜索。
            // 如果当前的背包没有剩余容量(已经装满)了，不再扩展。
            if (t > n || livenode.rw == 0) {
                if (livenode.cp >= bestp) { // 更新最优解和最优值
                    for (int i = 1; i <= n; i++)
                        bestx[i] = livenode.x[i];
                    bestp = livenode.cp;
                }
                continue;
            }
            if (livenode.up < bestp)//如果不满足不再扩展
                continue;
            tcp = livenode.cp; //当前背包中的价值
            trw = livenode.rw; //背包剩余容量
            if (trw >= w[t]) { //扩展左孩子，满足约束条件，可以放入背包
                lchild.cp = tcp + v[t];
                lchild.rw = trw - w[t];
                lchild.id = t + 1;
                tup = Bound(lchild); //计算左孩子上界
                lchild = new Node(lchild.cp, tup, lchild.rw, lchild.id);
                for (int i = 1; i <= n; i++)//复制以前的解向量
                    lchild.x[i] = livenode.x[i];
                lchild.x[t] = true;
                if (lchild.cp > bestp)//比最优值大才更新
                    bestp = lchild.cp;
                q.add(lchild);//左孩子入队
            }
            rchild.cp = tcp;
            rchild.rw = trw;
            rchild.id = t + 1;
            tup = Bound(rchild);//计算右孩子上界
            if (tup >= bestp) {//扩展右孩子，满足限界条件，不放入
                rchild = new Node(tcp, tup, trw, t + 1);
                for (int i = 1; i <= n; i++)//复制以前的解向量
                    rchild.x[i] = livenode.x[i];
                rchild.x[t] = false;
                q.add(rchild);//右孩子入队
            }
        }
        return bestp;//返回最优值。
    }
}
 
// 定义结点。每个节点来记录当前的解。
class Node implements Comparable<Node> {
    int cp; // cp 为当前装入背包的物品总价值
    double up; // 价值上界
    int rw; //  剩余容量
    int id; // 物品号
    boolean x[] = new boolean[P933.N]; // 解向量
 
    Node() {
    }
 
    Node(int _cp, double _up, int _rw, int _id) {
        cp = _cp;
        up = _up;
        rw = _rw;
        id = _id;
    }
 
    @Override
    public int compareTo(Node o) {
        return (this.up - o.up) > 0 ? 1 : -1;
    }
}
 
// 物品
class Goods {
    int weight; // 重量
    int value; // 价值
}
 
// 辅助物品结构体，用于按单位重量价值(价值/重量比)排序
class Object implements Comparable {
    int id; // 序号
    double d; // 单位重量价值
 
 
    @Override
    public int compareTo(java.lang.Object o) {
        return this.d > ((Object) o).d ? -1 : 1;
    }
}

3.测试

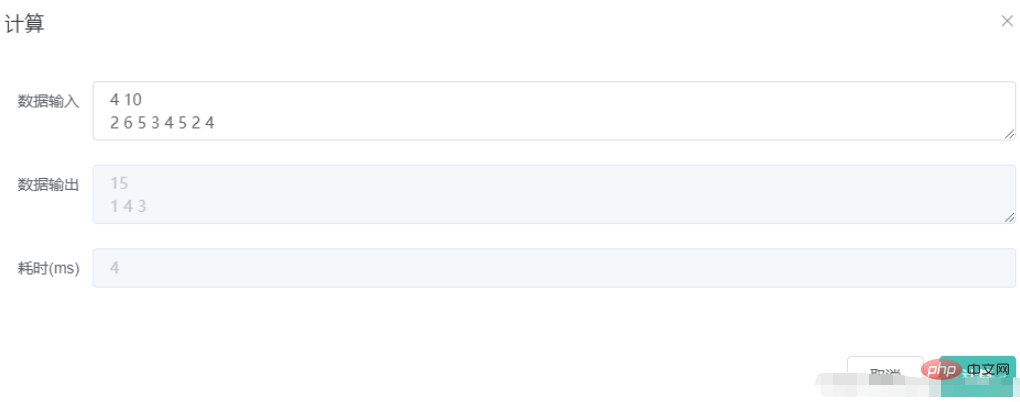
以上是Java怎么实现优先队列式广度优先搜索算法的详细内容。更多信息请关注PHP中文网其他相关文章！