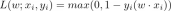数学推理是人类智能的关键体现,它使我们能够理解并做出基于数值数据和语言的决策。数学推理适用于各个领域,包括科学、工程、金融和日常生活,并包含一系列能力,诸如从模式识别、数字运算等基本技能到解决问题、逻辑推理和抽象思维等高级技能。
长期以来,开发能够解决数学问题、证明数学定理的 AI 系统是机器学习和自然语言处理领域的研究重点。这也可以追溯到 20 世纪 60 年代。
在深度学习兴起的近十年,人们对这一领域的兴趣更是大幅增长:
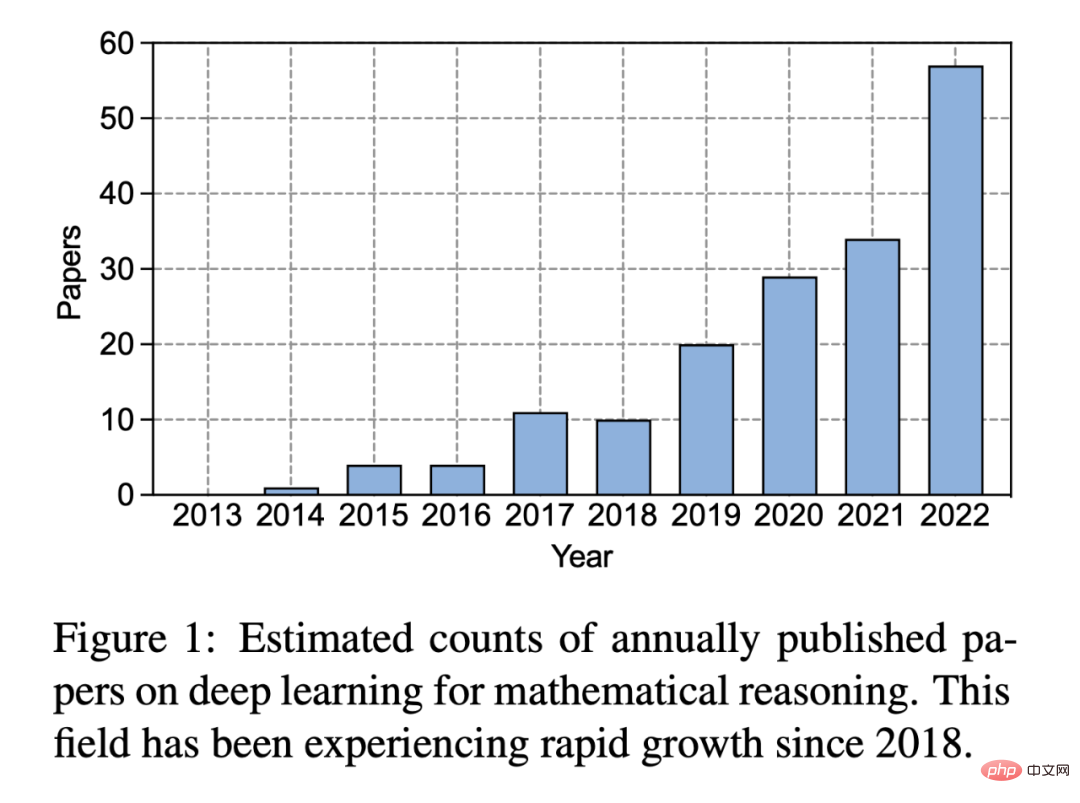
图 1:每年发表的关于数学推理的深度学习论文的预估数量。自 2018 年以来,这一领域经历了快速增长。
深度学习在各种自然语言处理任务中显示出巨大的成功,如问题回答和机器翻译。同样,研究人员开发了各种用于数学推理的神经网络方法,这些方法在处理应用题、定理证明和几何问题解决等复杂任务时已被证明是有效的。例如,基于深度学习的应用题求解器采用了一个序列到序列的框架,并以注意力机制作为中间步骤生成数学表达式。此外,通过大规模语料库和 Transformer 模型,预训练的语言模型在各种数学任务上取得了可喜的成果。最近,像 GPT-3 这样的大型语言模型在复杂推理和语境学习中表现出令人印象深刻的能力,进一步推动了数学推理领域的发展。
在近期发布的一篇报告中,来自 UCLA 等机构的研究者系统回顾了深度学习在数学推理方面的进展。

论文链接:https://arxiv.org/pdf/2212.10535.pdf
项目地址:https://github.com/lupantech/dl4math
具体而言,本文讨论了各种任务和数据集(第 2 节),并研究了神经网络(第 3 节)和预训练语言模型(第 4 节)在数学领域的进展。此外还探讨了大型语言模型的上下文学习在数学推理中的快速发展(第 5 节)。文章进一步分析了现有的基准,发现对多模态和低资源环境的关注较少(第 6.1 节)。基于循证的研究表明,目前的计算能力表征是不充分的,深度学习方法在数学推理方面也是不一致的(第 6.2 节)。随后,作者建议在概括性和鲁棒性、可信推理、从反馈中学习和多模态数学推理方面改进目前的工作(第 7 节)。
任务和数据集
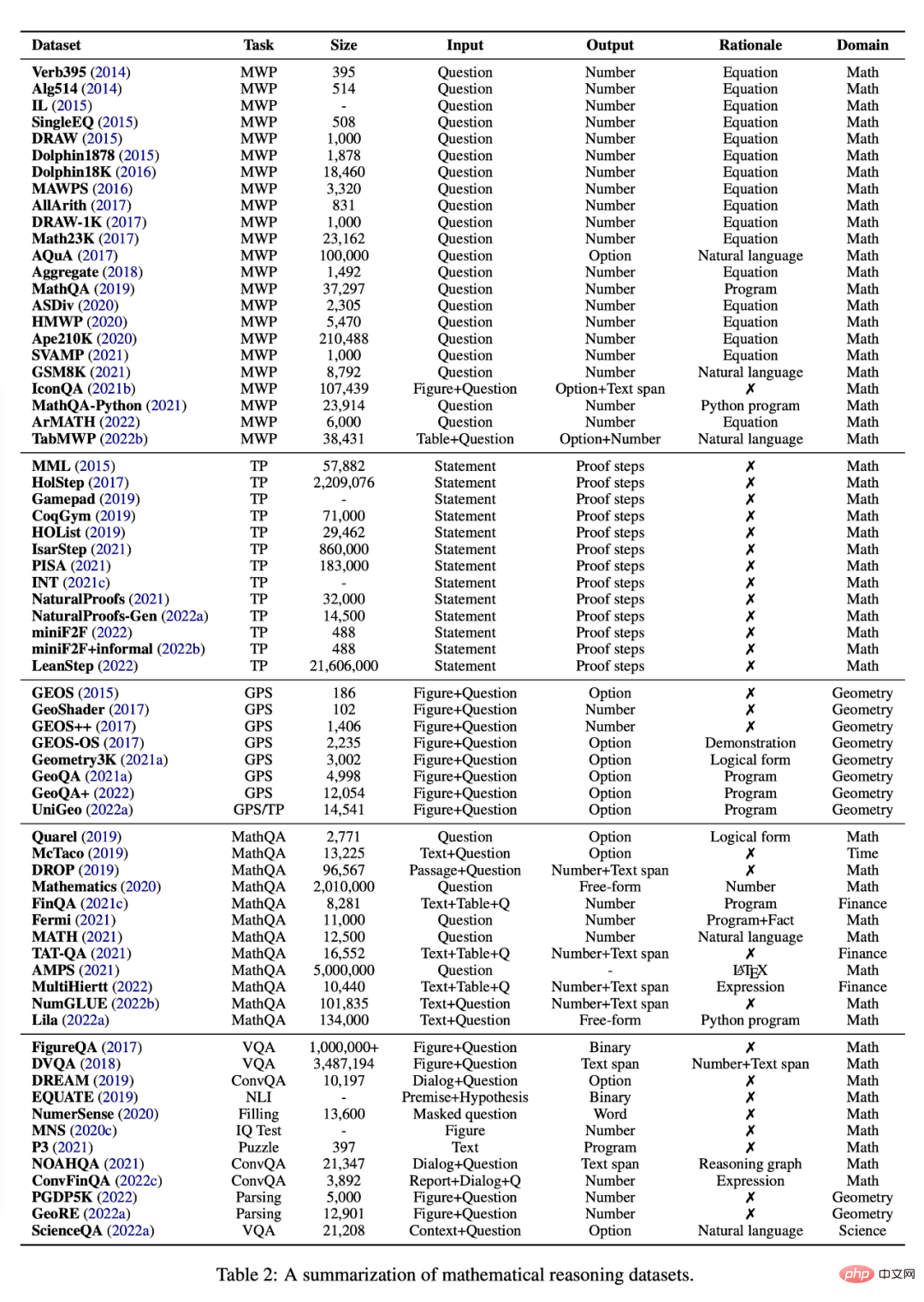
本节研究了目前可用于研究使用深度学习方法的数学推理的各种任务和数据集,见表 2。
应用题 (Math Word Problem)
应用题包含一个涉及人物、实体和数量的简短叙述其,数学关系可以用一组方程来模拟,方程的解揭示了问题的最终答案。表 1 就是一个典型的例子。一个问题涉及加、减、乘、除四种基本的数学运算,有单一或多个运算步骤。应用题对 NLP 系统的挑战在于对语言理解、语义解析和多种数学推理能力的需求。

现有的应用题数据集涵盖了小学阶段的问题,这些问题是从在线学习网站上抓取的、从教科书中收集的或由人类手动注释的。早期的应用题数据集相对较小,或者仅限于少量的操作步骤。最近的一些数据集旨在增加问题的多样性和难度。例如,目前最大的公开问题集 Ape210K 由 210k 个小学应用题组成;而 GSM8K 中的问题可以涉及多达 8 个步骤的解法。SVAMP 是一个基准,测试深度学习模型对具有简单变化的应用题的鲁棒性。一些最近建立的数据集还涉及文本以外的模态。例如,IconQA 提供了一个抽象的图表作为视觉背景,而 TabMWP 为每个问题提供了一个表格形式的背景。
大多数应用题数据集会提供注释方程作为解决方案的理由(如表 1)。为了提高学习的求解器的性能和可解释性,MathQA 用精确的运算程序进行注释,MathQA-Python 则提供具体的 Python 程序。另一些数据集用多步骤的自然语言解决方案对问题进行注释,这些解决方案被认为更适合人类阅读。Lila 用 Python 程序的原理注释了许多前面提到的应用题数据集。
理论证明
定理证明自动化是 AI 领域的一个长期挑战。问题通常是通过一连串的逻辑论证来证明一个数学定理的真理性。定理证明涉及各种技能,如选择高效的多步骤策略、使用背景知识以及进行符号运算(如算术或推导)。
最近,人们对在形式化的交互式定理证明器(ITP)中使用语言模型进行定理证明越来越感兴趣。定理会在 ITP 的编程语言中被陈述,然后通过生成「证明步骤」来简化,直到它被简化为已知事实。其结果是一个步骤序列,构成一个验证的证明。
非形式化定理证明提出了定理证明的另一种媒介,即用自然语言和「标准」数学符号(如 LATEX)的混合形式来编写语句和证明,并由人类检查其正确性。
一个新兴的研究领域旨在结合非正式和正式定理证明的要素。例如,Wu et al. (2022b) 探索将非形式化语句翻译成形式化语句,而 Jiang et al. (2022b)发布了一个新版本的 miniF2F 基准,其中增加了非形式化语句和证明,称为 miniF2F+informal。Jiang et al. (2022b)探索将提供(或生成)的非形式化证明转化为形式化证明。
几何问题
几何问题自动化求解(GPS)也是数学推理研究中一个长期存在的人工智能任务,并在近年来引起了广泛关注。与应用题不同,几何问题由自然语言的文本描述和几何图形组成。如图 2 所示,多模态输入描述了几何元素的实体、属性和关系,而目标是找到未知变量的数值解。由于需要复杂的技能,GPS 对深度学习方法来说是一项具有挑战性的任务。它涉及到解析多模态信息、进行符号抽象、利用定理知识和进行定量推理的能力。
早期的数据集促进了这一领域的研究,然而这些数据集相对较小或不公开,这限制了深度学习方法的发展。为了应对这一限制,Lu et al. 创建了 Geometry3K 数据集,该数据集由 3002 个多选几何问题组成,并对多模态输入进行了统一的逻辑形式注释。最近,更大规模的数据集,如 GeoQA、GeoQA + 和 UniGeo 已经被引入,并被注释了可以被神经求解器学习并执行以获得最终答案的程序。
数学问答
最近的研究表明,SOTA 数学推理系统在推理上可能存在「脆性」,即模型依靠特定数据集的虚假信号和即插即用的计算来达到「令人满意」的性能。为了解决这个问题,人们从各个方面提出了新的基准。The Mathematics (Saxton et al., 2020) 数据集包括许多不同类型的数学问题,涵盖算术、代数、概率和微积分。该数据集可以测量模型的代数泛化能力。同样,MATH (Hendrycks et al., 2021) 由具有挑战性的竞赛数学组成,以衡量模型在复杂情况下的问题解决能力。
一些工作在问题输入中加入了表格背景。例如,FinQA、TAT-QA 和 MultiHiertt 收集了需要表格理解和数值推理来回答的问题。一些研究则提出了大规模的数值推理的统一基准。NumGLUE (Mishra et al., 2022b) 是一个多任务基准,目标是评估模型在八个不同任务上的表现。Mishra et al. 2022a 提出了 Lila,进一步推动了这一方向,Lila 由 23 个数值推理任务组成,跨越了广泛的数学主题、语言复杂性、问题格式和背景知识要求。
AI 同样在其他类型的定量问题上有所成就。比如数字、图表和绘图,是以简明的方式传达大量信息的基本媒介。FigureQA、DVQA、MNS、PGDP5K 和 GeoRE 都是为了研究模型对基于图表的实体间的定量关系进行推理的能力推出的。NumerSense 研究了现有的预训练语言模型是否以及在多大程度上能够感应数值常识知识。EQUATE 在自然语言推理框架中对定量推理的各个方面进行了形式化。定量推理还经常出现在金融、科学和编程等特定领域。例如,ConvFinQA 以对话式问答的形式对财务报告进行数字推理;ScienceQA 涉及科学领域的数字推理;而 P3 研究了深度学习模型的函数推理能力,找到一个有效的输入让给定的程序返回 True。
用于数学推理的神经网络
对于常见的用于数学推理的几种神经网络,本文的作者也进行了总结。
Seq2Seq 网络
Seq2Seq 神经网络已经成功地应用于数学推理任务,如应用题、定理证明、几何问题和数学问题回答。Seq2Seq 模型使用编码器 - 解码器架构,通常将数学推理形式化为一个序列生成任务。这种方法的基本思想是将输入序列(如数学问题)映射到输出序列(如方程式、程序和证明)。常见的编码器和解码器包括长短时记忆网络(LSTM)、门控递归单元(GRU)。大量的工作表明,Seq2Seq 模型比以前的统计学习方法具有性能优势,包括它们的双向变体 BiLSTM 和 BiGRU。DNS 是第一项使用 Seq2Seq 模型将应用题中的句子转化为数学方程的工作。
基于图的网络
Seq2Seq 方法具备生成数学表达式和不依赖手工制作特征的优势。数学表达式可以转化为基于树的结构,例如抽象语法树(AST)和基于图的结构,描述了表达式中的结构化信息。然而,这种重要的信息并没有被 Seq2Seq 方法明确地建模。为了解决这个问题,研究者开发了基于图的神经网络来明确地模拟表达式中的结构。
Sequence-to-tree(Seq2Tree)模型在对输出序列进行编码时明确地对树结构进行建模。例如,Liu et al. 设计了一个 Seq2Tree 模型来更好地利用方程的 AST 信息。相反,Seq2DAG 在生成方程时应用了一个序列图(Seq2Graph)框架,因为图解码器能够提取多个变量之间的复杂关系。在对输入的数学序列进行编码时,也可以嵌入基于图的信息。例如,ASTactic 在 AST 上应用 TreeLSTM 来表示定理证明的输入目标和前提。
基于注意力的网络
注意力机制已成功应用于自然语言处理和计算机视觉问题,在解码处理过程中考虑到了输入的隐藏矢量。研究人员一直在探索它在数学推理任务中的作用,因为它可以用来识别数学概念之间最重要的关系。例如,MATH-EN 是一个应用题求解器,它得益于通过自注意力学习的长距离依赖信息。基于注意力的方法也被应用于其他数学推理任务,如几何问题和定理证明。为了提取更好的表征,人们研究了各种注意力机制,如使用不同的多头注意力来提取各种类型的 MWP 特征的 Group-ATT,以及被应用于提取 knowledge-aware 信息的图注意力。
其他神经网络
数学推理任务的深度学习方法也可以利用其他神经网络,如卷积神经网络和多模态网络。一些工作使用卷积神经网络架构对输入文本进行编码,使模型有能力捕捉输入中符号之间的长期关系。例如,Irving et al. 研究提出了深度神经网络在定理证明中的第一个应用,它依靠卷积网络在大型理论中进行前提选择。
多模态数学推理任务,如几何问题解决和基于图表的数学推理,被形式化为视觉问题答案(VQA)问题。在这个领域,视觉输入使用 ResNet 或 Faster-RCNN 进行编码,而文本表征则通过 GRU 或 LTSM 获得。随后,使用多模态融合模型学习联合表征,如 BAN、FiLM 和 DAFA。
其他深度神经网络结构也可用于数学推理。Zhang et al. 利用图谱神经网络(GNN)在空间推理中的成功,将其用于几何问题。由于能够解决纵向时间序列数据,WaveNet 被应用于定理证明。此外,在 DDT 中生成数学方程方面,Transformer 被发现优于 GRU。以及,MathDQN 是第一个探索解决数学应用题的强化学习工作,主要利用其强大的搜索能力。
用于数学推理的预训练语言模型
预训练的语言模型已经在广泛的 NLP 任务上表现出显著的性能提升,同样应用于数学相关的问题,此前的工作表明,预训练语言模型在解答应用题上有很好的表现,协助进行定理证明以及其他数学任务。然而,将其用于数学推理却存在若干挑战。
首先,预训练语言模型不是专门针对数学数据的训练。这可能导致它们在数学相关任务中的熟练程度低于自然语言任务。与文本数据相比,可用于大规模预训练的数学或科学数据也较少。
其次,预训练模型的规模持续增长,使得为特定的下游任务从头开始训练整个模型的成本很高。
此外,下游任务可能会处理不同的输入格式或模态,如结构化表格或图表。为了应对这些挑战,研究者必须通过在下游任务上对预训练模型进行微调或调整神经架构。
最后,尽管预训练的语言模型可以编码大量的语言信息,但仅从语言建模的目标来看,模型可能很难学习数字表示或高级推理技能。考虑到这一点,最近有研究调查了从基础知识开始的课程对数学相关技能的注入。
数学的自监督学习
下表 4 提供了一个预训练了数学推理的自监督任务的语言模型列表。
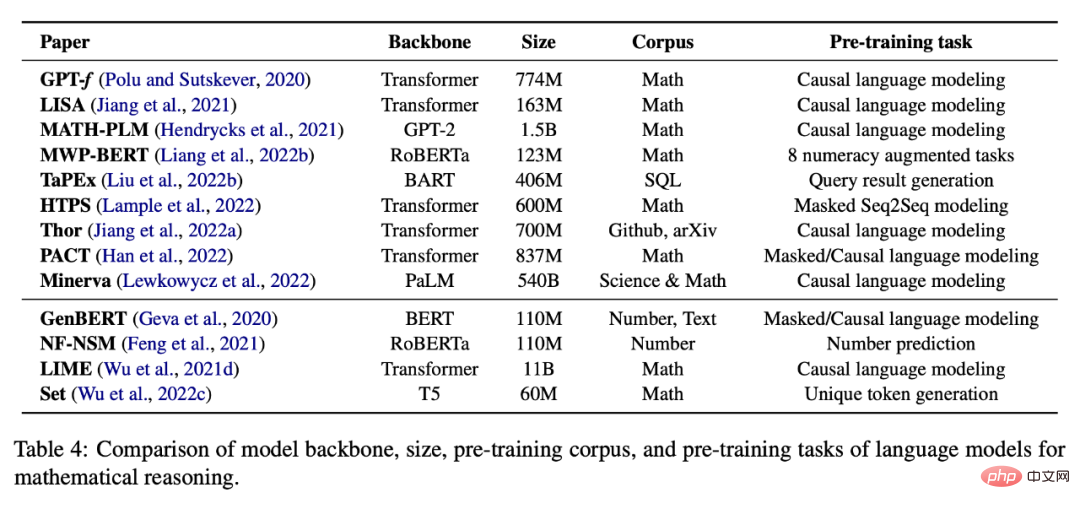
特定任务的数学微调
当没有足够的数据来从头训练大型模型时,特定任务的微调也是一种常见的做法。如表 5 所示,现有的工作尝试了在各种下游任务上对预训练语言模型进行微调。
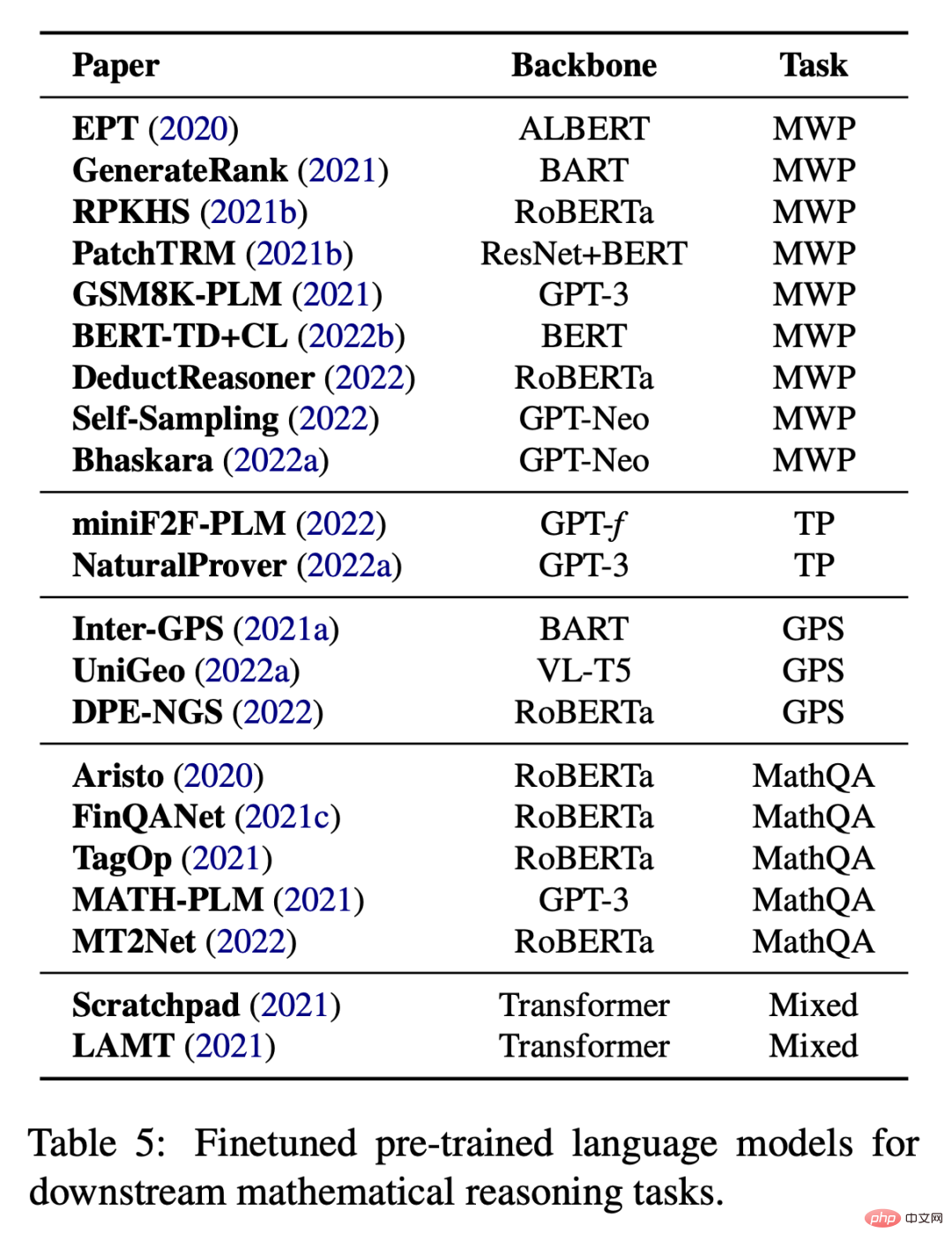
除了对模型参数进行微调,很多工作还使用预训练语言模型作为编码器,将其与其他模块组合起来完成下游任务,例如,IconQA 提出将 ResNet 和 BERT 分别用于图表识别和文本理解。
数学推理中的上下文学习
一个上下文的样本通常包含一个输入 - 输出对和一些 prompt 词,例如,请从列表中选择最大的数字。
输入:[2, 4, 1, 5, 8]
输出:8。
少样本学习会给出多个样本,然后模型在最后一个输入样本时预测输出。然而这种标准的少样本 prompting,即在 test-time 样本前给大型语言模型提供输入 - 输出对的上下文样本,还没有被证明足以在数学推理等挑战性任务上取得良好表现。
思维链(Chain-of-thought prompting,CoT)利用中间的自然语言解释作为 prompt,使大型语言模型首先生成推理链,然后预测一个输入问题的答案。例如,一个解决应用题的 CoT prompt 可以是

Kojima et al.(2022)提出,为模型提供「让我们一步一步地思考!(Let’s think step by step!)」的 prompt 会让大型语言模型成为良好的零样本推理器。除此之外,近期的大部分工作都集中在如何在零样本推理的设置下改进思维链推理。这类工作主要分为两部分:(i)选择更好的上下文样本和(ii)创造更好的推理链。
上下文样本选择
早期的思维链工作是随机地或启发式地选择上下文样本。最近的研究却表明,在不同的上下文例子选择中,这种类型的少样本学习可能是非常不稳定的。因此,哪些上下文的推理样本能做出最高效的 prompt,在学术上仍是一个未知的问题。
为了解决这个局限,最近的一些工作研究了各种方法来优化上下文样本的选择过程。例如,Rubin et al.(2022)试图通过检索语义相似的样本来解决这个问题。然而,这种方法在数学推理问题上效果不佳,而且如果包含结构化信息(如表格)就很难衡量相似性。此外,Fu et al.(2022)提出了基于复杂性的 prompt,选择具有复杂推理链的样本(即具有更多推理步骤的链)作为 prompt。Lu et al.(2022b)提出了一种通过强化学习来选择上下文样本的方法。具体来说,智能体学习从候选池中找到最佳的上下文样本,目的是在与 GPT-3 环境互动时,使给定的训练样本的预测奖励最大化。此外,Zhang et al.(2022b)发现示例问题的多样化也可以提高模型性能。他们提出了一个两步法来构建上下文中的示例问题:首先,将给定数据集的问题划分为几个群组;其次,从每个群组中选择一个有代表性的问题,并使用具有简单启发式的零样本思维链生成其推理链。
高质量推理链
早期的思维链工作主要依靠单一的人类注释推理链作为 prompt。然而,人工创建推理链有两个缺点:首先,随着任务变得越来越复杂,目前的模型可能不足以学会执行所有必要的推理步骤,而且不能轻易推广到不同的任务;其次,单一的解码过程很容易受到错误推理步骤的影响,导致最终的答案是不正确的预测。为了解决这个限制,最近的研究主要集中在两个方面:(i)手工制作更复杂的示例,称为基于过程的方法;(ii)利用类似集合的方法,称为基于结果的方法。
在评估现有的基准和方法之后,作者还讨论了这一领域的未来研究方向。更多研究细节,可参考原论文。
以上是十年来论文量激增,深度学习如何慢慢推开数学推理的门的详细内容。更多信息请关注PHP中文网其他相关文章!
 优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM
优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM介绍 恭喜!您经营一家成功的业务。通过您的网页,社交媒体活动,网络研讨会,会议,免费资源和其他来源,您每天收集5000个电子邮件ID。下一个明显的步骤是
 Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM
Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM介绍 在当今快节奏的软件开发环境中,确保最佳应用程序性能至关重要。监视实时指标,例如响应时间,错误率和资源利用率可以帮助MAIN
 Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM“您有几个用户?”他扮演。 阿尔特曼回答说:“我认为我们上次说的是每周5亿个活跃者,而且它正在迅速增长。” “你告诉我,就像在短短几周内翻了一番,”安德森继续说道。 “我说那个私人
 pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介绍 Mistral发布了其第一个多模式模型,即Pixtral-12b-2409。该模型建立在Mistral的120亿参数Nemo 12B之上。是什么设置了该模型?现在可以拍摄图像和Tex
 生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
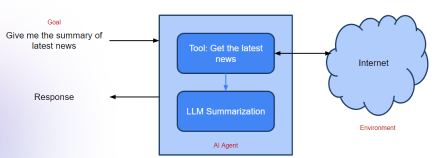
生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想象一下,拥有一个由AI驱动的助手,不仅可以响应您的查询,还可以自主收集信息,执行任务甚至处理多种类型的数据(TEXT,图像和代码)。听起来有未来派?在这个a


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

SublimeText3 Linux新版
SublimeText3 Linux最新版

EditPlus 中文破解版
体积小,语法高亮,不支持代码提示功能

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

记事本++7.3.1
好用且免费的代码编辑器