译者 | 赵青窕
审校 | 孙淑娟
前言
在机器学习中,分类具有两个阶段,分别是学习阶段和预测阶段。在学习阶段,基于给定的训练数据建立模型;在预测阶段,该模型用于预测给定数据的响应。决策树是最容易理解和解释的分类算法之一。
在机器学习中,分类具有两个阶段,分别是学习阶段和预测阶段。在学习阶段,基于给定的训练数据建立模型;在预测阶段,该模型用于预测给定数据的响应。决策树是最容易理解和解释的分类算法之一。
决策树算法
决策树算法属于监督学习算法中的一种。与其他监督学习算法不同,决策树算法可以用于解决回归和分类问题。
使用决策树的目的是创建一个训练模型,通过学习从之前的数据(训练数据)推断出的简单决策规则来预测目标变量的类或值。
在决策树中,我们从树的根开始来预测一个记录的类标签。我们将根属性的值与记录的属性进行比较,在比较的基础上,我们跟随该值对应的分支并跳转到下一个节点。
决策树的类型
基于我们所拥有的目标变量的类型,我们可以把树分为两种类型:
1.分类变量决策树:有一个分类目标变量的决策树,称为分类变量决策树。
2.连续变量决策树:决策树的目标变量是连续的,因此称为连续变量决策树。
例子:假设我们有一个预测客户是否会向保险公司支付续期保费的问题。这里客户的收入是一个重要的变量,但保险公司没有所有客户的收入细节。现在,我们知道这是一个重要的变量,然后我们可以建立一个决策树,基于职业,产品和其他各种变量来预测客户的收入。在这种情况下,我们预测目标变量是连续的。
与决策树相关的重要术语
1.根节点(root node):它代表整个成员或样本,这些成员或样本会进一步被分成两个或多个同类型的集合。
2.分离Splitting):将一个节点拆分为两个或多个子节点的过程。
3.决策节点(Decision Node):当一个子节点分裂成更多的子节点时,它被称为决策节点。
4.叶子/终端节点(Leaf / Terminal Node):不可拆分的节点称为叶子或终端节点。
5.修剪(Pruning):我们删除一个决策节点的子节点的过程被称为修剪。也可以把修建看作是分离的反过程。
6.分支/子树(Branch / Sub-Tree):整个树的一个子部分称为分支或子树。
7.父节点和子节点(Parent and Child Node):节点可以拆分出子节点的节点称为父节点,子节点是父节点的子节点。
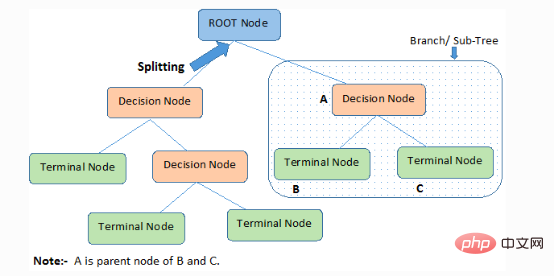
决策树通过从根到叶/终端节点的降序方式来对样本进行分类,叶/终端节点提供样品的分类方式。树中的每个节点都充当某个属性的测试用例,从节点的每个降序方向都对应着测试用例的可能答案。这个过程本质上是递归的过程,并且对每个在新节点上扎根的子树采用相同的处理方式。
创建决策树时所进行的假设
以下是我们在使用决策树时所做的一些假设:
●首先,将整个训练集作为根。
●特征值最好是可以分类的。如果这些值是连续的,那么在建立模型之前可以对它们进行离散化处理。
●记录是基于属性值递归分布的。
●通过使用一些统计方法来把相应属性按顺序放置在树的根节点或者树的内部节点。
决策树遵循乘积和表述形式。乘积和(SOP)也被称为析取范式。对于一个类,从树根到具有相同类的叶节点的每个分支都是值的合取,在该类中结束的不同分支构成了析取。
决策树实现过程中的主要挑战是确定根节点及每一级节点的属性,这个问题就是属性选择问题。目前有不同的属性选择方法来选择每一级节点的属性。
决策树是如何工作的?
决策的分离特性严重影响树的准确性,分类树和回归树的决策标准不同。
决策树使用多种算法来决定将一个节点分成两个或多个子节点。子节点的创建增加了子节点的同质性。换句话说,相对于目标变量来说,节点的纯度增加了。决策树将所有可用变量上的节点进行分离,然后选择可以产生很多同构子节点的节点进行拆分。
算法是基于目标变量的类型进行选择的。接下来,让我们看一看决策树中会使用到的一些算法:
ID3→(D3的延伸)
C4.5→(ID3的继承者)
CART→(分类与回归树)
CHAID→(卡方自动交互检测(Chi-square automatic interaction detection)在计算分类树时进行多级分离)
MARS→(多元自适应回归样条)
ID3算法使用自顶向下的贪婪搜索方法,在不回溯的情况下,通过可能的分支空间构建决策树。贪婪算法,顾名思义,总是某一时刻做出似乎是最好的选择。
ID3算法步骤:
1.它以原始集合S作为根节点。
2.在算法的每次迭代过程中,对集合S中未使用的属性进行迭代,计算该属性的熵(H)和信息增益(IG)。
3.然后选择熵最小或信息增益最大的属性。
4.紧接着用所选的属性分离集合S以产生数据的子集。
5.该算法继续在每个子集上迭代,每次迭代时只考虑以前从未选择过的属性。
属性选择方法
如果数据集包含N个属性,那么决定将哪个属性放在根节点或放在树的不同级别作为内部节点是一个复杂的步骤。通过随机选择任意节点作为根结点并不能解决问题。如果我们采用随机的方法,可能会得到比较糟糕的结果。
为了解决这一属性选择问题,研究人员设计了一些解决方案。他们建议使用如下标准:
- 熵
- 信息增益
- 基尼指数
- 增益率
- 方差削减
- 卡方
使用这些标准计算每个属性的值,然后对这些值进行排序,并将属性按照顺序放置在树中,也就是说,高值的属性放置在根位置。
在使用信息增益作为标准时,我们假设属性是分类的,而对于基尼指数,我们假设属性是连续的。
1. 熵
熵是对被处理信息的随机性的度量。熵值越高,就越难从信息中得出任何结论。抛硬币就是提供随机信息的行为的一个例子。
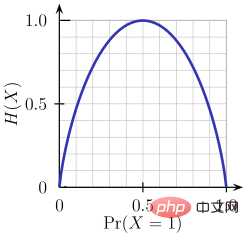
由上图可知,当概率为0或1时,熵H(X)为零。当概率为0.5时,熵是最大的,因为它在数据中投射出完全的随机性。
ID3遵循的规则是:一个熵为0的分支是一个叶节点,一个熵大于0的分支需要进一步分离。
单个属性的数学熵表示如下:

其中S表示当前状态,Pi表示状态S中事件i的概率或状态S节点中i类的百分比。
多个属性的数学熵表示如下:
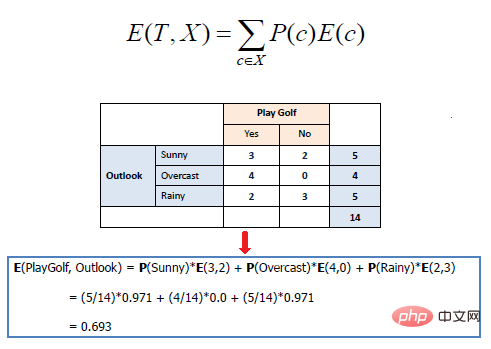
其中T表示当前状态,X表示选定属性
2.信息增益
信息增益(Information gain, IG)是一种统计属性,用来衡量给定属性根据目标类分离训练的效果。构建决策树就是寻找一个返回最高信息增益和最小熵的属性的过程。
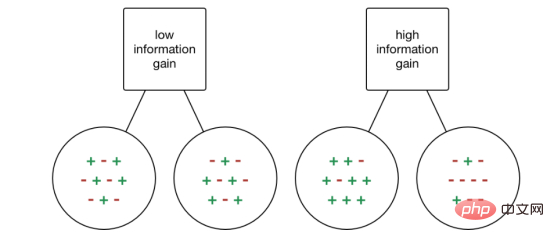
信息的增加就是熵的减少。它根据给定的属性值计算数据集分离前的熵差和分离后的平均熵差。ID3决策树算法使用的就是信息增益的方法。
IG在数学上表示如下:

用一种更简单的方法,我们可以得出这样的结论:
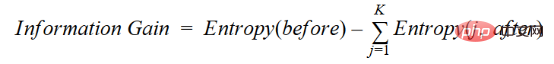
其中before为拆分前的数据集,K为拆分产生的子集数量,(j, after)为拆分后的子集j。
3.基尼指数
您可以将基尼指数理解为用于评估数据集中分离的成本函数。它的计算方法是用1减去每个类的概率平方和。它倾向于较大的分区并且易于实现的情形,而信息增益则倾向于具有不同值的较小分区的情形。
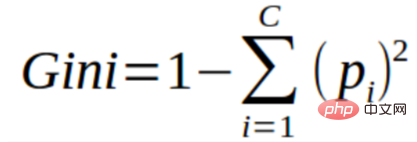
基尼指数离不开分类目标变量“成功”或“失败”。它只执行二进制分离。基尼系数越高,不平等程度越高,异质性越强。
计算基尼指数分离的步骤如下:
- 计算子节点的基尼系数,使用上面的成功(p)和失败(q)的公式(p²+q²)。
- 使用分离的每个节点的加权基尼得分计算分离的基尼系数指数。
CART(Classification and Regression Tree)就是使用基尼指数方法来创建分离点。
4.增益率
信息增益倾向于选择具有大量值的属性作为根节点。这意味着它更喜欢具有大量不同值的属性。
C4.5是ID3的改进方法,它使用增益比,这是对信息增益的一种修正,以减少其偏置,通常是最好的选择方法。增益率克服了信息增益的问题,在进行拆分之前考虑了分支的数量。它通过考虑分离的内在信息来纠正信息增益。
假如我们有一个数据集,其中包含用户和他们的电影类型偏好,这些偏好基于性别、年龄组、等级等变量。在信息增益的帮助下,你将在“性别”中进行分离(假设它拥有最高的信息增益),现在变量“年龄组”和“评级”可能同样重要,在增益比的帮助下,我们可以选择在下一层中进行分离的属性。
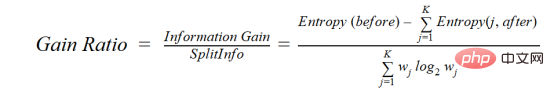
其中before为分离前的数据集,K为分离产生的子集数量,(j, after)为分离后的子集j。
5.方差削减
方差削减是一种用于连续目标变量(回归问题)的算法。该算法使用标准方差公式来选择最佳分离方式。选择方差较低的分离作为分离总体的标准:
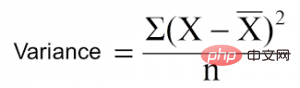
是均值,X是实际值,n是值的个数。
计算方差的步骤:
- 计算每个节点的方差。
- 计算每一次分离的方差并作为每个节点方差的加权平均。
6.卡方
CHAID是Chi-squared Automatic Interaction Detector的缩写。这是比较老的树的分类方法之一。找出子节点与父节点之间的差异具有统计学意义。我们通过对目标变量的观测频率和期望频率之间的标准化差的平方和来衡量它。
它与分类目标变量“成功”或“失败”一起工作。它可以执行两次或多次分离。卡方值越高,子节点与父节点之间的差异统计意义就越高。它生成一个名为CHAID的树。
在数学上,Chi-squared表示为:

计算卡方的步骤如下:
- 通过计算成功和失败的偏差来计算单个节点的卡方
- 使用分离的各节点的成功和失败的所有卡方之和计算分离的卡方
如何避免/对抗决策树的过拟合(Overfitting)?
决策树存在一个常见问题,特别是对于一个满列的树。有时它看起来像是树记住了训练数据集。如果一个决策树没有限制,它会给你100%的训练数据集的准确性,因为在最糟糕的情况下,它最终会为每个观察产生一个叶子。因此,当预测不属于训练集的样本时,这就会影响准确性。
在此我介绍两种方法来消除过拟合,分别是修剪决策树和随机森林。
1.修剪决策树
分离过程会产生完全长成的树,直到达到停止标准。但是,成熟的树很可能会过度拟合数据,导致对未见数据的准确性较差。

在修剪中,你剪掉树的分支,也就是说,删除从叶子节点开始的决策节点,这样整体的准确性就不会受到干扰。这是通过将实际的训练集分离为两个集:训练数据集D和验证数据集V,用分离的训练数据集D准备决策树,然后继续对树进行相应的修剪,以优化验证数据集V的精度。
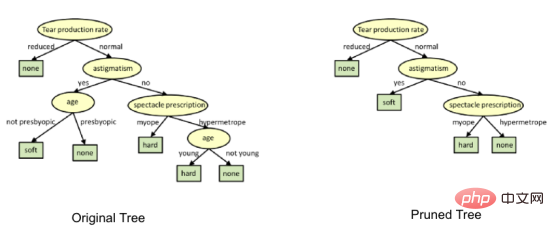
在上图中,树左侧的“Age”属性已经被修剪,因为它在树的右侧更重要,因此消除了过拟合。
2.随机森林
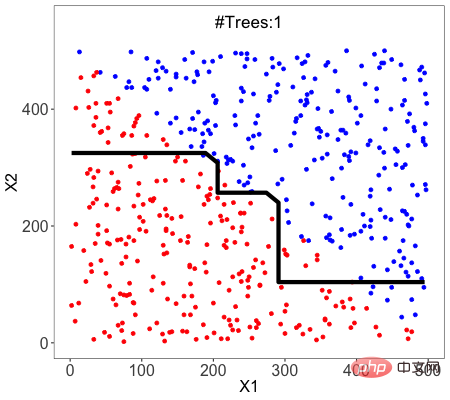
随机森林是集成学习(Ensemble Learning)的一个例子,我们结合多种机器学习算法来获得更好的预测性能。因为构建树时训练数据集是随机抽样的,且分离节点时考虑特征的随机子集,所以我们把这种方法称之为随机。
一种被称为bagging的技术被用来创建一个树的集合,其中多个训练集通过替换生成。
bagging技术采用随机抽样的方法将数据集划分为N个样本。然后,使用单一学习算法在所有样本上建立模型。之后通过并行投票或平均的方式将预测结果结合起来。
线性模型和基于树的模型哪个更好?
该问题取决于你要解决的问题类型。
1.如果因变量和自变量之间的关系可以被一个线性模型很好地模拟,线性回归将优于基于树的模型。
2.如果因变量和自变量之间存在高度的非线性且复杂的关系,树模型将优于经典回归方法。
3.如果你需要建立一个容易理解的模型,决策树模型总是比线性模型更好。决策树模型比线性回归更容易理解!
使用Scikit-learn进行决策树分类器构建
我采用的数据是从https://drive.google.com/open?id=1x1KglkvJxNn8C8kzeV96YePFnCUzXhBS下载的超市相关数据,首先使用下面的代码加载所有基本库:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
之后,我们采用下面的方式加载数据集。它包括5个属性,用户id,性别,年龄,预估工资和购买情况。
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()
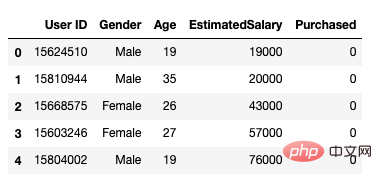
图1数据集
我们只将年龄和预估工资作为我们的自变量X,因为性别和用户ID等其他特征是不相关的,对一个人的购买能力没有影响,y是因变量。
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
下一步是将数据集分离为训练集和测试集。
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
接下来执行特征缩放
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
将模型拟合到决策树分类器中。
from sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
进行预测并检查准确性。
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))
决策树分类器的准确率达到91%。
混淆矩阵
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])
这意味着有6个观测结果被列为错误。
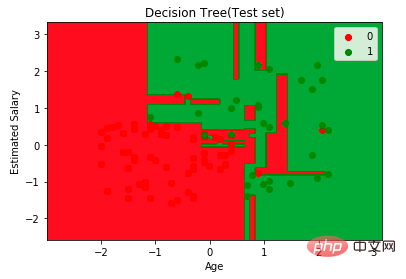
首先,让我们将模型预测结果可视化
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()
接下来,想象一下这棵树
接下来您可以使用Scikit-learn的export_graphviz函数在Jupyter笔记本中显示树。为了绘制树,我们需要采用下面的命令安装Graphviz和pydotplus:
conda install python-graphviz pip install pydotplus
export_graphviz函数将决策树分类器转换为点文件,pydotplus将该点文件转换为png或在Jupyter上显示的形式,具体实现方式如下:
from sklearn.tree import export_graphviz from sklearn.externals.six import StringIO from IPython.display import Image import pydotplusdot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True,feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
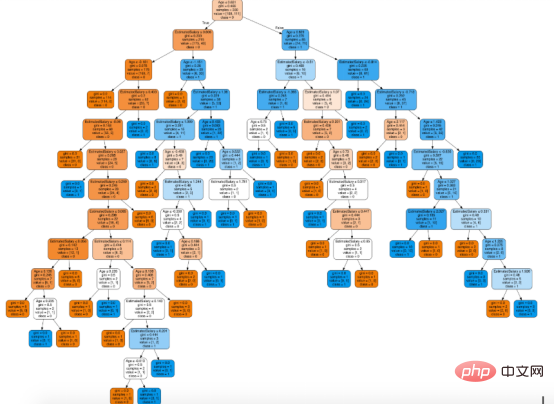
在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
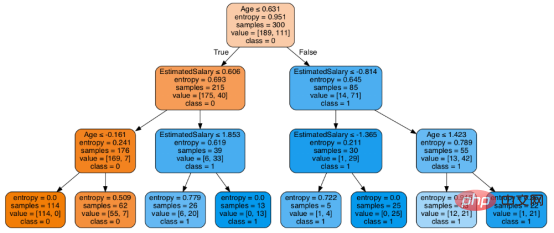
上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
以上是剖析决策树算法的详细内容。更多信息请关注PHP中文网其他相关文章!
 优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM
优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM介绍 恭喜!您经营一家成功的业务。通过您的网页,社交媒体活动,网络研讨会,会议,免费资源和其他来源,您每天收集5000个电子邮件ID。下一个明显的步骤是
 Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM
Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM介绍 在当今快节奏的软件开发环境中,确保最佳应用程序性能至关重要。监视实时指标,例如响应时间,错误率和资源利用率可以帮助MAIN
 Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM“您有几个用户?”他扮演。 阿尔特曼回答说:“我认为我们上次说的是每周5亿个活跃者,而且它正在迅速增长。” “你告诉我,就像在短短几周内翻了一番,”安德森继续说道。 “我说那个私人
 pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介绍 Mistral发布了其第一个多模式模型,即Pixtral-12b-2409。该模型建立在Mistral的120亿参数Nemo 12B之上。是什么设置了该模型?现在可以拍摄图像和Tex
 生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
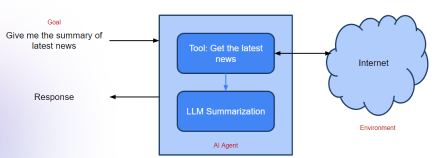
生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想象一下,拥有一个由AI驱动的助手,不仅可以响应您的查询,还可以自主收集信息,执行任务甚至处理多种类型的数据(TEXT,图像和代码)。听起来有未来派?在这个a


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

Atom编辑器mac版下载
最流行的的开源编辑器

ZendStudio 13.5.1 Mac
功能强大的PHP集成开发环境

SublimeText3汉化版
中文版,非常好用

WebStorm Mac版
好用的JavaScript开发工具

VSCode Windows 64位 下载
微软推出的免费、功能强大的一款IDE编辑器