AI驱动运筹优化「光刻机」！中科大等提出分层序列模型，大幅提升数学规划求解效率

数学规划求解器因其重要性和通用性，被誉为运筹优化领域的「光刻机」。

其中，混合整数线性规划 (Mixed-Integer Linear Programming, MILP) 是数学规划求解器的关键组件，可建模大量实际应用，如工业排产，物流调度，芯片设计，路径规划，金融投资等重大领域。

近期，中科大 MIRA Lab 王杰教授团队和华为诺亚方舟实验室联合提出分层序列模型（Hierarchical Sequence Model, HEM），大幅提升混合整数线性规划求解器求解效率，相关成果发表于ICLR 2023。

目前，算法已整合入华为 MindSpore ModelZoo 模型库，相关技术和能力并将于今年内整合入华为天筹（OptVerse）AI求解器。该求解器旨在将运筹学和AI相结合，突破业界运筹优化极限，助力企业量化决策和精细化运营，实现降本增效！

作者列表：王治海*，李希君*，王杰**，匡宇飞，袁明轩，曾嘉，张勇东，吴枫

论文链接：https://openreview.net/forum?id=Zob4P9bRNcK

开源数据集：https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing

PyTorch 版本开源代码：https://github.com/MIRALab-USTC/L2O-HEM-Torch

MindSpore 版本开源代码：https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut

天筹（OptVerse）AI求解器：https://www.huaweicloud.com/product/modelarts/optverse.html

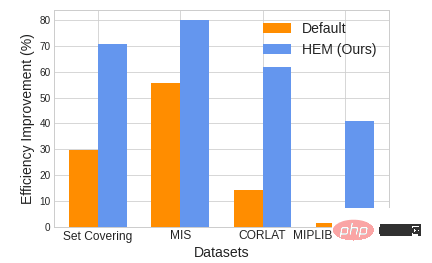
图1. HEM 与求解器默认策略（Default）求解效率对比，HEM 求解效率最高可提升 47.28%

1 引言

割平面（cutting planes, cuts）对于高效求解混合整数线性规划问题至关重要。

其中割平面选择（cut selection）旨在选择待选割平面的恰当子集以提高求解 MILP 的效率。割平面选择在很大程度上取决于两个子问题： （P1）应优先选哪些割平面，以及（P2）应选择多少割平面。

尽管许多现代 MILP 求解器通过手动设计的启发式方法来处理 (P1) 和 (P2)，但机器学习方法有潜力学习更有效的启发式方法。

然而，许多现有的学习类方法侧重于学习应该优先选择哪些割平面，而忽略了学习应该选择多少割平面。此外，我们从大量的实验结果中观察到又一子问题，即（P3）应该优先选择哪种割平面顺序，对求解 MILP 的效率也有重大影响。

为了应对这些挑战，我们提出了一种新颖的分层序列模型（Hierarchical Sequence Model, HEM），并通过强化学习框架来学习割平面选择策略。

据我们所知，HEM 是首个可同时处理（P1），（P2）和（P3）的学习类方法。实验表明，在人工生成和大规模真实世界 MILP 数据集上，与人工设计和学习类基线相比，HEM 大幅度提高了求解 MILP 的效率。

2 背景与问题介绍

2.1 割平面（cutting planes, cuts）介绍

混合整数线性规划（Mixed-Integer Linear Programming, MILP）是一种可广泛应用于多种实际应用领域的通用优化模型，例如供应链管理 [1]、排产规划 [2]、规划调度 [3]、工厂选址 [4]、装箱问题 [5]等。

标准的MILP具有以下形式：

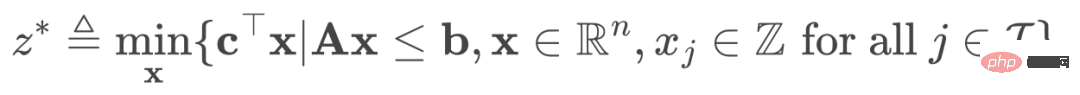
（1）

给定问题（1），我们丢弃其所有整数约束，可得到线性规划松弛（linear programming relaxation, LPR）问题，它的形式为：

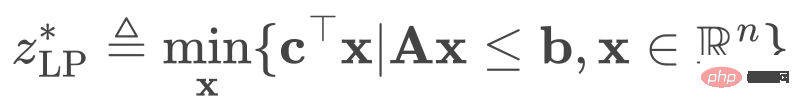
（2）

由于问题（2）扩展了问题（1）的可行集，因此我们可有，即 LPR 问题的最优值是原 MILP 问题的下界。

给定（2）中的 LPR 问题，割平面（cutting planes, cuts）是一类合法线性不等式，这些不等式在添加到线性规划松弛问题中后，可收缩 LPR 问题中的可行域空间，且不去除任何原 MILP 问题中的整数可行解。

2.2 割平面选择（cut selection）介绍

MILP 求解器在求解 MILP 问题过程中可生成大量的割平面，且会在连续的回合中不断向原问题中添加割平面。

具体而言，每一回合中包括五个步骤：

（1）求解当前的 LPR 问题；

（2）生成一系列待选割平面；

（3）从待选割平面中选择一个合适的子集；

（4）将选择的子集添加到 (1) 中的 LPR 问题，以得到一个新的 LPR 问题；

（5）循环重复，基于新的 LPR 问题，进入下一个回合。

将所有生成的割平面添加到 LPR 问题中可最大程度地收缩该问题的可行域空间，以最大程度提高下界。

然而，添加过多的割平面可能会导致问题约束过多，增加问题求解计算开销并出现数值不稳定问题 [6,7]。

因此，研究者们提出了割平面选择（cut selection），割平面选择旨在选择候选割平面的适当子集，以尽可能提升 MILP 问题求解效率。割平面选择对于提高解决混合整数线性规划问题的效率至关重要 [8,9,10]。

2.3 启发实验——割平面添加顺序

我们设计了两种割平面选择启发式算法，分别为 RandomAll 和 RandomNV（详见原论文第3章节）。

它们都在选择了一批割平面后，以随机顺序将选择的割平面添加到 MILP 问题中。如图2结果显示，选定同一批割平面的情况下，以不同的顺序添加这些选定割平面对求解器求解效率有极大的影响（详细结果分析见原论文第3章节）。

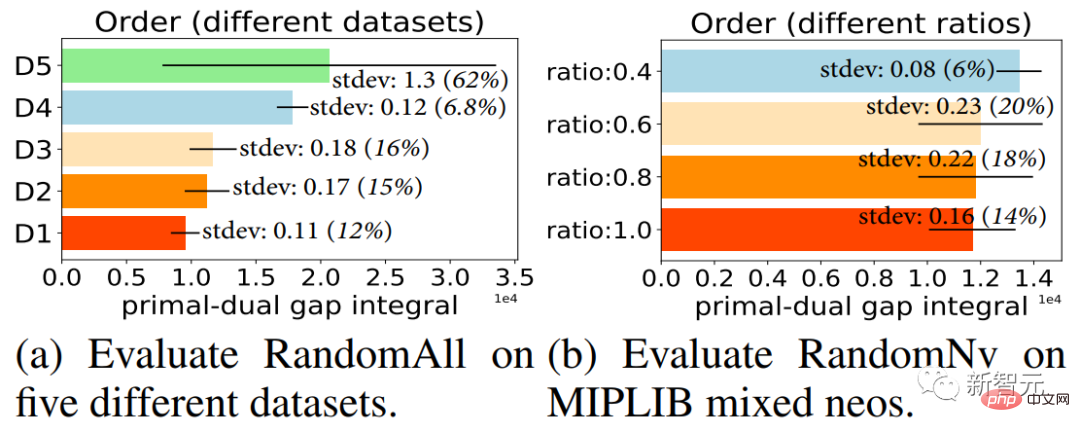
图2. 每一个柱子代表在求解器中，选定相同的一批割平面，以10轮不同的顺序添加这些选定割平面，求解器最终的求解效率的均值，柱子中的标准差线代表不同顺序下求解效率的标准差。标准差越大，代表顺序对求解器求解效率影响越大。

3 方法介绍

在割平面选择任务中，应该选择的最优子集是不可事先获取的。

不过，我们可以使用求解器评估所选任意子集的质量，并以此评估作为学习算法的反馈。

因此，我们利用强化学习（Reinforcement Learning, RL）范式来试错学习割平面选择策略。

在本节中，我们详细阐述了我们提出的 RL 框架。

首先，我们将割平面选择任务建模为马尔科夫决策过程（Markov Decision Process, MDP）；然后，我们详细介绍我们提出的分层序列模型（hierarchical sequence model, HEM）；最后，我们推导可高效训练 HEM 的分层策略梯度。我们整体的 RL 框架图如图3所示。

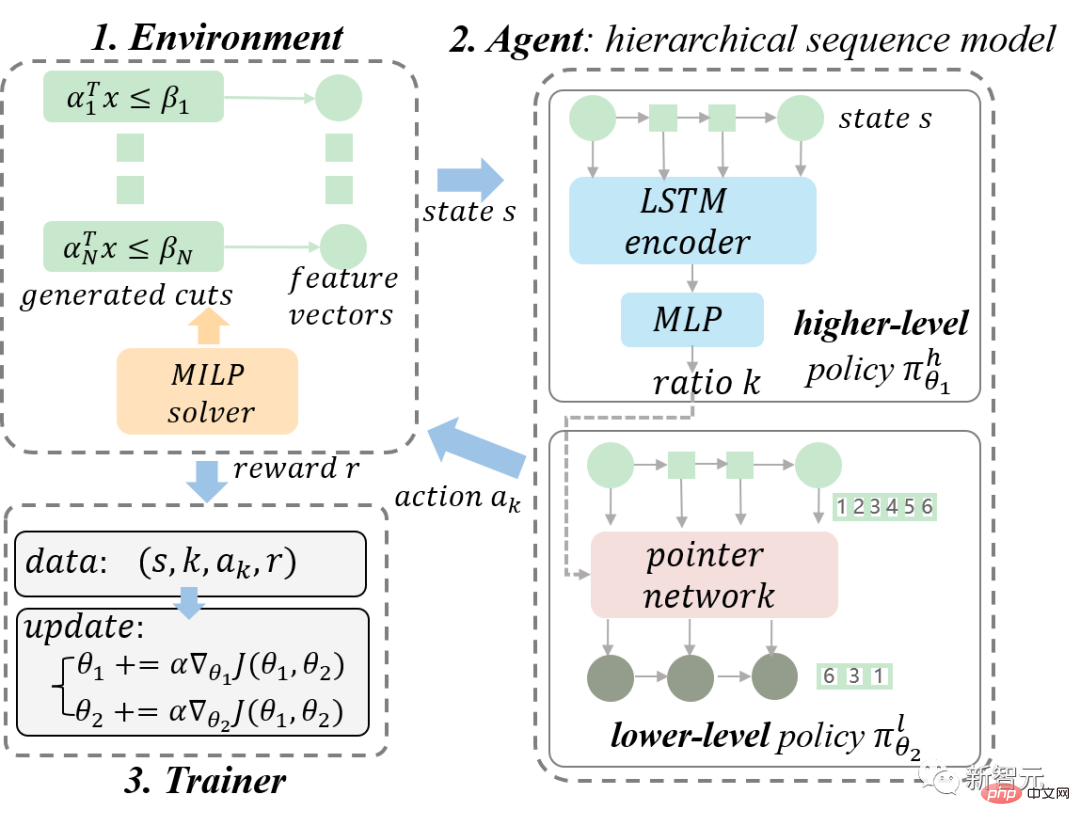
图3. 我们所提出的整体 RL 框架图。我们将 MILP 求解器建模为环境，将 HEM 模型建模为智能体。我们通过智能体和环境不断交互采集训练数据，并使用分层策略梯度训练 HEM 模型。

3.1 问题建模

状态空间：由于当前的 LP 松弛和生成的待选 cuts 包含割平面选择的核心信息，我们通过定义状态。这里  表示当前 LP 松弛的数学模型， 表示候选割平面的集合，表示 LP 松弛的最优解。为了编码状态信息，我们根据的信息为每个待选割平面设计13个特征。也就是说，我们通过一个13维特征向量来表示状态 s。具体细节请见原文第4章节。

动作空间：为了同时考虑所选 cut 的比例和顺序，我们以候选割平面集合的所有有序子集定义动作空间。

奖励函数：为了评估添加 cut 对求解 MILP 的影响，我们可通过求解时间，原始对偶间隙积分（primal-dual gap integral），对偶界提升（dual bound improvement）。具体细节请见原文第4章节。

转移函数：转移函数给定当前状态和采取的动作，输出下一状态。割平面选择任务中转移函数隐式地由求解器提供。

更多建模细节请见原文第4章节。

3.2 策略模型：分层序列模型

如图3所示，我们将 MILP 求解器建模为环境，将 HEM 建模为智能体，下面详细介绍所提出的 HEM 模型。为了方便阅读，我们简化方法动机，聚焦于讲清楚方法实现，欢迎感兴趣的读者参见原论文第4章节，了解相关细节。

如图3中 Agent 模块所示，HEM 由上下层策略模型组成。上下层模型分别学习上层策略（policy）  和下层policy 。

首先，上层策略通过预测恰当的比例来学习应该选择的 cuts 的数量。假设状态长度为，预测比率为，那么预测应该选择的 cut 数为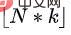

，其中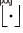表示向下取整函数。我们定义。

其次，下层策略学习选择给定大小的有序子集。下层策略可以定义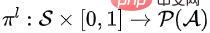，其中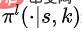表示给定状态S和比例K的动作空间上的概率分布。具体来说，我们将下层策略建模为一个序列到序列模型（sequence to sequence model, sequence model）。

最后，通过全概率定律推导出 cut 选择策略，即

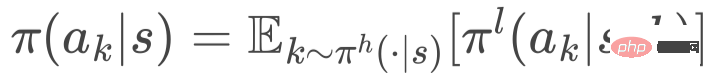
3.3 训练方法：分层策略梯度

给定优化目标函数

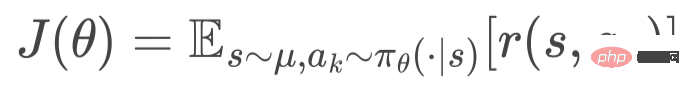
图4. 分层策略梯度。我们以此随机梯度下降的方式优化 HEM 模型。

4 实验介绍

我们的实验有五个主要部分：

实验1. 在3个人工生成的MILP问题和来自不同应用领域的6个具有挑战性的MILP问题基准上评估我们的方法。

实验2. 进行精心设计的消融实验，以提供对HEM的深入洞察。

实验3. 测试 HEM 针对问题规模的泛化性能。

实验4. 可视化我们的方法与基线所选择的割平面特点。

实验5. 将我们的方法部署到华为实际的排产规划问题中，验证 HEM 的优越性。

我们在此文章中只介绍实验1，更多实验结果，请参见原论文第5章节。请注意，我们论文中汇报的所有实验结果都是基于 PyTorch 版本代码训练得到的结果。

实验1结果如表1所示，我们在9个开源数据集上对比了 HEM 和6个基线的对比结果。实验结果显示，HEM 可平均提升约 20% 求解效率。

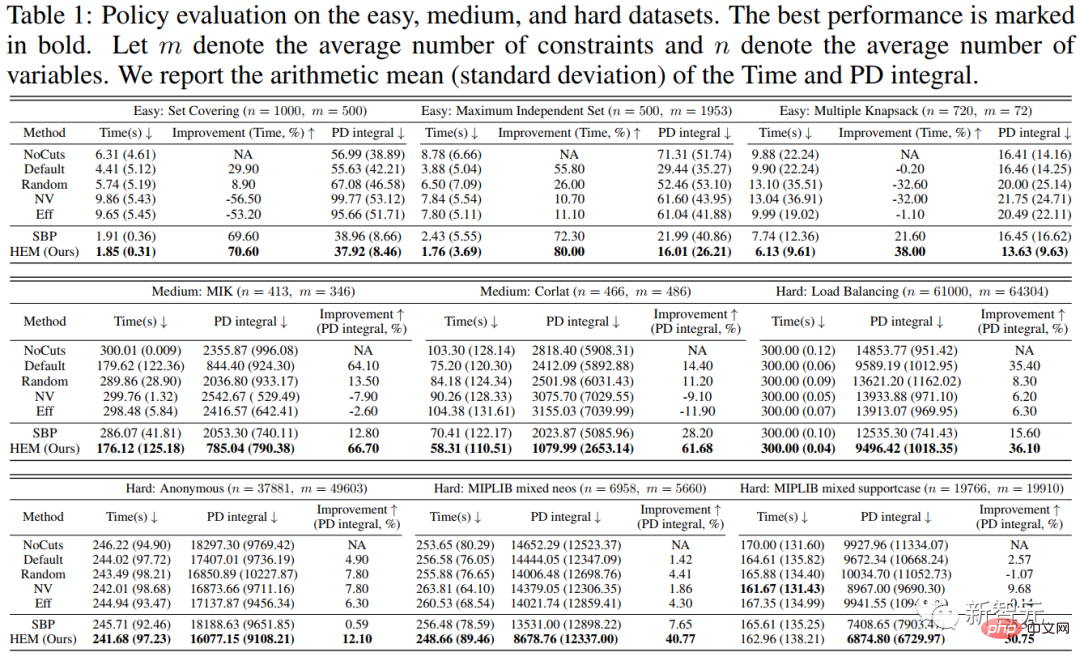
图5. 对easy、medium 和 hard 数据集的策略评估。最优性能我们用粗体字标出。以m表示约束条件的平均数量，n表示变量的平均数量。我们展示了求解时间和primal-dual gap 积分的算术平均值（标准偏差）。

以上是AI驱动运筹优化「光刻机」！中科大等提出分层序列模型，大幅提升数学规划求解效率的详细内容。更多信息请关注PHP中文网其他相关文章！