一文详解Python数据分析模块Numpy切片、索引和广播

Numpy切片和索引

ndarray对象的内容可以通过索引或切片来访问和修改，与 Python 中 list 的切片操作一样。

ndarray 数组可以基于 0 ~ n-1 的下标进行索引，切片对象可以通过内置的 slice 函数，并设置 start, stop 及 step 参数进行，从原数组中切割出一个新数组。

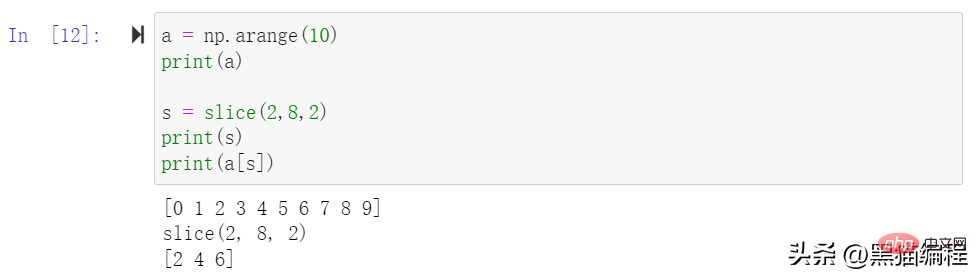
切片还可以包括省略号 …，来使选择元组的长度与数组的维度相同。 如果在行位置使用省略号，它将返回包含行中元素的 ndarray。

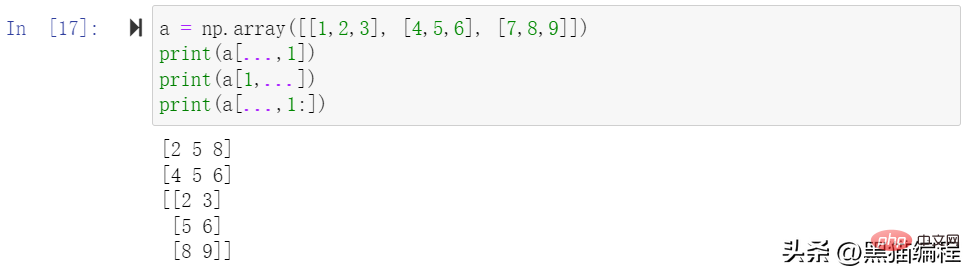
高级索引

整数数组索引

以下实例获取数组中 (0,0)，(1,1) 和 (2,0) 位置处的元素。

a = np.array([[0,1,2], [3,4,5], [6,7,8], [9,10,11]])
print(a)
print('-' * 20)

rows = np.array([[0,0], [3,3]])
cols = np.array([[0,2], [0,2]])

b = a[rows, cols]
print(b)
print('-' * 20)

rows = np.array([[0,1], [2,3]])
cols = np.array([[0,2], [0,2]])
c = a[rows, cols]
print(c)
print('-' * 20)

rows = np.array([[0,1,2], [1,2,3], [1,2,3]])
cols = np.array([[0,1,2], [0,1,2], [0,1,2]])
d = a[rows, cols]
print(d)

[[ 012]
 [ 345]
 [ 678]
 [ 9 10 11]]
--------------------
[[ 02]
 [ 9 11]]
--------------------
[[ 05]
 [ 6 11]]
--------------------
[[ 048]
 [ 37 11]
 [ 37 11]]

返回的结果是包含每个角元素的 ndarray 对象。

可以借助切片 : 或 … 与索引数组组合。如下面例子：

a = np.array([[1,2,3], [4,5,6], [7,8,9]])

print(a)
print('-' * 20)

b = a[1:3, 1:3]
print(b)
print('-' * 20)

c = a[1:3, [0,2]]
print(c)
print('-' * 20)

d = a[..., 1:]
print(d)

[[1 2 3]
 [4 5 6]
 [7 8 9]]
--------------------
[[5 6]
 [8 9]]
--------------------
[[4 6]
 [7 9]]
--------------------
[[2 3]
 [5 6]
 [8 9]]

布尔索引

我们可以通过一个布尔数组来索引目标数组。

布尔索引通过布尔运算（如：比较运算符）来获取符合指定条件的元素的数组。

以下实例获取大于 5 的元素：

a = np.array([[1,2,3], [4,5,6], [7,8,9]])

print(a)
print('-' * 20)

print(a[a > 5])

[[1 2 3]
 [4 5 6]
 [7 8 9]]
--------------------
[6 7 8 9]

以下实例使用了 ~（取补运算符）来过滤 NaN。

a = np.array([np.nan, 1, 2, np.nan, 3, 4, 5])

print(a)
print('-' * 20)

print(a[~np.isnan(a)])

[nan1.2. nan3.4.5.]
--------------------
[1. 2. 3. 4. 5.]

以下实例演示如何从数组中过滤掉非复数元素。

a = np.array([1, 3+4j, 5, 6+7j])

print(a)
print('-' * 20)

print(a[np.iscomplex(a)])

[1.+0.j 3.+4.j 5.+0.j 6.+7.j]
--------------------
[3.+4.j 6.+7.j]

花式索引

花式索引指的是利用整数数组进行索引。

花式索引根据索引数组的值作为目标数组的某个轴的下标来取值。

对于使用一维整型数组作为索引，如果目标是一维数组，那么索引的结果就是对应位置的元素，如果目标是二维数组，那么就是对应下标的行。

花式索引跟切片不一样，它总是将数据复制到新数组中。

一维数组

a = np.arange(2, 10)

print(a)
print('-' * 20)

b = a[[0,6]]
print(b)

[2 3 4 5 6 7 8 9]
--------------------
[2 8]

二维数组

1、传入顺序索引数组

a = np.arange(32).reshape(8, 4)

print(a)
print('-' * 20)

print(a[[4, 2, 1, 7]])

[[ 0123]
 [ 4567]
 [ 89 10 11]
 [12 13 14 15]
 [16 17 18 19]
 [20 21 22 23]
 [24 25 26 27]
 [28 29 30 31]]
--------------------
[[16 17 18 19]
 [ 89 10 11]
 [ 4567]
 [28 29 30 31]]

2、传入倒序索引数组

a = np.arange(32).reshape(8, 4)
print(a[[-4, -2, -1, -7]])

[[16 17 18 19]
 [24 25 26 27]
 [28 29 30 31]
 [ 4567]]

3、传入多个索引数组（要使用 np.ix_）

np.ix_ 函数就是输入两个数组，产生笛卡尔积的映射关系。

笛卡尔乘积是指在数学中，两个集合 X 和 Y 的笛卡尔积（Cartesian product），又称直积，表示为 X×Y，第一个对象是X的成员而第二个对象是 Y 的所有可能有序对的其中一个成员。

例如 A={a,b}, B={0,1,2}，则：

A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}

a = np.arange(32).reshape(8, 4)
print(a[np.ix_([1,5,7,2], [0,3,1,2])])

[[ 4756]
 [20 23 21 22]
 [28 31 29 30]
 [ 8 119 10]]

广播(Broadcast)

广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式， 对数组的算术运算通常在相应的元素上进行。

如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同，且各维度的长度相同。

a = np.arange(1, 5)
b = np.arange(1, 5)

c = a * b
print(c)

[ 149 16]

当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制。如：

a = np.array([
[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]
])

b = np.array([0, 1, 2])

print(a + b)

[[ 012]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

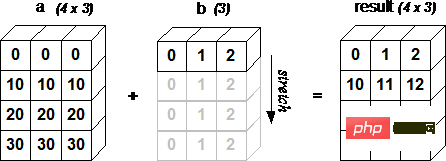
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。

tile扩展数组

a = np.array([1, 2])

b = np.tile(a, (6, 1))
print(b)

print('-' * 20)

c = np.tile(a, (2, 3))
print(c)

[[1 2]
 [1 2]
 [1 2]
 [1 2]
 [1 2]
 [1 2]]
--------------------
[[1 2 1 2 1 2]
 [1 2 1 2 1 2]]

4x3 的二维数组与长为 3 的一维数组相加，等效于把数组 b 在二维上重复 4 次再运算：

a = np.array([
[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]
])

b = np.array([0, 1, 2])
bb = np.tile(b, (4, 1))

print(a + bb)

[[ 012]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

广播的规则:

• 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分都通过在前面加 1 维补齐。
• 输出数组的形状是输入数组形状的各个维度上的最大值。
• 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错。
• 当输入数组的某个维度的长度为 1 时，沿着此维度运算时都用此维度上的第一组值。

简单理解：对两个数组，分别比较他们的每一个维度（若其中一个数组没有当前维度则忽略），满足：

• 数组拥有相同形状。
• 当前维度的值相等。
• 当前维度的值有一个是 1。

若条件不满足，抛出 "ValueError: frames are not aligned" 异常。

以上是一文详解Python数据分析模块Numpy切片、索引和广播的详细内容。更多信息请关注PHP中文网其他相关文章！