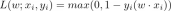数学推理是人类智能的一项核心能力,但对于机器来说,抽象思维和逻辑推理仍然是一个很大的挑战。大规模预训练语言模型,如 GPT-3 和 GPT-4,在文本形式的数学推理(如数学应用题)上已经取得了显著的进展。然而,目前我们还不清楚这些模型能否处理涉及到异构信息(如表格数据)的更复杂的问题。为了填补这一空白,来自 UCLA 和艾伦人工智能研究院(AI2) 的研究人员推出了 Tabular Math Word Problems (TabMWP) ,这是一个包含了 38,431 个开放领域问题的数据集,需要同时在文本和表格数据上进行数学推理得到正确答案。TabMWP 中的每个问题都与一个上下文相关联,这个上下文包含图片、文本或结构化格式的表格。
研究人员在 TabMWP 上评估了包括 Few-shot GPT-3 等不同的预训练模型。正如已有的研究发现,Few-shot GPT-3 很依赖 in-context 示例的选择,这导致其在随机选择示例的情况下性能相当不稳定。这种不稳定在处理像 TabMWP 这样复杂的推理问题时表现得更加严重。为了解决这一问题,作者提出了 PromptPG 方法,这种方法将示例的选择转化成强化学习中的 contextual bandit 问题,并且利用 Policy Gradient 训练一个策略网络来学习从少量的训练数据中选择最优的 in-context 示例。实验结果表明,他们提出的 PromptPG 方法在回答问题的准确性上超过最优基准(Few-shot CoT GPT-3)5.31%,并且相对于随机选择的 in-context examples,他们的方法显著降低了预测的方差,提升了这类方法的稳定性。

- 论文链接:https://arxiv.org/abs/2209.14610
- 代码链接:https://github.com/lupantech/PromptPG
- 项目主页:https://promptpg.github.io
- 数据可视化:https://promptpg.github.io/explore
1、TabMWP 数据集
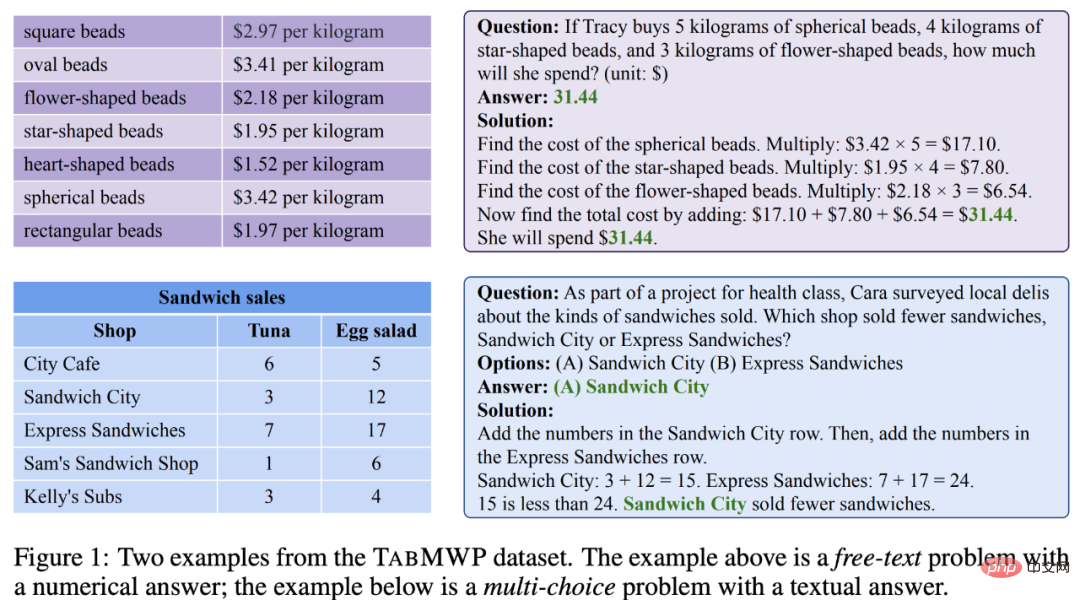
下面是来自 TabMWP 数据集的两个例子。其中一个是答案为数值类型的自由文本问题(free-text),另一个是答案为文本类型的多项选择题(multi-choice)。可以看到,每个问题都提供了一个包含分步推理的解答。要解决 TabMWP 中的问题,系统必须同时具备查表和多步数学推理的能力。举下图中的例子来说,要回答 “how much will she spend (if Tracy buys three kinds of breads)”,我们需要先在表格中查找出三种面包对应的价格,再计算购买每种面包的费用,并对它们求和已得到最终的费用。
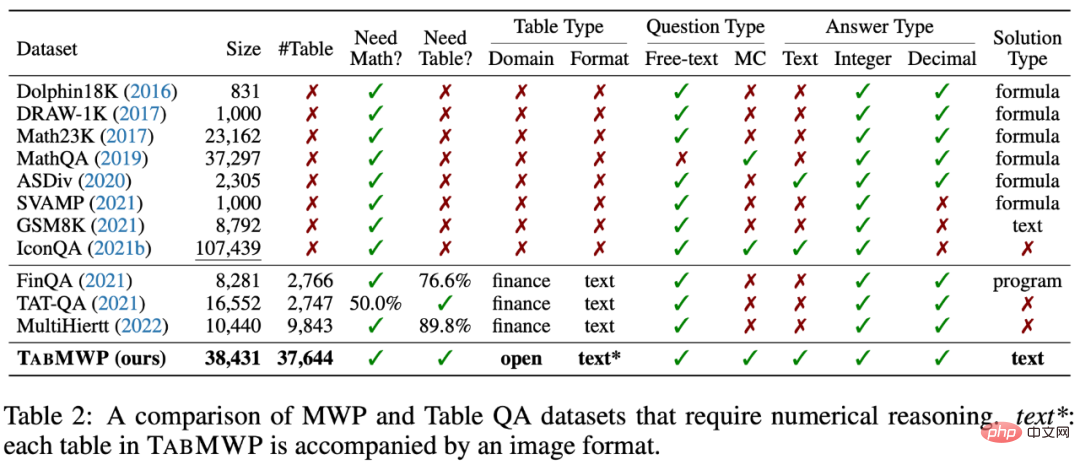
如下表的统计所示,TabMWP 数据集包含 38,431 个表格数学问题。其中 74.7% 的问题属于自由文本问题,25.3% 的问题属于多选题。TabMWP 共有 28,876 个不同的问题,6,153 个不同的答案和 35,442 个不同的解答,表明其在问题分布方面具有丰富的多样性。这些问题平均长度为 22.1 个单词,解答平均长度为 49.5 个单词,这表明 TabMWP 具有词汇的丰富性。TabMWP 的一个显著特点是,每个问题都附带有一个表格上下文,如果没有表格,问题将无法解决。TabMWP 总共有 37,644 个不同的表格,表格平均有 5.9 行和 2.2 列,12.9 个单元格,最大可达 54 个单元格。这些统计数据表明,TabMWP 中的表格也具有丰富的多样性。

TabMWP 数据集有两种不同的问题类型以及五种不同的答案类型:

TabMWP 中的每个问题都有一个表格上下文,它以图像、半结构化文本和结构化三种格式表示。这为开发不同类型的推理模型提供了可能性。
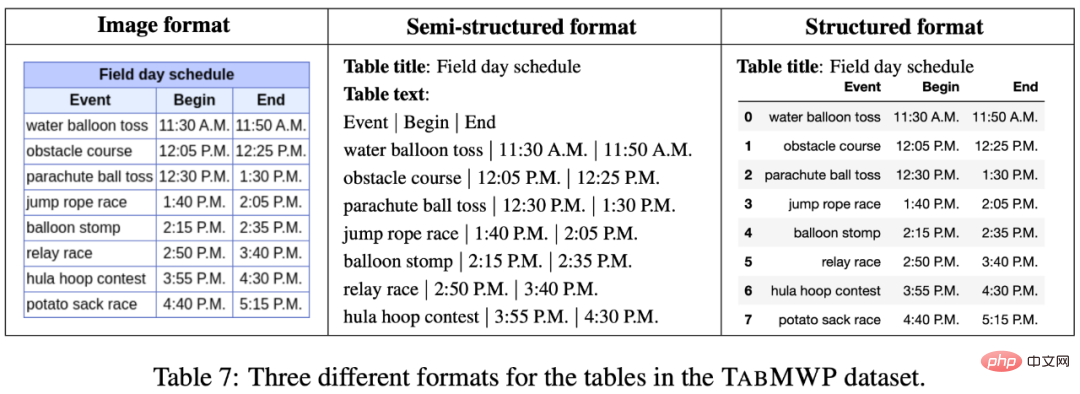
相比于已有的数据集,TabMWP 同时需要表格理解和数学推理能力来回答问题。另外,TabMWP 每道题都有详细的多步推理过程,在数据集大小、表格类型、问题类型和答案类型上有明显的优势。据本文所知,TabMWP 是第一个在开放领域表格场景下的数学推理数据集。
2、PromptPG 方法
考虑到大规模预训练模型例如 GPT-3 在解决数学应用题方面取得的成功,作者首先使用 Few-shot GPT-3 在 TabMWP 上建立了一个基准。他们从训练集中随机选择一些上下文示例以及测试样本构成提示(prompt),提示 GPT-3 预测答案。然而,最近的研究表明,这种基于随机选择的 few-shot 学习在不同的上下文示例选择上可能会表现得非常不稳定。在处理类似 TabMWP 这样的复杂推理问题时,随机选择的效果可能会更差,因为其问题涉及到不同类型和格式的表格。
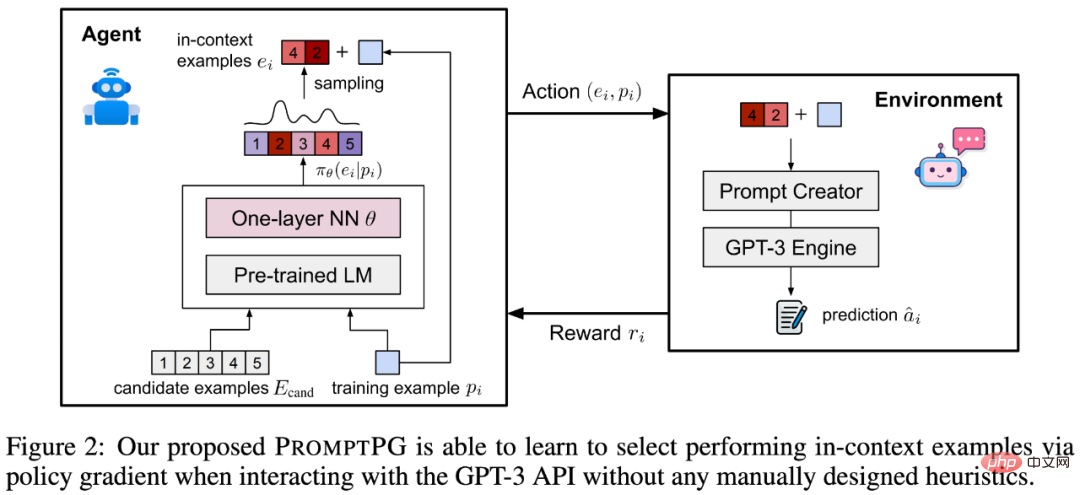
为了解决这个问题,作者提出了一种改进方法:通过 Policy Gradient 进行提示学习,从少量的训练数据中学习选择上下文示例,称为 PromptPG。如图 2 所示,策略网络学习从候选池(candidate examples)中找到最佳的 in-context example,其优化目标是在与 GPT-3 环境交互时最大化给定训练示例(training example)的预测奖励。选择示例的策略网络是一个基于固定参数的 BERT 语言模型和一个参数可学习的单层神经网络。在完成优化学习后,PromptPG 可以对不同的测试题目,动态地从候选示例中选出不同的最优示例,从而最大化提高 GPT-3 的推理性能。
以下为 PromptPG 的学习算法。

3、实验与分析

预训练与微调
表 3 对比了 PromptPG 和不同基准在 TabMWP 数据集上的结果。可以看到,TAPEX 由于在表格数据上进行了预训练,在相似参数量的前提下,其比 UnifiedQA 的表现要更好。对于 TAPEX 和 UnifiedQA 来说,提高模型的参数量都可以提高预测的准确性。此外,在 TabMWP 上进行模型的微调也可以极大地提升预测的准确性。
大规模语言模型
GPT-3 在没有任何微调的情况下(Zero-shot GPT-3),可以取得与微调过的 UnifiedQA 以及 TAPEX 模型相近的准确性。如果 Few-shot GPT-3 模型随机选择两个 in-context 示例作为 GPT-3 的提示,其相比 Zero-shot GPT-3 可以进一步提升 0.17%。通过让 Few-shot GPT-3 在生成最终答案前生成多步的中间步骤(Few-shot-CoT GPT-3),研究人员可以得到最优的基准模型,其准确率达到了 62.92%。
PromptPG
区别于随机选择 in-context 示例,本文提出的 PromptPG 通过 Policy Gradient 训练一个策略网络来选择更合适的 in-context 示例,在 TabMWP 上取得了最高的预测结果(68.23%),其平均预测准确率超过最好基准模型(Few-shot-CoT GPT-3)5.31%。值得注意的是,对于几乎所有的问题类型、答案类型和问题难度,PromptPG 都展现出了其在预测准确率上的优势。尽管如此,PromptPG 距离人类 90.22% 的表现则还有很大的提升空间。
消融实验
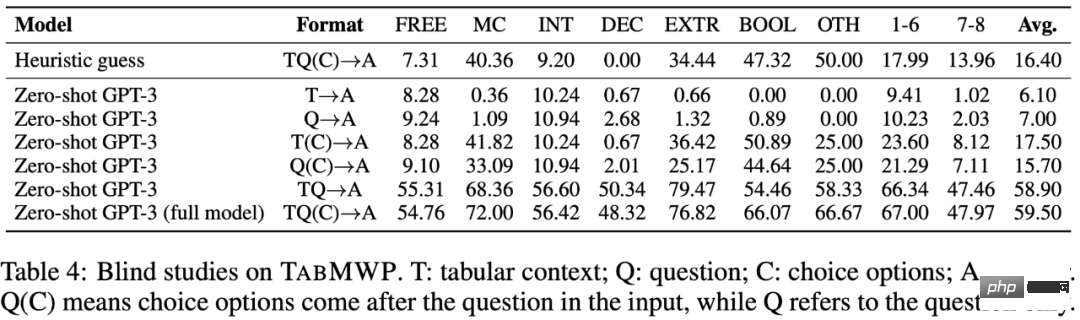
表 4 表明,TabMWP 的所有输入元素(问题文本、表格信息、选项信息)都对正确回答问题至关重要。只有所有的问题元素作为输入信息,Zero-shot GPT-3 才取得了其相对最高的平均预测准确率(59.50%)。
不同的示例选择

作为对比实验,研究人员还比较了其他不同示例选择的方法。如表 5 所示,选择与测试问题相同的题型或者答案类型可以帮助模型找到更相关的示例,并提高回答的准确性。选择最复杂的示例则并不能稳定地提高回答准确性。在候选示例中固定选择两个最好的示例,可以小幅度提高准确性,并降低方差。选择语义上最接近测试问题的示例可以达到最接近 PromptPG 方法的准确性。总体来说,PromptPG 全面展现了其在提升预测准确性和降低预测方差上的优势。
下图展示了 PromptPG 选择的示例以及最终的预测结果。可以看到,PromptPG 方法可以选择与测试题目具有类似的数学能力的示例,从而提高 Few-shot GPT-3 的推理性能。

预测成功的例子
以下展示了 PromptPG 对一个自由文本问题的正确回答。这个问题要求对表格中的八个数字分别进行加法和除法计算以得到平均值。

在如下的例子中,模型被要求理解一个税收报告,并计算扣税后的工资。

以下展示了 PromptPG 对多选题问题的正确预测。给定的表格一共有 9 行和 6 列。模型成功地定位到了表格中的目标单元格,并进行多步推理以预测正确答案。
在以下的例子中,模型需要比较预算和总成本,以验证 Ariana 是否有足够的钱。

预测失败的例子
以下展示了 PromptPG 对自由文本问题的错误预测。模型检索到了错误的玫瑰石英价格,从而错误计算了三个物品的成本总和。

在以下的例子中,问题提供了一个抽象的茎叶表。模型无法理解这个特定领域的表格,并且缺乏高级逻辑推理能力从而得到了错误的答案。

以下的例子表明,现有的模型似乎不具有对数字排序的能力。
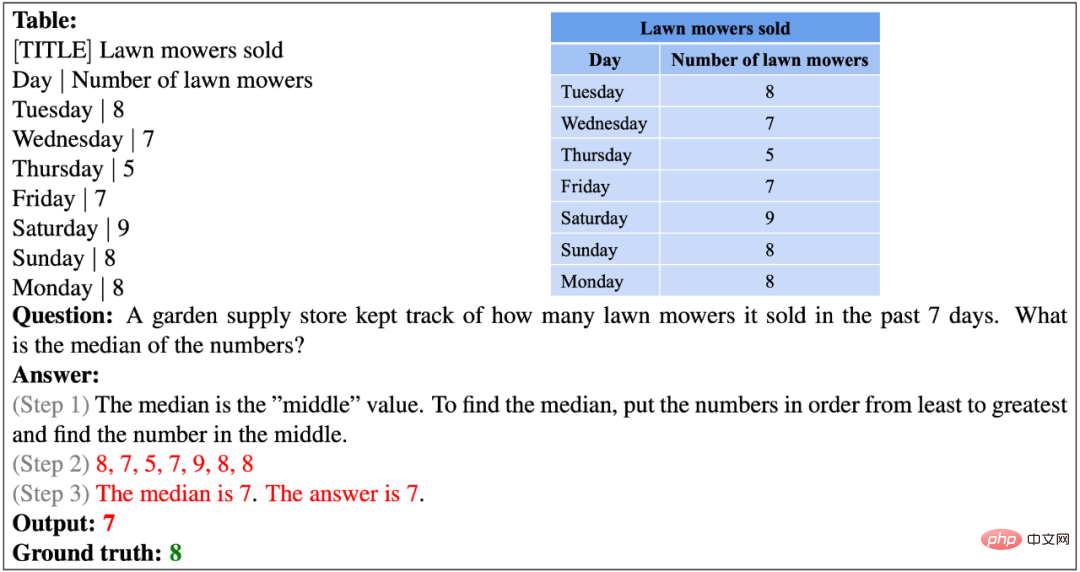
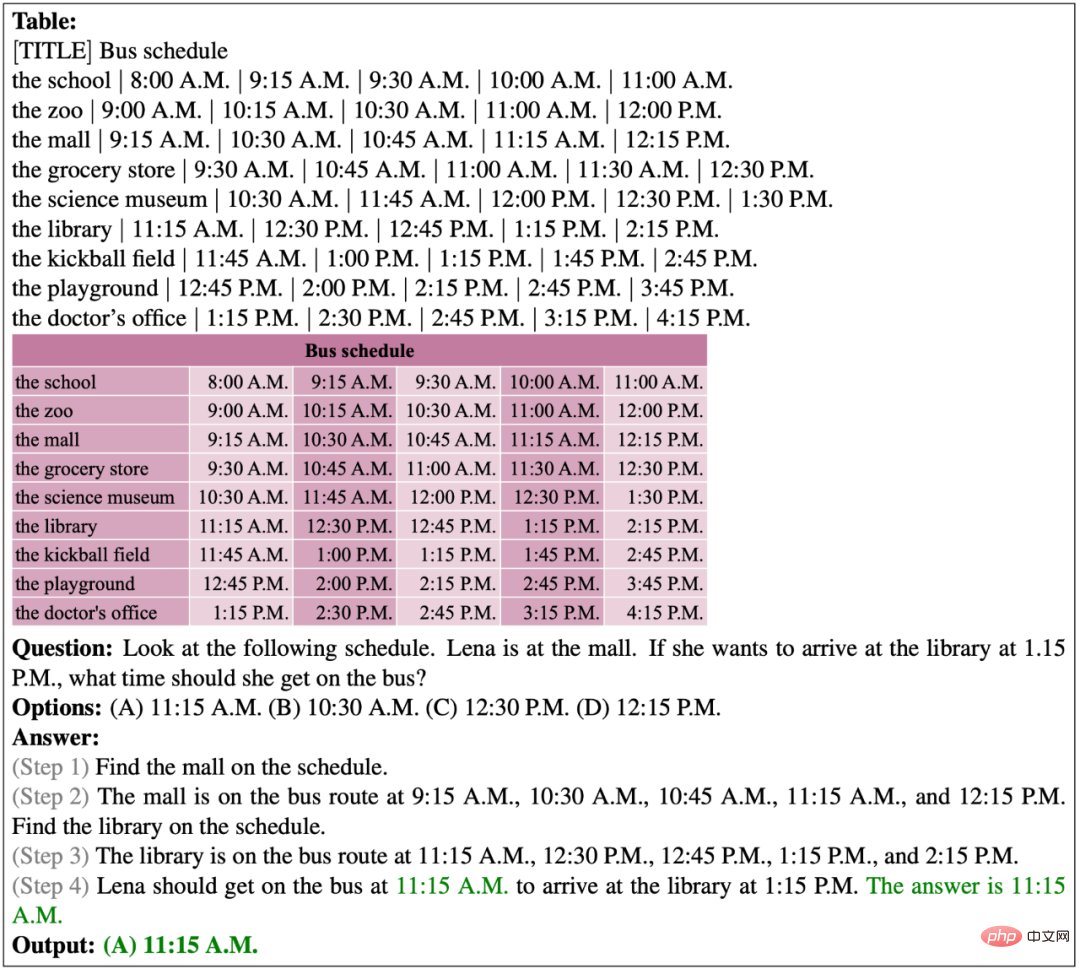
在以下的例子中,表格中没有出现与问题提到的当前时间完全一致的时间,因此模型无法准确定位到下一站的出发时间。

以下的例子中,模型很难准确完成一长串数字的算术运算。

4、结论与展望
作者提出了 TabMWP,这是第一个针对表格语境的数学问题求解的大规模数据集。TabMWP 包含了 38,431 个开放领域的问题,其中包括两种问题类型和五种答案类型,每个问题都标注了多步的解答过程。作者使用了最先进的 QA 和 TableQA 方法,在预训练和微调设置下对 TabMWP 进行了全面的实验,以及使用大型预训练语言模型 GPT-3 进行评估。作者进一步提出了一种全新的强化学习方法 PromptPG,该方法利用 Policy Gradient 学习从训练数据中选择最优的实例用于提示用于 GPT-3 模型。实验结果表明,与随机选择相比,PromptPG 的性能明显优于现有的基线,并且减少了预测中的性能不稳定性。
以上是PromptPG:当强化学习遇见大规模语言模型的详细内容。更多信息请关注PHP中文网其他相关文章!
 优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM
优化您的组织与Genai代理商的电子邮件营销Apr 13, 2025 am 11:44 AM介绍 恭喜!您经营一家成功的业务。通过您的网页,社交媒体活动,网络研讨会,会议,免费资源和其他来源,您每天收集5000个电子邮件ID。下一个明显的步骤是
 Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM
Apache Pinot实时应用程序性能监视Apr 13, 2025 am 11:40 AM介绍 在当今快节奏的软件开发环境中,确保最佳应用程序性能至关重要。监视实时指标,例如响应时间,错误率和资源利用率可以帮助MAIN
 Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt击中了10亿用户? Openai首席执行官说:'短短几周内翻了一番Apr 13, 2025 am 11:23 AM“您有几个用户?”他扮演。 阿尔特曼回答说:“我认为我们上次说的是每周5亿个活跃者,而且它正在迅速增长。” “你告诉我,就像在短短几周内翻了一番,”安德森继续说道。 “我说那个私人
 pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一个多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介绍 Mistral发布了其第一个多模式模型,即Pixtral-12b-2409。该模型建立在Mistral的120亿参数Nemo 12B之上。是什么设置了该模型?现在可以拍摄图像和Tex
 生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
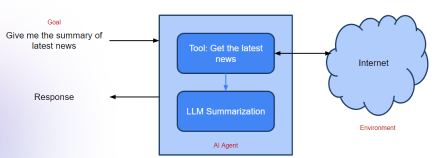
生成AI应用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想象一下,拥有一个由AI驱动的助手,不仅可以响应您的查询,还可以自主收集信息,执行任务甚至处理多种类型的数据(TEXT,图像和代码)。听起来有未来派?在这个a


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

MinGW - 适用于 Windows 的极简 GNU
这个项目正在迁移到osdn.net/projects/mingw的过程中,你可以继续在那里关注我们。MinGW:GNU编译器集合(GCC)的本地Windows移植版本,可自由分发的导入库和用于构建本地Windows应用程序的头文件;包括对MSVC运行时的扩展,以支持C99功能。MinGW的所有软件都可以在64位Windows平台上运行。

螳螂BT
Mantis是一个易于部署的基于Web的缺陷跟踪工具,用于帮助产品缺陷跟踪。它需要PHP、MySQL和一个Web服务器。请查看我们的演示和托管服务。

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用