详解JavaScript中怎么实现队列结构

本篇文章带大家了解一下队列数据结构，详细介绍一下其具有的操作以及在JavaScript中实现队列结构的方法。有一定的参考价值，有需要的朋友可以参考一下，希望对大家有所帮助。

1. 队列数据结构

队列是一种“先入先出”（FIFO）数据结构的类型。第一个入队项目（输入）是第一个出队（输出）。

队列有2个指针：头和尾。队列中的最早排队的项目是在头部，而最新排队的项目在队列尾部。

队列就像我们在地铁排队，靠近车门处的乘客位于队伍的头部，刚进入队伍的乘客位于队伍的尾部。

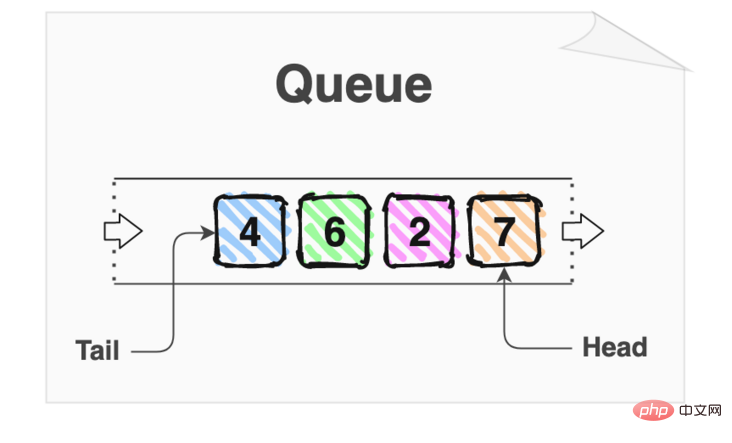
从更高的角度来看，队列是一种数据结构，可以让我们按照入库的顺序依次处理数据的每一项。

2. 队列的操作

队列支持 2 个主要操作：入队（enqueue）和出队（dequeue），另外还有 peek 和 length 操作。

2.1 入队操作

入队操作在队列的尾部插入项目，使其成为队列的队尾。

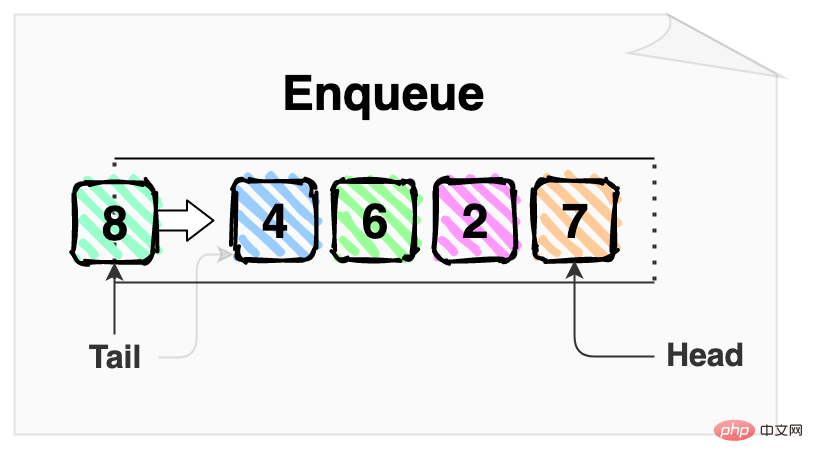
上图中的入队操作在队尾插入了 8，之后 8 成为队列的队尾。

queue.enqueue(8);

2.2 出队操作

出队操作取出队列中第一个项目，此时队列中的下一个项目成为队首。

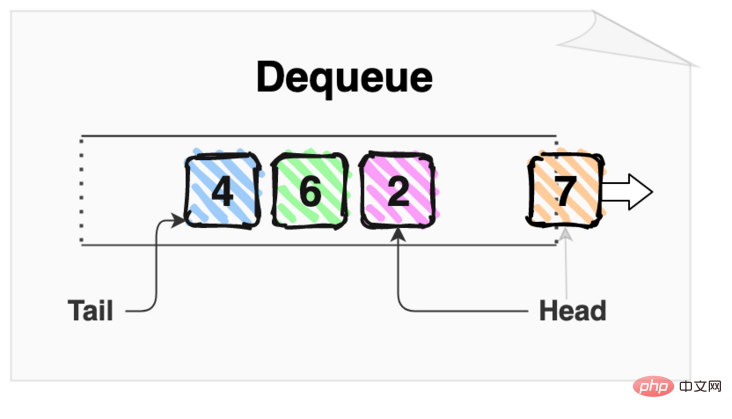
在上图中，出队操作返回项目7并从队列中删除。 出队之后之后，项目 2 成为新的队首。

queue.dequeue(); // => 7

2.3 Peek 操作

Peek 操作读取队首的项目，但是不改变队列。

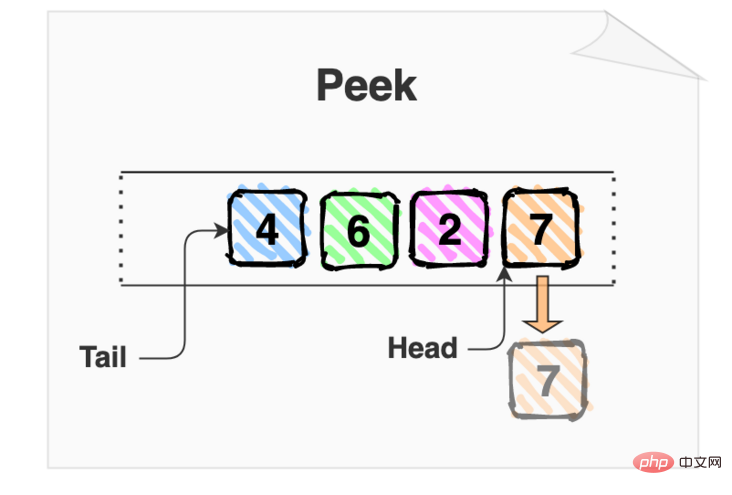
上图中  7 是队首。 peek 操作只需返回队首 7 但是不修改队列。

queue.peek(); // => 7

2.4 length

length 操作返回队列中包含项目的数量。

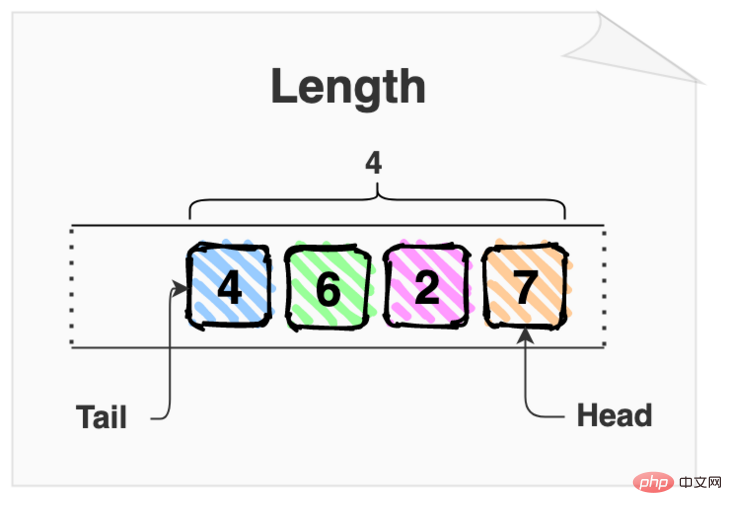
上图中的队列有 4 项：4、6、2 和。7。结果队列长度为 4。

queue.length; // => 4

2.5 队列操作的时间复杂度

关于队列所有操作的重点：enqueue，dequeue，peek 和 length 必须以常数时间复杂度 O(1) 执行。

常数时间复杂度 O(1) 意味着无论队列大小如何（不管是有 10 个还是 100 万个项目），这些操作都必须在相对一致的时间内执行。

3. 用 JavaScript 实现队列

来看一下怎样在保证所有操作必须以常数时间复杂度O(1) 要求实现队列这种数据结构。

class Queue {
  constructor() {
    this.items = {};
    this.headIndex = 0;
    this.tailIndex = 0;
  }

  enqueue(item) {
    this.items[this.tailIndex] = item;
    this.tailIndex++;
  }

  dequeue() {
    const item = this.items[this.headIndex];
    delete this.items[this.headIndex];
    this.headIndex++;
    return item;
  }

  peek() {
    return this.items[this.headIndex];
  }

  get length() {
    return this.tailIndex - this.headIndex;
  }
}

const queue = new Queue();

queue.enqueue(7);
queue.enqueue(2);
queue.enqueue(6);
queue.enqueue(4);

queue.dequeue(); // => 7

queue.peek();    // => 2

queue.length;    // => 3

const queue = new Queue() 是创建队列的实例。

queue.enqueue(7) 方法将 7 存入队列中。

queue.dequeue() 从队列中取出一个头部项目，而 queue.peek() 只读队首项。

最后的 Queue.Length 显示队列中还有多少个项目。

关于实现：在 Queue 类中，普通对象  this.Items  将队列的项目通过数值索引保持。 队首项的索引由 Where.HeadInex 跟踪，队尾项由 this.tailIndex 跟踪。

队列方法的复杂度

在 Queue 的 queue()、 dequeue()、 peek() 和 length() 方法中存在：

• 属性访问器（如:this.items[this.headIndex]），
• 执行算数操作（如:this.headidex++）

这些方法的时间复杂度是恒定的时间 O(1)。

4. 总结

队列是一种遵循先入先出（FIFO）规则的的数据结构。

队列有 2 个主要操作：入队和出队。 另外，队列可以有辅助操作，例如 peek 和 length。

所有队列操作都必须以常数时间 O(1) 执行。

挑战一下：改进 dequeue() 和 peek() 方法，当在空队列上执行时会抛出错误。

更多编程相关知识，请访问：编程入门！！

以上是详解JavaScript中怎么实现队列结构的详细内容。更多信息请关注PHP中文网其他相关文章！