学习Python解决高等数学问题

Python解决高等数学问题，妈妈再也不用担心我的学习

---

使用Python解决高等数学中极限、导数、偏导数、定积分、不定积分、双重积分等问题

Sympy是一个Python的科学计算库，它旨在成为功能齐全的计算机代数系统。 SymPy 包括从基本符号算术到微积分，代数，离散数学和量子物理学的功能。 它可以在 LaTeX 中显示结果。

Sympy官网

文章目录

• Python解决高等数学问题，妈妈再也不用担心我的学习
• 1. 实用技巧
• • 1.1 符号函数
  • 1.2 展开表达式expand
  • 1.3 泰勒展开公式series
  • 1.4 符号展开
• 2. 求极限limit
• 3. 求导diff
• • 3.1 一元函数
  • 3.2 多元函数
• 4. 积分integrate
• • 4.1 定积分
  • 4.2 不定积分
  • 4.3 双重积分
• 5. 求解方程组solve
• 6. 计算求和式summation

（免费学习推荐：python视频教程）

看到这图，是不是感觉快喘不过气了呢。Python来帮你解决。

from sympy import *import sympy

输入“x= symbols(“x”)”命令定义一个符号

x = Symbol("x")y = Symbol("y")

1. 实用技巧

1.1 符号函数

sympy提供了很多数学符号，总结如下

• 虚数单位

sympy.I

• 自然对数

sympy.E

• 无穷大

sympy.oo

• 圆周率

 sympy.pi

• 求n次方根

 sympy.root(8,3)

• 取对数

sympy.log(1024,2)

• 求阶乘

sympy.factorial(4)

• 三角函数

sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)

1.2 展开表达式expand

f = (1+x)**3expand(f)

$x^3+3x^2+3x+1$

1.3 泰勒展开公式series

ln(1+x).series(x,0,4)

$x-\frac{x^2}{2}+\frac{x^3}{3}+O\left(x^4\right)$

sin(x).series(x,0,8)

$x-\frac{x^3}{6}+\frac{x^5}{120}-\frac{x^7}{5040}+O\left(x^8\right)$

cos(x).series(x,0,9)

$1-\frac{x^2}{2}+\frac{x^4}{24}-\frac{x^6}{720}+\frac{x^8}{40320}+O\left(x^9\right)$

(1/(1+x)).series(x,0,5)

$1-x+x^2-x^3+x^4+O\left(x^5\right)$

tan(x).series(x,0,4)

$x+\frac{x^3}{3}+O\left(x^4\right)$

(1/(1-x)).series(x,0,4)

$1+x+x^2+x^3+O\left(x^4\right)$

(1/(1+x)).series(x,0,4)

$1-x+x^2-x^3+O\left(x^4\right)$

1.4 符号展开

a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)

$x^{a+b}$

2. 求极限limit

limit(sin(x)/x,x,0)

$1$

f2=(1+x)**(1/x)

f2

${\left(x+1\right)}^{\frac{1}{x}}$

重要极限

f1=sin(x)/x
f2=(1+x)**(1/x)f3=(1+1/x)**x
lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)

1 E E

dir可以表示极限的趋近方向

f4 = (1+exp(1/x))f4

$e^{\frac{1}{x}}+1$

lim4 = limit(f4,x,0,dir="-")lim4

$1$

lim5 = limit(f4,x,0,dir="+")lim5

$\infty$

3. 求导diff

diff(函数,自变量,求导次数)

3.1 一元函数

求导问题

diff(sin(2*x),x)

$2\cos \left(2x\right)$

diff(ln(x),x)

$\frac{1}{x}$

3.2 多元函数

求偏导问题

diff(sin(x*y),x,y)

$-xy\sin \left(xy\right)+\cos \left(xy\right)$

4. 积分integrate

4.1 定积分

• 函数的定积分: integrate(函数，(变量，下限，上限))
• 函数的不定积分: integrate(函数,变量)

f = x**2 + 1integrate(f,(x,-1.1))

$-1.54366666666667$

integrate(exp(x),(x,-oo,0))

$1$

4.2 不定积分

f = 1/(1+x*x)integrate(f,x)

$\mathrm{atan}\left(x\right)$

4.3 双重积分

f = (4/3)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))

$11.6666666666667$

5. 求解方程组solve

#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])

{x: -1, y: 4}

6. 计算求和式summation

计算求和式可以使用sympy.summation函数，其函数原型为sympy.summation(f, *symbols, **kwargs)

**

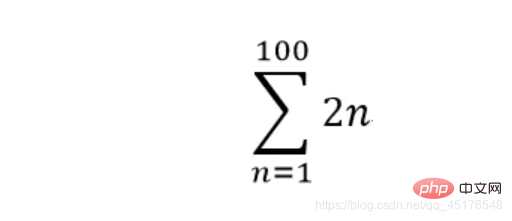
sympy.summation(2 * n,(n,1,100))

10100

到这里就结束了，如果对你有帮助，欢迎点赞关注评论，你的点赞对我很重要。在此也祝愿大家可以把数学学好

相关免费学习推荐：python教程（视频）

以上是学习Python解决高等数学问题的详细内容。更多信息请关注PHP中文网其他相关文章！