深入浅析JavaScript中的快速排序

介绍

排序是指以特定顺序（数字或字母）排列线性表的元素。排序通常与搜索一起配合使用。

有许多排序算法，而迄今为止最快的算法之一是快速排序（Quicksort）。

快速排序用分治策略对给定的列表元素进行排序。这意味着算法将问题分解为子问题，直到子问题变得足够简单可以直接解决为止。

从算法上讲，这可以用递归或循环实现。但是对于这个问题，用递归法更为自然。

了解快速排序背后的逻辑

先看一下快速排序的工作原理：

1. 在数组中选择一个元素，这个元素被称为基准（Pivot）。通常把数组中的第一个或最后一个元素作为基准。
2. 然后，重新排列数组的元素，以使基准左侧的有元素都小于基准，而右侧的所有元素都大于基准。这一步称为分区。如果一个元素等于基准，那么在哪一侧都无关紧要。
3. 针对基准的左侧和右侧分别重复这一过程，直到对数组完成排序。

接下来通过一个例子理解这些步骤。假设有一个含有未排序元素 [7, -2, 4, 1, 6, 5, 0, -4, 2] 的数组。选择最后一个元素作为基准。数组的分解步骤如下图所示：

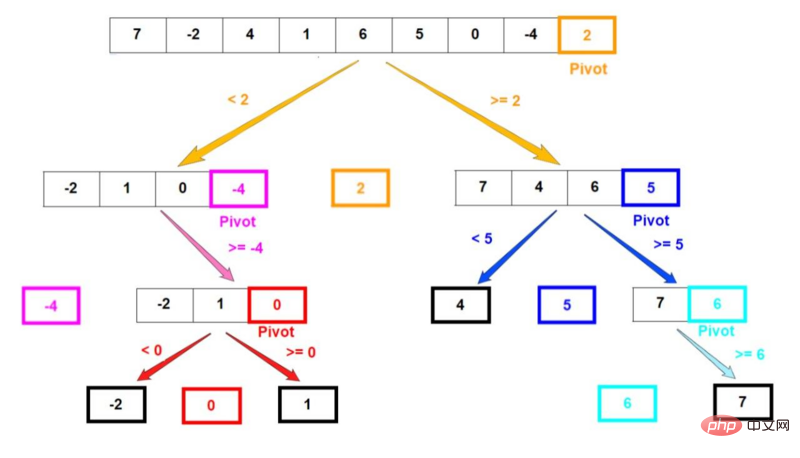
在算法的步骤1中被选为基准的元素带颜色。分区后，基准元素始终处于数组中的正确位置。

黑色粗体边框的数组表示该特定递归分支结束时的样子，最后得到的数组只包含一个元素。

最后可以看到该算法的结果排序。

用 JavaScript 实现快速排序

这一算法的主干是“分区”步骤。无论用递归还是循环的方法，这个步骤都是一样的。

正是因为这个特点，首先编写为数组分区的代码 partition()：

function partition(arr, start, end){
    // 以最后一个元素为基准
    const pivotValue = arr[end];
    let pivotIndex = start; 
    for (let i = start; i < end; i++) {
        if (arr[i] < pivotValue) {
        // 交换元素
        [arr[i], arr[pivotIndex]] = [arr[pivotIndex], arr[i]];
        // 移动到下一个元素
        pivotIndex++;
        }
    }
    
    // 把基准值放在中间
    [arr[pivotIndex], arr[end]] = [arr[end], arr[pivotIndex]] 
    return pivotIndex;
};

代码以最后一个元素为基准，用变量 pivotIndex 来跟踪“中间”位置，这个位置左侧的所有元素都比 pivotValue 小，而右侧的元素都比 pivotValue 大。

最后一步把基准（最后一个元素）与 pivotIndex 交换。

递归实现

在实现了 partition() 函数之后，我们必须递归地解决这个问题，并应用分区逻辑以完成其余步骤：

function quickSortRecursive(arr, start, end) {
    // 终止条件
    if (start >= end) {
        return;
    }
    
    // 返回 pivotIndex
    let index = partition(arr, start, end);
    
    // 将相同的逻辑递归地用于左右子数组
    quickSort(arr, start, index - 1);
    quickSort(arr, index + 1, end);
}

在这个函数中首先对数组进行分区，之后对左右两个子数组进行分区。只要这个函数收到一个不为空或有多个元素的数组，则将重复该过程。

空数组和仅包含一个元素的数组被视为已排序。

最后用下面的例子进行测试：

array = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortRecursive(array, 0, array.length - 1)

console.log(array)

输出：

-4,-2,0,1,2,4,5,6,7

循环实现

快速排序的递归方法更加直观。但是用循环实现快速排序是一个相对常见的面试题。

与大多数的递归到循环的转换方案一样，最先想到的是用栈来模拟递归调用。这样做可以重用一些我们熟悉的递归逻辑，并在循环中使用。

我们需要一种跟踪剩下的未排序子数组的方法。一种方法是简单地把“成对”的元素保留在堆栈中，用来表示给定未排序子数组的 start 和 end。

JavaScript 没有显式的栈数据结构，但是数组支持 push() 和 pop() 函数。但是不支持 peek()函数，所以必须用 stack [stack.length-1] 手动检查栈顶。

我们将使用与递归方法相同的“分区”功能。看看如何编写Quicksort部分：

function quickSortIterative(arr) {
    // 用push()和pop()函数创建一个将作为栈使用的数组
    stack = [];
    
    // 将整个初始数组做为“未排序的子数组”
    stack.push(0);
    stack.push(arr.length - 1);
    
    // 没有显式的peek()函数
    // 只要存在未排序的子数组，就重复循环
    while(stack[stack.length - 1] >= 0){
        
        // 提取顶部未排序的子数组
        end = stack.pop();
        start = stack.pop();
        
        pivotIndex = partition(arr, start, end);
        
        // 如果基准的左侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex - 1 > start){
            stack.push(start);
            stack.push(pivotIndex - 1);
        }
        
        // 如果基准的右侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex + 1 < end){
            stack.push(pivotIndex + 1);
            stack.push(end);
        }
    }
}

以下是测试代码：

ourArray = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortIterative(ourArray)

console.log(ourArray)

输出：

-4,-2,0,1,2,4,5,6,7

可视化演示

当涉及到排序算法时，将其可视化能帮我们直观的了解它们是怎样运作的，下面这个例子搬运自维基百科：

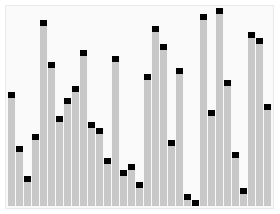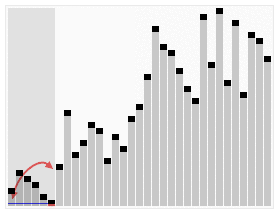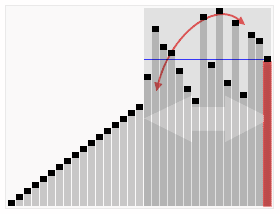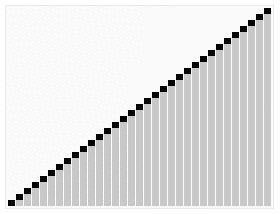
在图中也把最后一个元素作为基准。给定数组分区后，递归遍历左侧，直到将其完全排序为止。然后对右侧进行排序。

快速排序的效率

现在讨论它的时间和空间复杂度。快速排序在最坏情况下的时间复杂度是 $O(n^2)$。平均时间复杂度为 $O(n\log n)$。通常，使用随机版本的快速排序可以避免最坏的情况。

快速排序算法的弱点是基准的选择。每选择一次错误的基准（大于或小于大多数元素的基准）都会带来最坏的时间复杂度。在重复选择基准时，如果元素值小于或大于该元素的基准时，时间复杂度为 $O(n\log n)$。

根据经验可以观察到，无论采用哪种数据基准选择策略，快速排序的时间复杂度都倾向于具有 $O(n\log n)$ 。

快速排序不会占用任何额外的空间（不包括为递归调用保留的空间）。这种算法被称为in-place算法，不需要额外的空间。

更多编程相关知识，请访问：编程入门！！

以上是深入浅析JavaScript中的快速排序的详细内容。更多信息请关注PHP中文网其他相关文章！